3.4 正 规 式 与 有 穷 自 动 机

正 规 式 与 有 穷 自 动 机

有穷自动机是具有离散输入与输出系统的一种抽象数学模型。有穷自动机有“确定的”和“非确定的”两类,确定的有穷自动机和非确定的有穷自动机都能准确地识别正规集。

确定有穷自动机( DFA )

一个确定有穷自动机 M 是一个五元组 M = ( Q ,Σ , f , S , Z ),其中
Q 是一个有穷状态集合,每一个元素称为一个状态;
Σ 是一个有穷输入字母表,每个元素称为一个输入字符;
f 是一个从 Q × Σ 到 Q 的单值映射,
f ( q i , a ) = q j ( q i , q j ∈ Q , a ∈ Σ )

表示当前状态为 qi ,输入字符为 a 时,自动机将转换到下一个状态 q j ,q j 称为 q i 的一个后继状态。我们说状态转换函数是单值函数,是指f ( q i , a )唯一地确定了下一个要转移的状态,即每个状态的所有输出边上标记的输入字符不同,如图 3.2 所示。

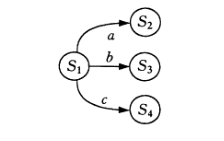
图 3.2 S 1 的状态转换

由图可知:

f ( S 1 , a ) = S 2
 f ( S 1 , b ) = S 3 
 f ( S 1 , c ) = S 4

是单值映射函数。
S ∈ Q 是唯一的一个初态;
Z ⊆ Q 是一个终态集。

【例 3.10 】
设 DFA M = ({ q 0 , q 1 , q 2 },{ a , b }, f , q 0 ,{ q 2 }),其中

f ( q 0 , a ) = q 1			 f ( q 1 , b ) = q 1
f ( q 0 , b ) = q 2			 f ( q 2 , a ) = q 2
f ( q 1 , a ) = q 1			 f ( q 2 , b ) = q 1

一个 DFA 可用一个矩阵表示,该矩阵的行表示状态,列表示输入符号,矩阵元素表示f ( q , a )的值,该矩阵称为状态转换矩阵,或称转换表。例 3.10 中 DFA M 所对应的状态转换矩
阵如表 3.1 所示。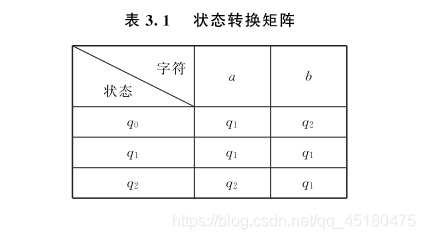

一个 DFA 也可以表示成一张状态转换图。假定 DFA M 有 m 个状态,n 个输入字符,那么这个状态转换图含有 m 个状态结,每个状态结最多有 n 条箭弧射出和别的状态结相连接,每条弧用 Σ中的一个不同的输入字符作标记。整个图含有唯一一个初态结和若干个终态结。

例 3.10 中 DFA M 的状态转换图如图 3.3 所示。

对 Σ * 中的任何符号串 β ,若存在一条从初态结到终态结的道路,而且在这条路上所有弧的标记连接成的符号串等于 β ,则称 β 为 DFA M 所识别(或接受),若 M 的初态结同时又是终态结,则 ε 可为 M 所识别。 DFA M 所识别的符号串的全体记为 L ( M ),称为 DFA M 所识别的语言。例 3.10 的 DFA M 所识别的语言为 L ( M ) = ba * 。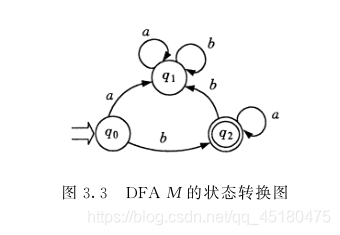
非确定有穷自动机( NFA )

一个非确定有穷自动机 M 是一个五元组 M = ( Q ,Σ , f , S , Z ),其中 Q , Σ , Z 意义同 DFA ,f 和 S 不同于 DFA 。

状态转换函数 f 不是单值函数,它是一个多值函数。f ( q i , a ) = {某些状态的集合}( q i ∈ Q ),表示不能由当前状态、当前输入字符唯一地确定下一个要转移的状态,即允许同一个状态对同一输入字符有不同的输出
边,如图 3.4 所示。

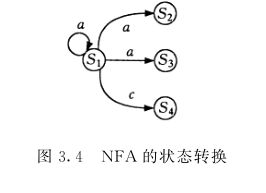
图 3.4 NFA 的状态转换

由图 3.4 可知,
f ( S 1 , a ) = { S 1 , S 2 , S 3 },即 f 是一个从 Q × Σ * 到 Q 的子集的映射。非确定的有穷自动机还允许 f (q i , ε ) = {某些状态的集合},就是说,在 NFA 的状态转换图中,边上的标记可以是 ε 。
S ⊂ Q 是非空初态集。

【例 3.11 】设有 NFA M’ = ({ 1 , 2 , 3 },{ a , b }, f ,{ 1 , 3 },{ 2 }),其中

f ( 1 , a ) = { 3 } 	 f ( 2 , a ) = Ø     	f ( 3 , a ) = Ø
f ( 1 , b ) = { 1 , 2 }	 f ( 2 , b ) = { 3 }	 f ( 3 , b ) = { 2 }

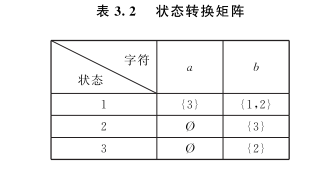
同 DFA 一样,一个 NFA 也可以用一个矩阵或一张状态转换图表示。例中 NFA M’ 所对应的状态转换矩阵如表 3.2 所示。

例 3.11 中 NFA M’ 对应的状态转换图如图 3.5 所示。

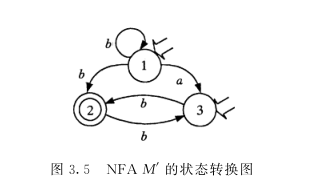
对于 Σ * 中的任何一个符号串 β ,若存在一条从初态结到某一终态结的道路,且这条路上所有弧的标记依次连接成的字符串等于 β ,则称 β 可为 NFA M’ 所识别。若 M’ 的某些结既是初态结又是终态结,或者存在一条从初态结到终态结的 ε 道路,那么 ε 可为 M’ 所接受。 NFA M’所接受 Σ * 中字符串的集合称为 NFA M’ 所识别的语言,记为 L ( M’ )。例 3.11 中 NFA M’ 所识
别的语言为 L ( M’ ) = b* (b | ab )( bb )* 。

由 NFA 的定义可知,同一个符号串 β 可由多条路来识别,例 3.11 中 NFA M’ ,对符号串 β = bbb 可由 3 条路来识别。第 1 条路:状态 1→ 状态 2→ 状态 3→ 状态 2 ;第 2 条路:状态 1→ 状态 1→ 状态 2 ;第 3 条路:状态 3→ 状态 2→ 状态 3→ 状态 2 。这样,对于非确定的有穷自动机,难以用计算机程序来模拟,作为描述控制过程的自动机,通常都是确定的有穷自动机。事实上,显然 DFA 是 NFA 的特例。另外,可以通过数学归纳法证明,对于每个 NFA M 存在 DFA M’ ,使 L ( M ) = L ( M’ ),因此,我们利用有穷自动机构造词法分析程序的方法是从语言单词的描述中构造出非确定的有穷自动机,再将非确定的有穷自动机转化为确定的有穷自动机,并将其化简为状态最少化的 DFA ,然后对 DFA 的每一个状态构造一小段程序将其转化为识别语言单词的词法分析程序。下面将讨论如何从描述语言单词的正规式中构造出识别其语言单词的有穷自动机。

由正规表达式 R 构造 NFA

输入:字母表 Σ 上的正规式 R 。
输出:识别(接受)语言 L ( R )的 NFA N 。

方法:
(1 )引进初始结点 X 和终止结点 Y ,把 R 表示成拓广转换图,如图 3.6 所示。

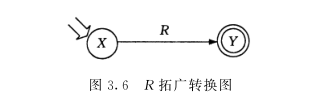
(2 )分析 R 的语法结构,用如下规则对 R 中的每个基本符号构造 NFA 。
① R = Ø ,构造 NFA ,如图 3.7 所示。

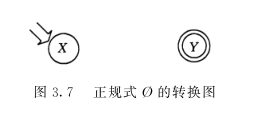
② R = ε ,构造 NFA ,如图 3.8 所示。

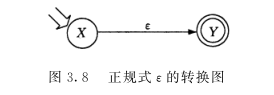
③ R = a ( a ∈ Σ ),构造 NFA ,如图 3.9 所示。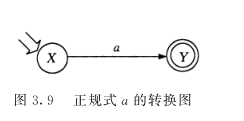
④ 若 R 是复合正规式,则按图 3.10 的转换规则对 R 进行分裂和加进新结,直至每个边上只留下一个符号(或 ε )为止。

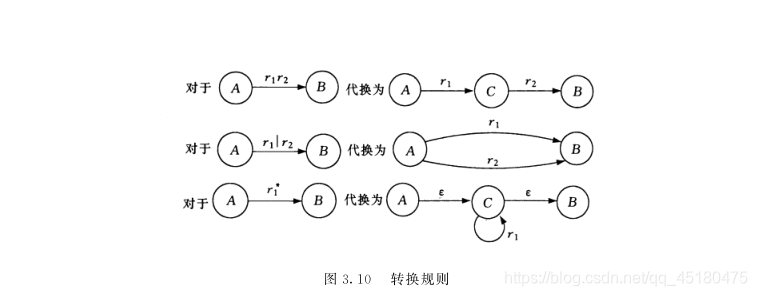
(3 )整个分裂过程中,所有新结均采用不同的名字,保留 X , Y 为全图唯一初态结和终态结。

【例 3.12 】试构造识别语言 R = ( a | b )* abb 的NFA N ,使 L ( N ) = L ( R )。首先将 R 表示成如图 3.11 所示的拓广转换图。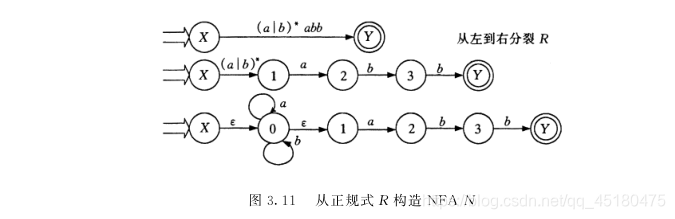
【例 3.13 】试构造识别标识符的 NFA ,描述标识符的正规式 R = l ( l | d )* 。首先将 R 表示成如图 3.12 所示的拓广转换图。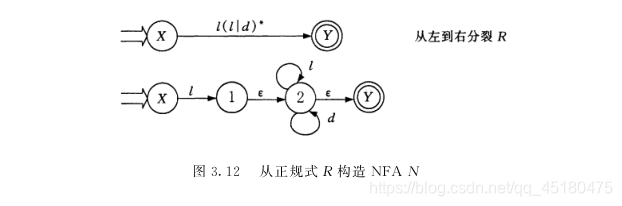
NFA 确定化为 DFA 的方法

见下一节