计算机软件技术实习日志项目一(二) 简易计算器项目实现
文章目录
前言
大家好,我将为大家介绍我实现计算器的具体细节,做软件是我之前没有接触过的领域,做得不好,大家不要见怪。本篇文章着重介绍简易计算器功能的实现,原理部分的知识请结合《计算机软件技术实习日志项目一(一) 简易计算器项目准备》观看。本文暂时只对主要功能进行讲解不会贴上所有代码,不过我已经贴上了参考资料,大家可以自行学习。
一、软件安装及创建项目
大家可以参考以下连接
https://blog.youkuaiyun.com/Mrweng1996/article/details/103202297
二、参数定义
主要罗列了一些我自己定义的参数。
部分函数将在后面单讲
对话框头文件:
//对话框类内
private:
CString exstr;
CString restr;
CString h1, h2, h3, h4, h5, h6;
public:
//数字
afx_msg void OnBnClickedone();
afx_msg void OnBnClickedtwo();
afx_msg void OnBnClickedthree();
afx_msg void OnBnClickedfour();
afx_msg void OnBnClickedfive();
afx_msg void OnBnClickedsix();
afx_msg void OnBnClickedseven();
afx_msg void OnBnClickedeight();
afx_msg void OnBnClickednine();
afx_msg void OnBnClickedzero();
//运算符
afx_msg void OnBnClickedadd();
afx_msg void OnBnClickedsub();
afx_msg void OnBnClickedmul();
afx_msg void OnBnClickeddiv();
afx_msg void OnBnClickedequ();
afx_msg void OnBnClickedleft();
afx_msg void OnBnClickedright();
afx_msg void OnBnClickeddot();
//其他
afx_msg void OnBnClickedback(); //删除
afx_msg void OnBnClickedclear();//清空表达式框
afx_msg void OnEnChangeex(); //空函数
afx_msg void OnEnChangeres(); //空函数
afx_msg void OnBnClickedclearall(); //清空历史
//对话框类外
void behind(); //中缀转后缀表达式
double caculator(); //二叉树运算后缀表达式,该函数为空,我写在等于号的控件函数里了
void init(); //参数初始化
对话框源文件:
CONST INT maxn = 1000;
CONST INT maxop = 10;
/*
无论是数还是运算符用,结点结构体统一代表。
用flag区分,1代表数,2代表符号
*/
struct node {
INT flag;
double num;
CHAR opc;
node() {
}
node(INT f, double nu) {
flag = f, num = nu;
opc = '\0';
}
node(INT f, CHAR c) {
flag = f, num = 0;
opc = c;
}
};
/*
二叉树利用链式向前星表示
*/
INT head[maxn + 10], hcnt, root, ncnt;
node tnode[maxn + 10];
struct Edge {
int v, next;
}edge[maxn * 2 + 10];
VOID addedge(INT u, INT v) {
edge[++hcnt].v = v, edge[hcnt].next = head[u], head[u] = hcnt;
}
/*
一开始不会在MFC用STL,于是自定义了栈和队列
*/
struct stackc {
CHAR sc[maxn + 10];
int cnt;
stackc() {
cnt = 0;
}
void push(char c) {
sc[++cnt] = c;
}
void pop() {
--cnt;
}
int size() {
return cnt;
}
CHAR top() {
return sc[cnt];
}
BOOL empty() {
return cnt == 0;
}
};
struct stacki {
double si[maxn + 10];
INT cnt;
stacki() {
cnt = 0;
}
void push(INT c) {
si[++cnt] = c;
}
void pop() {
--cnt;
}
int size() {
return cnt;
}
double top() {
return si[cnt];
}
BOOL empty() {
return cnt == 0;
}
};
struct queuen {
node qn[maxn + 10];
INT h, t;
queuen() {
h = t = 1;
}
void push(node c) {
qn[t] = c;
++t;
}
void pop() {
++h;
}
int size() {
return t - h;
}
node front() {
return qn[h];
}
BOOL empty() {
return (t - h) <= 0;
}
};
INT nop = 7; //运算符种类
INT cm[7][7] = { 1,1,-1,-1,-1,1,1, //优先级比较数组
1,1,-1,-1,-1,1,1,
1,1,1,1,-1,1,1,
1,1,1,1,-1,1,1,
-1,-1,-1,-1,-1,0,2,
1,1,1,1,2,1,1,
-1,-1,-1,-1,-1,2,0
};
CHAR s[maxn + 10]; //接受exstr
CHAR op[maxop] = { '+','-','*','/','(',')','#' };
map<CHAR, INT> id; //利用map使得运算符对应上序号
stackc opstack; //生成后缀表达式的时候用的操作符栈
queuen postqueue; //生成后缀表达式的时候用的结点队列
stacki binstack; //二叉树运算时用的栈
BOOL isnum(CHAR c) { //判断是否为数字
return c >= '0' && c <= '9';
}
double getnum(INT& st, INT lim) { //获得数字
long long res = 0;
long long div = 1;
bool is_dot=0;
for (; (isnum(s[st])||s[st]=='.') && (st <= lim); ++st) { //读到小数点不终止判断
if (s[st] == '.') {
is_dot = 1;
if (!(isnum(s[st + 1]) || s[st + 1] == '.')) {
break;
}
continue;
}
if (is_dot) { //小数点后每有一位就乘10;
div *= 10;
}
res = res * 10 + s[st] - '0';
if (!(isnum(s[st + 1])||s[st+1]=='.')) {
break;
}
}
return 1.0*res/div; //相当于先按照整数读取,然后再除10...0
}
void init() { //初始化参数
for (INT i = 0; i < nop; ++i) {
id[op[i]] = i;
}
memset(s, 0, sizeof s);
opstack.cnt = hcnt=root=ncnt=0;
memset(opstack.sc, 0, sizeof opstack.sc);
memset(tnode, 0, sizeof tnode);
memset(edge, 0, sizeof edge);
}
二、添加计算器按键键
1.数字键
在对话框上添加一个Button,然后在属性栏进行相关编辑,然后双击Button键,我们就可以在自动生成的函数例进行编程了。
void CcalculatorDlg::OnBnClickedone() //自动生成的
{
// TODO: 在此添加控件通知处理程序代码
UpdateData(TRUE);
exstr = exstr + _T("1"); //在表达是后面加一个1,exstr是我定义的表达式
UpdateData(FALSE);
}
2.运算符键
2.1加号
void CcalculatorDlg::OnBnClickedadd()
{
// TODO: 在此添加控件通知处理程序代码
UpdateData(TRUE);
if (exstr.GetLength()>0&&exstr[exstr.GetAllocLength() - 1] != '+') {
//防止连续的加号或者开头一个加号
exstr = exstr + _T("+");
}
UpdateData(FALSE);
}
2.2小数点
添加小数点是应该注意一下问题:
1.一个数最多有一个小数点
2.直接加小数点代表0.xx,但是不能再有括号后直接加小数点
void CcalculatorDlg::OnBnClickeddot()
{
// TODO: 在此添加控件通知处理程序代码
/*
我首先判断交加小数点的位置之前表达式的情况。
若果是有数字,且其他运算符别小数点先出现,就可以加小数点。
如果前面是除左括号的运算符,那么就加“0.”
*/
UpdateData(TRUE);
bool ok = 1;
bool is_num = 0,is_op=0;
char cop=0;
int cnt = 0;
int pre[10]; //有用的只有下标1和2,因为我只用判断位置前两种字符。
for (int i = exstr.GetLength() - 1; i >= 0; --i) {
if (isnum(exstr[i])) {
if (is_num == 0) { //is_..用于记录是否出现过
pre[++cnt] = 1; //1代表数字出现过。
is_num = 1;
}
}
else{
if (is_op == 0) {
pre[++cnt] = 2; //代表除小数点外的运算符
is_op = 1;
cop = exstr[i]; //记下该运算符
}
}
if (cnt == 2) { //出现两种退出
break;
}
}
if (pre[1] == 1 && ((pre[2] == 2 || is_op == 0)) ){ //正常情况直接加
if(cop!='.')exstr += _T(".");
}
if (pre[1] == 2 ) {
if( cop != ')'&&cop!='.')exstr += _T("0."); //加前导零
}
if (!(is_num || is_op )) { //最开始输入小数点
exstr += _T("0.");
}
UpdateData(FALSE); //其余情况不加
}
2.3等于号
void CcalculatorDlg::OnBnClickedequ()
{
// TODO: 在此添加控件通知处理程序代码
int len = exstr.GetLength();
for (INT i = 0; i < len; ++i) { //使(-...)的情况变为(0-...)
if (exstr[i] == '(' && (exstr[i + 1] == '-'|| exstr[i + 1] == '+')) {
exstr = exstr.Left(i + 1) + _T("0") + exstr.Right(len - i - 1);
len += 1;
}
}
for (INT i = 0; i < len;++i) {
s[i + 1] = exstr[i];
}
behind(); //中缀转后缀
double ans = caculator(); //求值
restr = _T("");
restr.Format(_T("%lf"), ans);
h6 = h5; //更新历史记录
h5 = h4;
h4 = h3;
h3 = h2;
h2 = h1;
h1 = exstr+_T("=")+restr;
exstr = restr = _T("");
init(); //初始化参数
UpdateData(FALSE);
}
3其他键
3.1删除键
删除键相当于只取前length-1个字符
清空键相当于把对应字符串清空,然后更新数据就好。
void CcalculatorDlg::OnBnClickedback()
{
// TODO: 在此添加控件通知处理程序代码
UpdateData(TRUE); //将关联控件的值上传到关联变量上
if (exstr.GetLength()>0) {
exstr = exstr.Left(exstr.GetLength() - 1); //最后一个字符不取
}
UpdateData(FALSE); //将关联变量的值上传到关联控件上
}
三、中缀表达式转后缀表达式
请大家结合上一篇的文章中的中缀转后缀。
void behind() {
INT len = strlen(s + 1);
while (!postqueue.empty()) { //清空
postqueue.pop(); //代表后缀表达式
}
while (!opstack.empty()) { //清空
opstack.pop();
}
for (INT i = 1; i <= len; ++i) { //挨个读取
if (i == 1 && s[i] == '-') { //第一个是负数相当于是存一个0,再存一个减号
postqueue.push(node(1, 0.0));
opstack.push('-');
}
else if (isnum(s[i])) {
postqueue.push(node(1, getnum(i, len)));
}
else {
if (opstack.size() == 0 || s[i] == '(') {
opstack.push(s[i]);
}
else if (s[i] == ')') {
while (opstack.top() != '(') {
postqueue.push(node(2, opstack.top()));
opstack.pop();
}
opstack.pop();
}
else {
while (!opstack.empty() && cm[id[opstack.top()]][id[s[i]]] >= 0) {
postqueue.push(node(2, opstack.top()));
opstack.pop();
}
opstack.push(s[i]);
}
}
}
while (!opstack.empty()) {
postqueue.push(node(2, opstack.top()));
opstack.pop();
}
}
四、利用二叉树计算后缀表达式
请大家结合上一篇文章的用二叉树来求解后缀表达式的值。
double cal(double opd1, CHAR opch, double opd2) { //四则运算
if (opch == '+') return opd1 + opd2;
if (opch == '-') return opd1 - opd2;
if (opch == '*') return opd1 * opd2;
if (opch == '/') return opd1 / opd2;
}
double dfs(INT idx) { //二叉树的深搜
if (tnode[idx].flag == 1) {
return tnode[idx].num;
}
INT idd[3], cnt = 0;
for (INT i = head[idx]; i; i = edge[i].next) {
idd[++cnt] = edge[i].v;
}
return cal(dfs(idd[1]), tnode[idx].opc, dfs(idd[2]));
}
double caculator() { //根据后缀表达式简历二叉树
node tmp;
INT tf = 0;
hcnt = root = ncnt=0;
memset(head, 0, sizeof head);
while (!postqueue.empty()) {
tmp = postqueue.front();
postqueue.pop();
tnode[++ncnt] = tmp;
tf = tmp.flag;
if (tf == 1) {
binstack.push(ncnt);
}
else {
addedge(ncnt, binstack.top());
binstack.pop();
addedge(ncnt, binstack.top());
binstack.pop();
binstack.push(ncnt);
}
if (postqueue.size() == 0) {
root = ncnt;
}
}
return dfs(root);
}
五、演示
1.计算器演示1
2.计算器演示2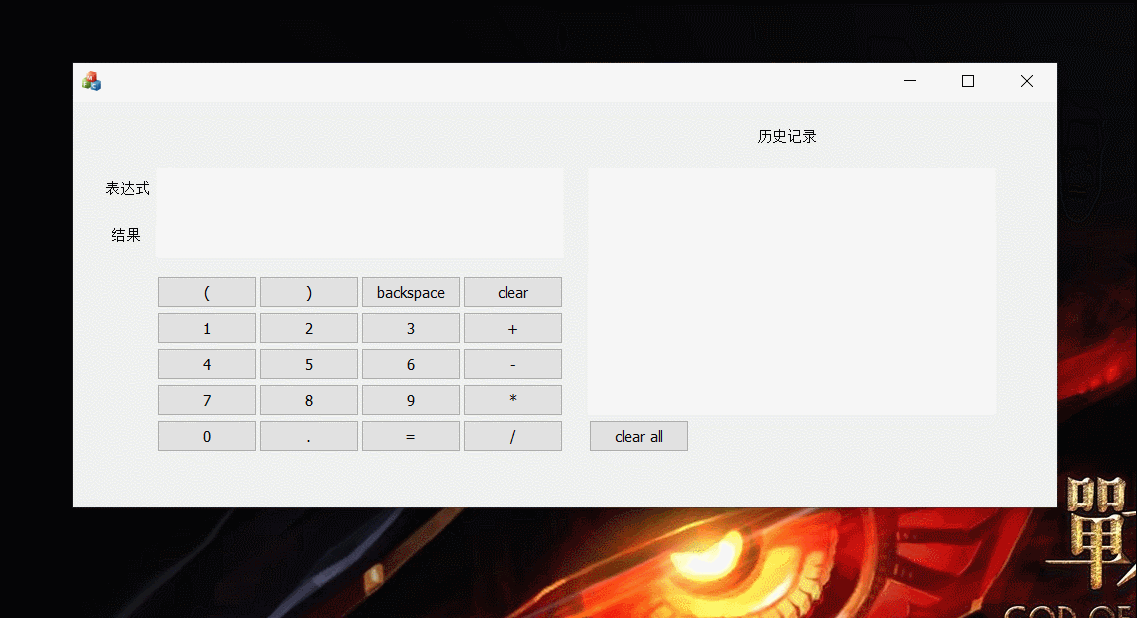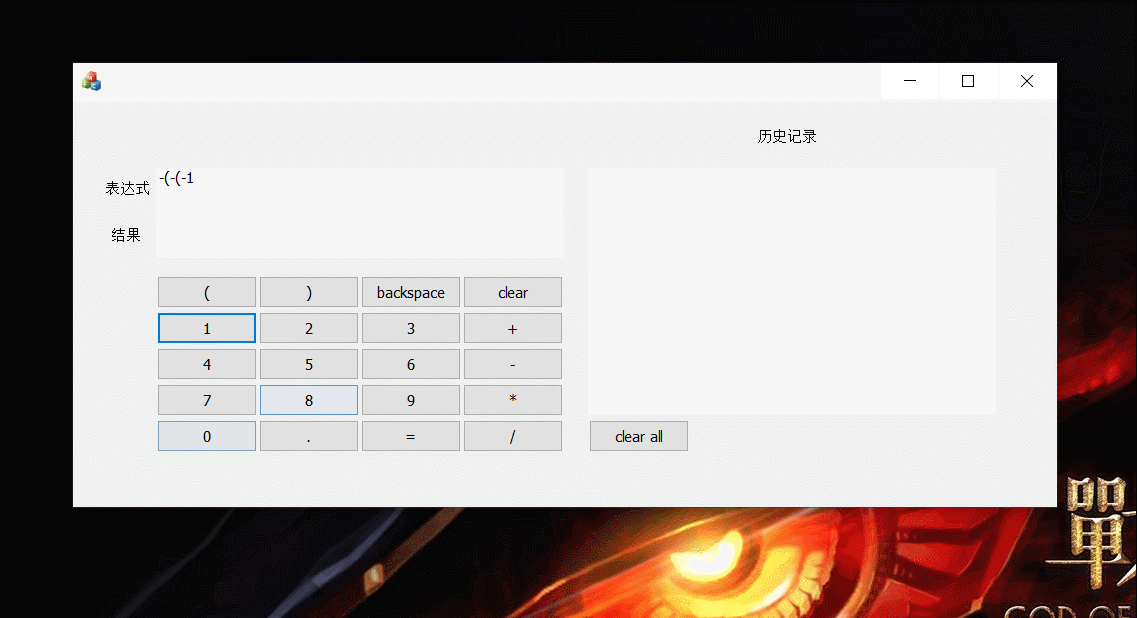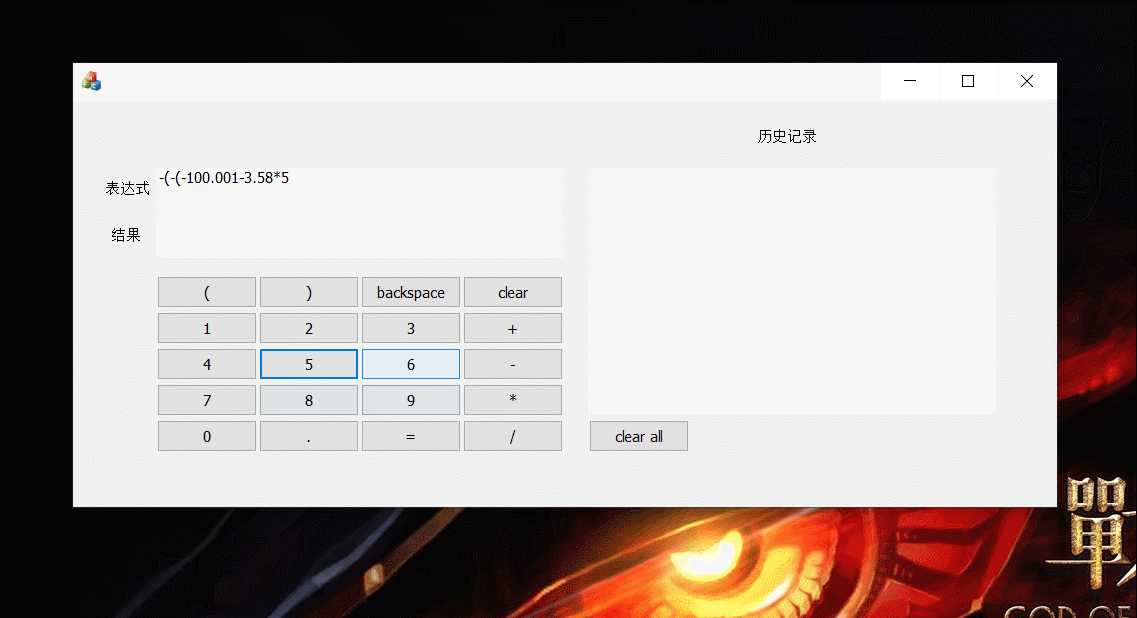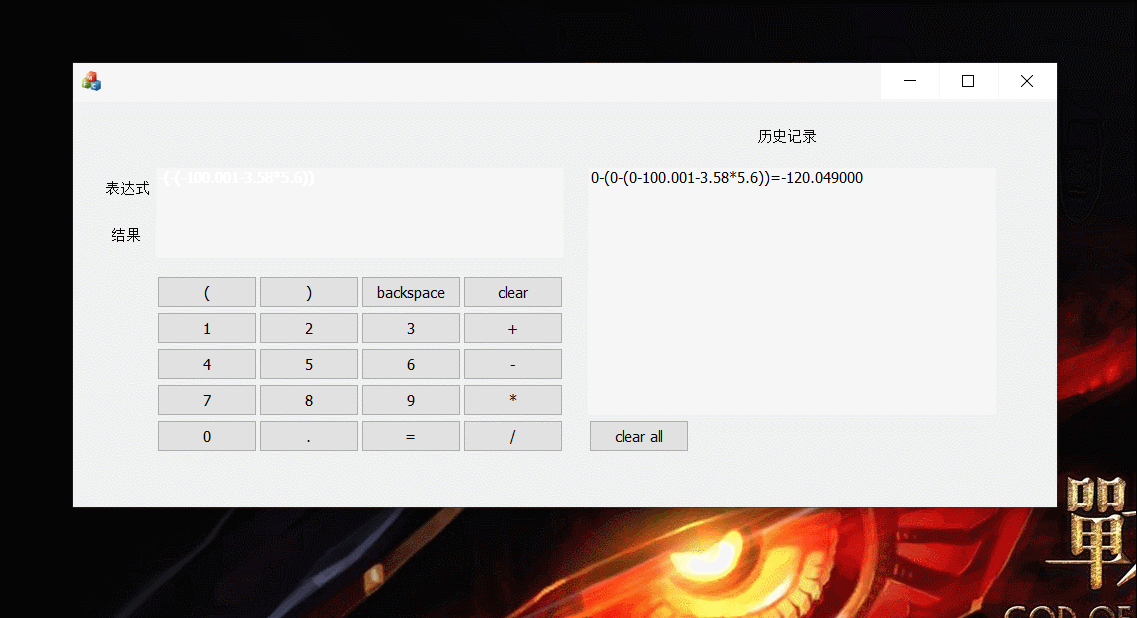
六、总结
这是我第一次用MFC写软件学到了不少,算法方面问题不大,但是MFC调试的时候对我造成了一些影响。我将在接下来的项目中学习更多MFC的使用方法。另外本计算器对于表达式的规范检查尚不完全,还需要完善。
七、参考资料
【1】 B站up主pl-Alex 【MFC】简易计算器的实现(2) https://www.bilibili.com/video/BV1SA411i7Xw/?spm_id_from=333.788.videocard.0
//这资源只能实现简单双目运算,大家需要从我上一篇文章和本篇文章来学习算法方面的知识。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








