最近了解了一下Transformer的基本架构,在这里简单记录一下,加深理解,防止遗忘。如有不正确之处,还请批评指正。
Transformer包含一个Encoder Block和一个Decoder Block。Encoder Block和Decoder Block是由许多具有相同结构的块组,图1为Transformer的基本架构。每个块主要是由多头注意力机制层,前馈神经网络层(FFN),残差连接,以及层归一化(LN)层组成。不同的是,对于decoder,为了保证预测的因果性,采用的是带掩码的多头注意力机制。下面按照顺序详细地描述Transformer的各个组成模块。

词嵌入(word embedding)也就是图中的Input Embedding:我的理解就是将单词转化为向量的形式,转化为计算机可以理解计算的。最直观的方式就是one-hot编码,具体来说,one-hot编码将每个单词映射到一个长度等于词汇表大小的向量,其中只有一个元素为1,其余元素均为0。这个1的位置对应于单词在词汇表中的索引位置。举个例子,假如你有4个单词,那么每个单词编码的维度就是4维,假如第一个单词是apple,就对应0001;第二个单词是banana,就对应0010,以此类推。但是这样的编码方式存在一些局限性,由于one-hot编码只使用一个维度来表示一个单词,因此它会导致高维稀疏矩阵,占用大量的内存空间 。另外,one-hot编码没有考虑单词之间的语义关系,比如苹果和香蕉都是水果,它们之间的距离可能是很接近的,但是one-hot编码无法捕捉到这种相似性。并且one-hot编码无法处理未知的单词。目前,使用较多的是word2vec和GloVe。
位置嵌入(position embedding): 由于自注意力机制的设计,输入序列中的每个词向量都是并行处理的,这也就是说自注意力层缺乏捕捉位置信息的能力。而在一句话中,词汇处在不同的位置,可能会导致句子的意思天差地别。比如,“我欠他100W” 和 “他欠我100W”。因此位置信息是非常重要的。Transformer通过位置编码(Positional Encoding)来为每个词向量添加位置信息,以解决这一问题。原始的Transformer模型中,位置编码是预先计算好的,通常使用正弦和余弦函数来为每个位置生成一个独特的编码,属于是绝对位置编码。后续的swinTransformer中使用了相对位置编码,后续在进行介绍。基于正余弦的编码公式如下

其中pos表示词在句子中的绝对位置,d表示embedding之后向量的维度(后续会将词向量与位置向量相加,所以他们的维度是相同的),处于偶数维度的按照(1.1)进行编码,处于奇数维度的按照(1.2)进行编码。根据三角函数的公式,处在pos位置的单词和处在pos+k位置的单词的位置嵌入是可以相互表示的

也就是说各个位置之间是可以相互计算得到,位置向量中蕴含着相对位置信息。随着技术的发展,位置编码也可以是可训练的,将其作为模型参数的一部分,通过将位置编码作为可学习的参数,模型可以在训练过程中自动调整位置编码。
自注意力机制:将输入的向量矩阵(就是将一句话对应所有单词的向量表示拼成一个矩阵)分别和三个权重矩阵相乘
得到矩阵
。如下图所示。黑色,红色,蓝色分别别是一句话三个单词的对应的向量。它们拼起来组成一个矩阵input。分别和权重矩阵相乘得到矩阵QKV。

下面开始计算注意力:
- 通过计算Q和K的转置,得到不同单词之间的相关性

得到的矩阵第i行第j列的元素,即为第i个单词和第j个单词之间的相关性。
- 根据softmax函数,softmax函数会对每个输入值进行指数运算,然后对所有指数结果进行归一化处理,使得它们的和为1。当输入值之间差异较大时,较大的输入值经过指数运算后会远大于其他值,导致softmax函数输出中该值的概率接近1,而其他值的概率则接近0。在反向传播过程中,计算梯度时会涉及到这些概率值。由于大部分概率值都非常小,根据链式法则,这些小数值在求导过程中相乘会导致梯度变得非常小,从而引起梯度消失现象。为了避免softmax函数梯度消失的问题,在经过softmax函数之前,首先对除以
- 对行这一维度使用softmax函数进行归一化处理,将不同单词之间的相关性转化为概率
- 根据每个单词之间的概率分布,然后乘上对应的Values值。根据矩阵乘法进行理解,做完乘法的第i行其实就是在关注这第i个单词时,所有单词权重的线性组合。

decoder中的交叉注意力机制:
在decoder的多头注意力中与encoder的注意力基本是相同的,不同的是矩阵K和V是来自encoder的输出,Q是来自前面掩码注意力层的输出,形成了一个交叉注意力,交叉注意力可以捕捉到输入的序列和目标序列之间的关系,从而可以更好的预测输出。如下图所示。

带掩码的注意力机制:
对于decoder,训练时的输入是目标序列(训练时是目标序列是已知的),由于使用自注意力(Self-Attention)机制,所有输入信息是并行同时暴露给模型,这就使得模型在训练时可以提前接触到未来的信息,但是在预测时模型的输入是前面已经输出的单词,对于未来单词是不知情的。举个例子,测试时,encoder端输入“I love you”,decoder在预测第一个词是“我”之后,要开始预测第二个词,预测第二个词时只知道前面预测的“我”,不能知道后面的是什么,为了保证因果一致性所以在训练时,就要将未来的词遮住。因此,引入了掩码(Mask)机制,确保在生成当前词的时候,不会受到序列中未来词的影响。实际可以通过生成一个掩码矩阵来实现。
- 首先生成一个上三角矩阵

其中1的位置,表示要遮住的地方。在预测第一个单词的时候,所有的都是不知道的,因此第一行全部为1。在预测第二个单词的时候,第一个单词是已知的,所以第二行第一个位置为0,后面的单词是未知的,所以为1。后面的以此类推。所以可以生成一个大小的上三角矩阵,
表示句子中单词的个数。然后将为1的位置,填充一个负无穷大的数。之后加到上
,因为负无穷大加上一个常数也是负无穷大,所以经过softmax函数归一化处理之后,就会变得无穷小。也就是说,对于未来单词,对它的注意力是0,只对已经预测过的单词计算注意力,保证因果性。
多头注意力机制:将单头的QKV矩阵的M个维度分给H个头去学习,那么每个头Q’,K’, V’的维度。由于训练的随机初始化,不同的头能学到不同的子空间表示。学习后,将不同头的拼在一起,恢复为原来的维度。
其中为投影权重矩阵(通常
)。为了后续的残差连接,需要与input的维度相同,所以一般要进行一个投影。
残差连接:在深度学习中,随着网络层数的增加,梯度消失和梯度爆炸问题变得更加严重,导致网络难以训练。残差网络的设计目的是使网络能够更容易地学习输入与输出之间的恒等映射,从而解决这些问题,下图为残差网络的结构(左)和常规网络结构(右)。

对于常规网络前向传播
对于残差网络前向传播:
对于常规网络的反向传播:
随着网络层数的增加,梯度在反向传播过程中需要经过更多的连乘,这会导致梯度值迅速减小,导致低层网络接收到的梯度接近于零。
对于残差网络反向传播:
由于残差连接,回传的梯度乘积的第二项有一个1存在,避免了在深层网络中梯度的连乘效应,从而缓解了梯度消失的问题。
从学习恒等关系的角度看:
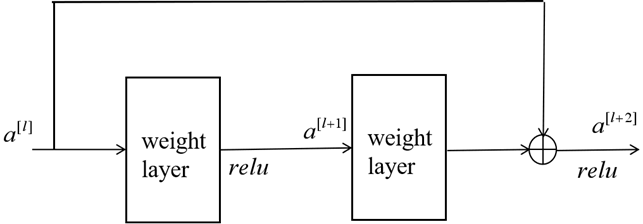
假设第层什么也没学到,
。那么上式就会变为
,即学到的是恒等映射,对整个网络也没有什么影响。
层归一化(Layer Normalization)与批归一化(Batch Normalization):层归一化是在同一样本的不同维度计算均值和方差的。批归一化是不同样本的相同维度计算均值和方差。Transformer采用的是LN。
前馈神经网络(Feed Forward Network, FFN):前馈神经网络通常接在encoder和decoder多头注意力层的后面。由两个线性层和一个非线性激活函数组成。第一个线性层通常将特征映射到高维空间上,后接一个非线性的激活函数进行筛选。第二个线性层通常是变回原来的维度。表达式如下:
参考:
位置编码
https://blog.youkuaiyun.com/xian0710830114/article/details/133377460
Transformer:
19、Transformer模型Encoder原理精讲及其PyTorch逐行实现_哔哩哔哩_bilibili
真-极度易懂Transformer介绍_哔哩哔哩_bilibili
A Survey of Transformers
残差连接:残差神经网络为什么可以缓解梯度消失?_残差结构为啥会解决梯度-优快云博客























 2864
2864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








