机器学习之线性回归的探索

引入

对于房价预测大家应该都已经比较熟悉了，我们给出预测房价的一个重要信息，例如面积多少平方米，可以得出一个大概房价的数据值，这其实就是一个简易版的线性回归模型（术语叫单变量线性回归模型），你将房屋面积输入到这个模型中，他给出你想要的价格，这不就是我们想要达到的目的吗。下面根据这个超级简单的房价预测案例继续往下开辟新的道路。

单变量线性回归

    我们看这张图大致明白右边y是我们的房价（术语叫标签），左边x是我们的面积大小（术语叫特征），（小知识补充：这个图中一行叫做一个样本）大家利用数学逻辑思考会得出一个很简单的一个一次函数： $y=k\ast x+b$

    从图分析我们大致可以得出一个 $y=1/5\ast x+b$ , b代表它们每个值的上下波动，例如第一个就是$460=1/5\ast 2104+39.2$，第二个就是$232=1/5\ast 1416-51.2$，39.2与51.2就分别代表的是它们的波动，但我们的一次函数就一个，为什么只有一个各位明白吧，因为我们肯定只想输入一个面积的值，它能直接输出大概的房价，而不是精准的在所有数据里去找到一个和你输入的数值一模一样的一个样本然后再告诉你这个房价是多少，有和你输入一模一样的倒还好，万一没有呢，那不是直接程序报错，所以我们只要一个函数，你输入面积，它直接告诉你这个房价值多少钱，这才是你想要的，因此我将我们的一次函数改改，改成我们最终想要的模型 : $h=\theta {}_0+\theta {}_1\ast x$（h代表预测值，$\theta {}_0$和$\theta {}_1$是我们要调整的两个参数，这个式子起始就是上面一次函数的变形）

图一

图二

    图一和图二的横纵坐标分别代表房屋面积与房价，我将多个样本的数据可视化得到了这样的两个图，图中的线就是我们的预测线（ $h=\theta {}_0+\theta {}_1\ast x$），图一是随便给的一根线，会发现每个样本几乎都不在这条线上，图二是经过图一无数次的调整（调整$\theta {}_0$和$\theta {}_1$）得出的一根能尽可能穿过所有样本的一根线，这个调整过程的具体细节我们弄明白了，这根线不就出来了，模型的参数也就确定了，那不就可以用这个模型对未知的数据进行房价的预测了。下面将具体解析从图一到图二的具体分析。

代价函数（最小二乘法）的提出
    预测线我们可以随机初始$\theta {}_0$和$\theta {}_1$，那么对应的每一个样本都会有一个对应的预测值，就第一个样本我们可以写成$h{}_1=\theta {}_0+\theta {}_1\ast x{}_1$（下标1代表第一个样本），对应这个样本的真实值我们会产生一个误差error，表示为：$e{}_1=y{}_1-h{}_1$（$y{}_1$真实的房价），这里我们可以看出我们的误差符合均值为0的正态分布，（提问）为什么符合正太分布，因为根据中心极限定理，在大量的样本情况下，如果我们的样本都大致的在我们预测线的周围，那么误差会在一定范围内波动，什么样子的数据符合正太分布，独立同分布，独立这里每一个样本都是互相独立不干扰，同分布就是上面说的它们的误差在一定范围，所以我们判定误差呈现出了正太分布，均值为0是我们的假设。公式写为:$P（e_i）=\frac{1}{\sqrt{2\pi }\sigma }\ast exp(-\frac{e_i^2}{2{\sigma }^2})$，最终变成：$P（y_i|x_i;\theta ）=\frac{1}{\sqrt{2\pi }\sigma }\ast exp(-\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2})$，从这里可以看出只有$\theta$对最后的结果有影响

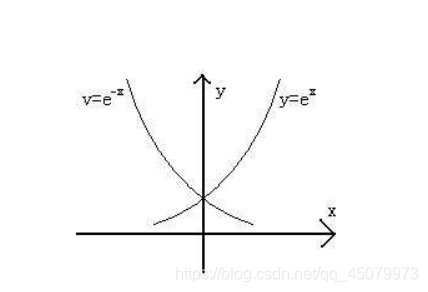
    这里引入极大似然估计函数，该函数的意义，在已知结果的情况下，我们反过来求未知的参数，也就是通过参数$\theta$的确定，让我们的数据尽可能地拟合样本数据，从而最大化的让我们的预测数据趋近真实数据，极端的去想，若我们的每个样本都没有一丝误差，那么误差为0，式子$P（y_i|x_i;\theta ）=\frac{1}{\sqrt{2\pi }\sigma }\ast exp(-\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2})$中的后面式子$\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2}$整体是一个非负的值（不看那个符号），看上图我们可以看出$y=e^{-x}的图像$在x为正的时候只有当x为0时取到最大值，刚好当误差为0时整个式子取到最大值,所有样本误差都为0,那他们整体相乘的那个值也将会是最大的，那我们只需要计算所有样本概率相乘并让整个式子最大得到的参数不就是我们想要的参数吗，这就是极大似然估计的魅力。给出整体累乘的式子，如下：

我们能发现累乘实在是难以计算，所以整体取对数，方便我们计算
$l(\theta )=logL(\theta )=log\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\ast exp(-\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2})$
这里简单讲一个式子$log(a+b)=loga+logb（这里设底为10）$，所以将上式可以转变为:（极大似然估计中的log对数是以e为底的）
$l(\theta )=\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }\ast exp(-\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2})$
展开化简:
$l(\theta )=\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }-\sum _{i=1}^m(\frac{（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2}{2{\sigma }^2})=\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{2}\ast \frac{1}{{\sigma }^2}\sum _{i=1}^m（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2$
从化简好的式子中我们可以看出前面的式子$\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }$如果样本不变的话$\sigma$就不会改变，这不就是一个常数吗，那想要$l(\theta )$最大化不就是想要后面的减式$\frac{1}{2}\ast \frac{1}{{\sigma }^2}\sum _{i=1}^m（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2$最小化吗，这里大家得要明白一件事，这个减式是一个二次函数，那它就会有最低点，它的最低点和前面的常数是没有任何关系的，所以为了方便计算我们保留$\frac{1}{2}$（方便后面求导），后面的$\frac{1}{{\sigma }^2}$舍去就是我们推导出来的最小二乘公式:$\frac{1}{2}\ast \sum _{i=1}^m（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2$
这个求出来的是整体样本的累和，一般我们求出来一个才能看出效果所以求个均值（除以总的样本数m）表示一个样本的损失，最小二乘公式还有一个名字叫代价函数：$J(\theta )=\frac{1}{2m}\ast \sum _{i=1}^m（{\theta }_0+{\theta }_1\ast x_i-y_i{）}^2$

求代价函数的最小值
一.梯度下降法（这里指的是批量梯度下降，想深刻理解所有梯度下降请各位百度一下）
    既然是梯度下降法，首先得知道什么是梯度，梯度指的是某函数在某点的方向导数取得的最大值，叫做梯度。这里我是看的网上的定义跟大家说的，方向导数的最大值其实就是这个函数在这个点对所有参数求偏导后的一个组合方向。
    梯度下降是一个用来求函数最小值的算法，它的背后思想是：开始随机初始化我们的参数，计算代价函数，然后寻找一个能让我们的代价函数值下降最多的参数组合

梯度下降法的直观理解(图有点丑)

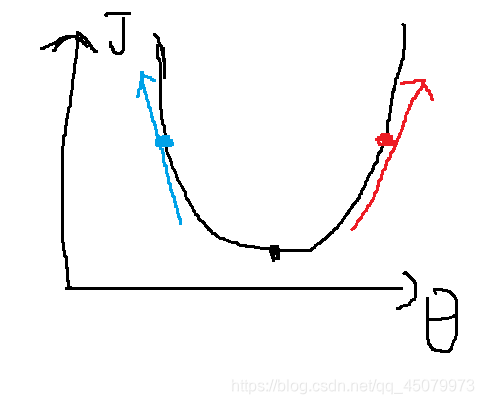
在这个图可以看代价函数是一个凸函数，黑色谷点是最终想要达到的位置，如果说刚开始随机出来的参数在蓝点，它在该点出的导数也就是蓝线，只要将参数往蓝线的反方向就能下降到最低点，如果说刚开始随机出来的参数在红点，它在该点出的导数也就是红线，只要将参数往红线的反方向就能下降到最低点，结论就是无论参数的初始值处于代价函数的哪一边，梯度下降都向最低点移动，也证明明了梯度下降的方向就是该参数导数的反方向。用公式书写为：$\theta :=\theta -\alpha \frac{\delta J(\theta )}{\delta \theta }$ $\alpha$是学习率也可以叫步长，它是一个大于0的一个很小的经验值，它决定让我们代价函数下降的程度有多大，如果$\alpha$太小，梯度下降就会很慢很慢，如果$\alpha$太大，梯度下降可能会没办法收敛，甚至发散出去。再看公式我们最重要的是在于求出代价函数对我们参数的偏导数，下面是我手推过程（有问题及时指出）

二.正规方程法（重点说明正规方程只适用于线性回归）
首先我们要明确的知道我们的代价函数在最低点的时候的任意参数偏导数都是0，这里也是手推过程

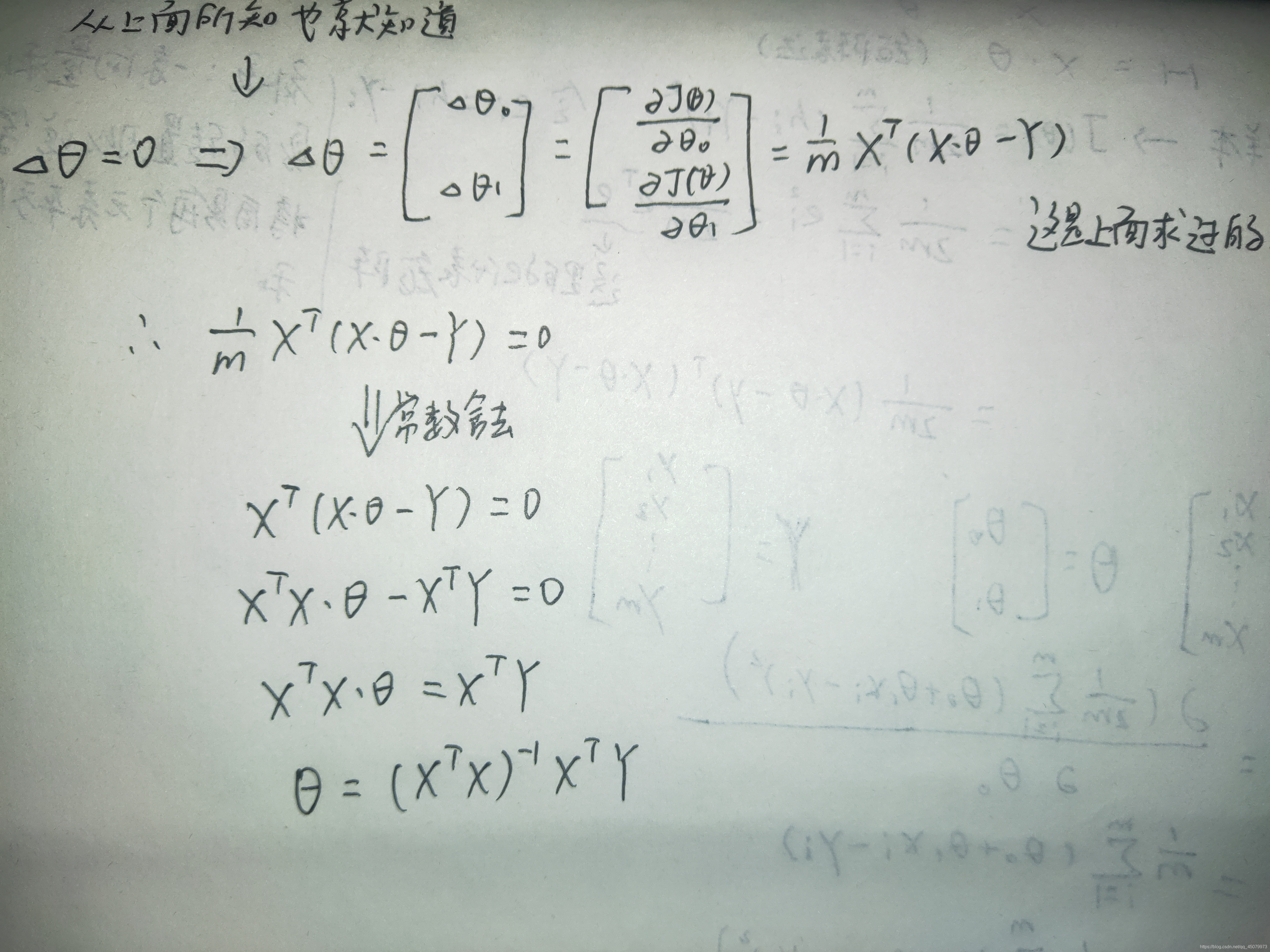
根据这个我们可以一眼看出用正规方程法求解的一个缺点，它要求我们的$X^{T}X$要有逆矩阵，不然无法求解。

总结

    经过上面的操作我们可以得到最终的模型，这个模型可以帮助你预测某面积大小的房价，今天单变量线性回归大致就结束了，喜欢我讲解的小伙伴可以关注一下，第一篇博客可能很垃圾，希望各位多多包涵
    在这里讲一下我对线性回归的定义：寻找一个模型，最大程度的拟合我们的初始数据，也就是训练数据，这个模型一般是一个一次函数，之后再利用这个模型对与训练数据具有相同属性（譬如本博客都是面积，不可能你训练的时候是面积，用房间数输入到模型中预测吧）的未知数据进行预测，输出一个连续的预测值