独轮车问题

问题：

独轮车的轮子上有5种颜色，每走一格颜色变化一次，独轮车只能往前推，也可以在原地旋转，每走一格，需要一个单位的时间，每转90度需要一个单位的时间，转180度需要两个单位的时间。现给定一个20×20的迷宫、一个起点、一个终点和到达终点的颜色，问独轮车最少需要多少时间到达。

分析

1. 此题为一个迷宫问题，需要使用搜索算法确定遍历路径。
2. 独轮车当前的颜色有5种可能，当前独轮车的面朝方向有4种可能，即每个可以到达 的点上有 4X5=20 种状态。
3. 简化问题，独轮车只有三个动作可以选择，独轮车只能前进或左右旋转，并且每做一个动作，需花费一个单位时间。
4. 求最短时间，因此考虑使用BFS算法。在进行广度优先遍历的时候，所遍历的层次就是所花费的时间。

解决思路

一.先解决迷宫从起点找终点的问题

1.使用BFS搜索算法，需使用队列的数据结构

如图所示，从起点S,到终点T,在起点S处，此时状态1独轮车有三个动作可做选择，即前进2，左转3，右转4。所以遍历完1状态后，1状态出队，2、3、4状态进队。

2.完成三种不同动作，当前的独轮车面朝方向的变化

可将如图所示的四个方向，从N开始顺时针依次存入数组中

以下是完成三种动作后，独轮车当前面朝方向的变化。（比如，当独轮车面朝N，向左转后面朝W,向右转后面朝E）

1.直走：当前方向保持不变
2.左转：方向数组向右循环数三个(i + 3)%4
3.右转：方向数组向右循环数一个(i + 1)%4

3.完成三种不同动作，独轮车位置坐标的变化

如图所示，建立以下坐标：

当左右旋转时，独轮车的位置保持不变，当前进时，位置坐标变化如下：
（当独轮车面朝N前进时，Y坐标保持不变，X坐标减1）

二.解决加上轮子颜色的条件

假设五种颜色分别为：
红、黄、蓝、白、绿（依顺时针序）5种颜色，如图所示存入数组

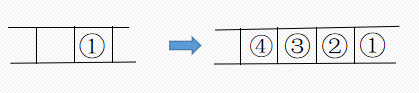
用color数组，每走一格颜色变化一次，当左右旋转时，轮子颜色不发生变化，当前进时，当前的颜色变为(i + 1)%5。

三.完整代码

#include <stdio.h>
#include <queue>
using namespace std;

queue<struct node> qu;
char color[5] = {'R', 'Y', 'B', 'W', 'G'};//颜色数组
int d[4] = {'N', 'E', 'S', 'W'}; //方向数组
int x[4] = {-1, 0, 1, 0};
int y[4] = {0, 1, 0, -1};

int mark[21][21][4][5]; //表示每个格子上的不同的状态  位置 - 方向 - 颜色
char maze[21][21];//地图

struct node{
	int x;
	int y;
	int n_color;
	int d;
	int c;//层次变量
};

void bfs(int sx, int sy, int ex, int ey, int d, int s_color, char e_color){
	int i, j;
	struct node start,temp,tmp;
	int c = 0;//广搜层次变量
	start.x = sx;
	start.y = sy;
	start.n_color = s_color;
	start.d = d;
	start.c = c;
	qu.push(start);
	mark[sx][sy][d][s_color] = 1;//标记该点的该状态
	while(!qu.empty()){
		temp = qu.front();
		qu.pop();

		if(temp.x == ex && temp.y == ey && color[temp.n_color] == e_color){
			printf("%d\n",temp.c);
			return;
		}
		else{
			if(maze[temp.x + x[temp.d]][temp.y + y[temp.d]] == '.' && mark[temp.x + x[temp.d]][temp.y + y[temp.d]][temp.d][(temp.n_color + 1)%5] == 0){//直走
				mark[temp.x + x[temp.d]][temp.y + y[temp.d]][temp.d][(temp.n_color + 1)%5] = 1;
			 	tmp.x = temp.x + x[temp.d];  //位置，方向，颜色 ，层次
			 	tmp.y = temp.y + y[temp.d];
				tmp.d = temp.d;
				tmp.n_color = (temp.n_color + 1)%5;
				tmp.c = temp.c + 1;
				qu.push(tmp);
			}
			if(mark[temp.x][temp.y][(temp.d + 3)%4][temp.n_color] == 0){//左转
				mark[temp.x][temp.y][(temp.d + 3)%4][temp.n_color] = 1;
				tmp.x = temp.x;  //位置，方向，颜色 ，层次
			 	tmp.y = temp.y;
				tmp.d = (temp.d + 3)%4;
				tmp.n_color = temp.n_color;
				tmp.c = temp.c + 1;
				qu.push(tmp);
			}
			if(mark[temp.x][temp.y][(temp.d + 1)%4][temp.n_color] == 0){//右转
				mark[temp.x][temp.y][(temp.d + 1)%4][temp.n_color] = 1;
				tmp.x = temp.x;  //位置，方向，颜色 ，层次
			 	tmp.y = temp.y;
				tmp.d = (temp.d + 1)%4;
				tmp.n_color = temp.n_color;
				tmp.c = temp.c + 1;
				qu.push(tmp);
			}
		}
	}
}

int main()
{
	int sx, sy, ex, ey;
	char c1, ds, c2;
	int i, j;
	int n_d;//方向数组的下标
	int n_color;//颜色数组的下标
	scanf("%d %d %c %c",&sx, &sy, &c1, &ds);
	scanf("%d %d %c",&ex, &ey, &c2);

	getchar();//处理上一个输入的换行
	for(i=1; i<21; i++){
		for(j=1; j<21; j++){
			scanf("%c",&maze[i][j]);
		}
		getchar();
	}


	for(i=0; i<5; i++){//确定颜色数组的初始下标
		if(color[i] == c1){
			n_color = i;
			break;
		}
	}

	for(i=0; i<4; i++){//确定方向数组的初始下标
		if(d[i] == ds){
			n_d = i;
			break;
		}
	}

	bfs(sx, sy, ex, ey, n_d, n_color, c2);
}

四.测试用例

1 6 R N
15 17 E
XXXXXXXXXXXXXXXXXXXX
X.X…XXXXXX…XX
X.X.X…X…XXXX…X
X.XXXXXXX.XXXXXXXX.X
X.X.XX…X…X
X…XXXXX.X.XX.X.XXX
X.X.XX…X.X…X.X.X
X.X.X…XX…XXXX.XXX
X.X.XX.XX.X…X.X.X
X.X…XX.X.XX.X.X.X
X.X.X.XXXXX.XX.X.XXX
X.X.X.XXXXX…X…X
X.X…X.XX…X.X
X.XXX.XXX.X.XXXXXXXX
X…XX…X…X
XXXXX…X.XXXXXXX.X
X…XXXXXXX.XXX.XXX.X
X.XX…X…X
X…X.XXXX.XXXX…XXX
XXXXXXXXXXXXXXXXXXXX