杨辉三角（个人觉得值得总结的东西）

最新推荐文章于 2024-11-14 00:45:41 发布

原创最新推荐文章于 2024-11-14 00:45:41 发布 · 3.6k 阅读

4 ·

CC 4.0 BY-SA版权

c 专栏收录该内容

9 篇文章

订阅专栏

杨辉三角，又称帕斯卡三角，是二项式系数的几何排列，揭示了组合数的代数性质。其特点包括：每行两端数为1，每个数等于其上方两数之和，行数与项数的关系，以及与斐波那契数的联系。代码实现部分可供参考，欢迎指正。

杨辉三角

杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。
具体内容：它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。
举例：

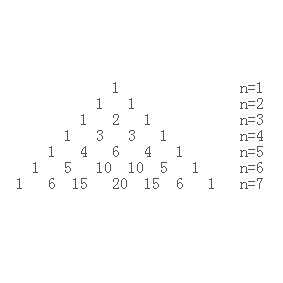
== 前提：每行端点与结尾的数为1==.
（与上图中的n不同，这里第一行定义为n=1）

详细解释：（借鉴百度文库）
每个数等于它上方两数之和。
每行数字左右对称，由1开始逐渐变大。
第n行的数字有n项。
前n行共[(1+n)n]/2 个数。
第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
第n行的第m个数和第n-m+1个数相等，为组合数性质之一。
每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
(a+b)ⁿ的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
具体代码如下：（可能有错误，欢迎大家留言，我可以加以改正）

#include <stdio.h>
void PascalTriangle()
{
    int a[100][100],i,j,num;
    for(i=0;i<100;i++)                                
    {
        for(j=0;j<100;j++)
            {
    a[i][j]=0;
      }
    }
    for(i=0;i<num;i++)                              
       { 
     a[i][0]=1;
 }
    for(i=1;i<num;i++)                               
        {
   for(j=1;j<=i;j++)
            {
    a[i][j]=a[i-1][j]+a[i-1][j-1];
   }
 }
    for(i=0;i<num;i++)                      
    {
        for(j=0;j<=i;j++)
            {
    printf("%d ",a[i][j]);
        printf("\n");
  }
    }
}

主函数：

int main()
{
 PascalTriangle();/*调用函数*/
 return 0;
}