【数据结构笔记】第六章 图 6.2 图的基本概念

6.2 图的基本概念

路径：连续的边构成的顶点序列
路径长度：路径上边或弧的数目/权值之和
回路（环）：第一个顶点和最后一个点顶点相同的路径
简单路径（简单环）：除路径起点和终点相同外，其余顶点均不相同的路径

（a）简单路径

（b）非简单路径

（c）回路

连通图（强连通图）：在无（有）向图G=(V,{E})中，若对任何两个顶点v,u都存在从v到u的路径，称G是连通图（强连通图）

（a）连通图

（b）非连通图

（c）强连通图

（d）非强连通图

权与网：图中边或弧所具有的相关数称为权，表名从一个顶点到另一个顶点的距离或耗损，带权的图称为网
子图：设有两个图G=(V,{E})，G1=(V1,{E1}) 若V1∈V，E1∈E 则称G1是G的子图
连通分量（强连通分量）：
无向图G的极大连通子图称为G的连通分量
极大连通子图：该子图是G连通子图，将G的任何不在该子图中的顶点加入子图不再连通

例,在非连通图中:

有连通分量：

和

这两个都是极大连通分量

有向图G的极大强连通图称为G的强连通分量
极大强连通子图:该子图是强连通子图，将任何不在该子图中的顶点加入子图不再是强连通的

例，在非强连通图中：

有强连通子图

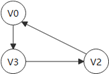
和

且两个均为极大强连通

极小连通子图：该子图是G的连通子图，在该子图中删除任何一条边，子图不在连续
生成树：包含无向图G所有顶点的极小连通子图

例，连通图G1：

G1的生成树：

生产森林：对非连通图，由各个连通分量的生成树的集合