面经整理计划——第一弹

算法&&八股文&&其他

---

一、算法篇

1. 给定一个非负整数num，反复将各个位上的数字相加，直到结果为一位数
   输入：38，输出：2，解释：先3+8=11，再1+1=2，这时候是一位数了所以直接输出，时间复杂度O(1)

分析：简单题(lc258)
假设一个三位数整数n=100a+10b+c,变化后addn=a+b+c；
两者的差值n-addn=99a+9b，差值可以被9整除，说明每次缩小9的倍数
那么我们可以对res=num%9，若不为0则返回res，为0则返回9

class Solution:
    def addDigits(self, num: int) -> int:
        if num==0:
            return 0
        if num%9==0:
            return 9
        return num%9

2. 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
   返回容器可以储存的最大水量。

分析：middle(lc11)
初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。O(n)

class Solution:
    def maxArea(self, height: List[int]) -> int:
        i, j, res = 0, len(height) - 1, 0
        while i < j:
            if height[i] < height[j]:
                res = max(res, height[i] * (j - i))
                i += 1
            else:
                res = max(res, height[j] * (j - i))
                j -= 1
        return res

3. 一座大楼有 n+1 层，地面算作第0层，最高的一层为第 n 层。已知棋子从第0层掉落肯定不会摔碎，从第 i 层掉落可能会摔碎，也可能不会摔碎。
   给定整数 n 作为楼层数，再给定整数 k 作为棋子数，返回如果想找到棋子不会摔碎的最高层数，即使在最差的情况下扔的最小次数。一次只能扔一个棋子。

分析：middle(lc1884)
dp[i][j]为i个棋子扔j次能够辨别的最大n值
动态方程dp[i][j] = dp[i-1][j-1]+1 + dp[i][j-1]
记dp[i-1][j-1]为k,第1颗棋子在k+1层扔下,若碎,剩下i-1颗棋子扔j-1次可得结果;否则剩下i颗棋子扔j-1次。O(knlogn)

import math
class Solution:
    def solve(self , n: int, k: int) -> int:
        b = math.log2(n) + 1 
        #采取二分策略时最差情况所需次数，改善时间复杂度
        if k >= b:
            return int(b)
        dp = [0] * k
        res = 0
        while True:
            tmp = 0
            res += 1
            for i in range(k):
                dp[i], tmp = tmp + dp[i] + 1, dp[i]
                if dp[i] >= n: return res

4. 给定一个长度为n的数组arr，返回arr的最长无重复元素子数组

#双指针
class Solution:
    def maxLength(self , arr ):
        if len(arr) == 0:
            return 0
        d = {}
        startpos = 0
        endpos = 0
        ans = []
        while endpos <= len(arr) - 1:
            if arr[endpos] in d:
                startpos = max(startpos,d[arr[endpos]]+1)      #若出现与d中重复元素,判断重复元素位置与startpos的大小，在startpos前则不管，否则更新startpos
            if endpos - startpos + 1 > len(ans): ans = arr[startpos:endpos+1]               #更新当前最大长度
            d[arr[endpos]] = endpos            #记录扫描过的元素，值-索引
            endpos += 1
        return ans
#队列
class betterSolution:
    def maxLength(self , arr: List[int]) -> int:
        queue = []
        ans = []
        for num in arr:
            while num in queue: queue.pop(0)
            queue.append(num)
            if len(queue) > len(ans): ans = queue
        return ans

5. 给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。
   路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）

分析：middle(lc437)
我们定义节点的前缀和为：由根结点到当前结点的路径上所有节点的和。我们利用先序遍历二叉树，记录下根节点 root 到当前节点 p 的路径上除当前节点以外所有节点的前缀和，在已保存的路径前缀和中查找是否存在前缀和刚好等于当前节点到根节点的前缀和 curr 减去 targetSum

class Solution:
    def pathSum(self, root: TreeNode, targetSum: int) -> int:
        prefix = collections.defaultdict(int)
        prefix[0] = 1

        def dfs(root, curr):
            if not root:
                return 0
            
            ret = 0
            curr += root.val
            ret += prefix[curr - targetSum]
            prefix[curr] += 1
            ret += dfs(root.left, curr)
            ret += dfs(root.right, curr)
            prefix[curr] -= 1

            return ret

        return dfs(root, 0)

二、八股文

1. LSTM和Transformer的原理 (lstm,  transformer)
2. resnet的思想 (resnet)
3. 激活函数的作用 (激活函数)
4. 神经网络都有哪些正则化操作 (regularization)
5. 深度学习中的归一化 (1,  2)
6. Attention和全连接的区别 (区别)
7. 集成学习BAGGING和BOOSTING (1, 2)
8. RF、XGBOOST、LIGHTGBM的特点和区别 (1, 2)

三、其他

1. 系统给定一个可以等概率产生0-10的随机数函数rand11()，老师希望同学们能用这个函数来实现一个可以等概率产生0-6的随机数函数rand7()，有位同学写了如下一段代码，证明该方法的可行性

int rand7(void){
    num = rand11();
    if (num < 7)
        return num;
    return rand7();
}

  Solution
  key point：拒绝采样
  
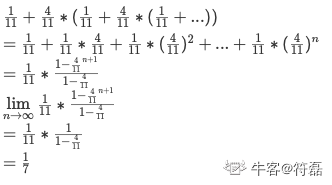
更多参考:
rand5()产生rand7().
算法：根据Rand5()函数构造生成Rand7().

2. Linux基本命令 (1,  2)

---

待解决 (欢迎评论区或私信解答）

1. 给出一个有序数组A和一个常数C，求所有长度为C的子序列中的最大的间距D。
   一个数组的间距的定义：所有相邻两个元素中，后一个元素减去前一个元素的差值的最小值. 比如[1,4,6,9]的间距是2.
   例子：A:[1,3,6,10], C:3。最大间距D应该是4，对应的一个子序列可以是[1,6,10]。

---