
@R星校长
机器学习05【机器学习】
主要内容
- 模型评估方式
- 理解协同过滤思想
- 理解推荐系统架构
- 理解推荐系统流程
学习目标
第一节 模型评估
1. 混淆矩阵:
对以上混淆矩阵的解释:
P:样本数据中的正例数。
N:样本数据中的负例数。
Y:通过模型预测出来的正例数。
N:通过模型预测出来的负例数。
True Positives:真阳性,表示实际是正样本预测成正样本的样本数。
Falese Positives:假阳性,表示实际是负样本预测成正样本的样本数。
False Negatives:假阴性,表示实际是正样本预测成负样本的样本数。
True Negatives:真阴性,表示实际是负样本预测成负样本的样本数。

2. ROC和AUC:
ROC(Receiver Operating Characteristic)曲线和AUC(Area Under the Curve)值常被用来评价一个二值分类器(binary classifier) 的优劣。
ROC曲线是以假阳性率FPR为横轴,以真阳性率TPR为纵轴的一个曲线图像。图像中的每一点是一个分类阈值,根据一些连续的分类阈值可以得到ROC的图像,如下图:有20个样本,其中真实正例有10个,用p表示,负例有10个,用n表示。Inst# 代表样本编号,Class代表样本真实的类别,Score表示利用模型得出每个测试样本属于真实样本的概率。依次将Score概率从大到小排序,得到下表:
从第一个样本开始直到第20个样本,依次将Score当做分类阈值threshold。当预测测试样本属于正样本的概率大于或等于该threshold时,我们认为该样本是正样本,否则是负样本。
如:拿到第一个样本,该样本真实类别是p,Score=0.9,将0.9看成分类阈值threshold,那么该样本预测是正例,TPR=1/10,FPR=0/10=0,拿到第二个样本,该样本真实类别是p,Score=0.8,将0.8作为threshold,该样本预测是正例,TPR=2/10,FPR=0/10=0 … … 以此类推,当拿到第7个样本时,该样本真实类别是n,Score=0.53,将0.53看成分类阈值threshold,预测为正例,但是预测错误,将本该属于负例的样本预测为正例,那么当阈值为0.53时,共预测7个样本,预测正确的样本标号为1,2,4,5,6。预测错误的样本标号为:3,7。那么此时,TPR=5/10=0.5,FPR=2/10=0.2。
按照以上方式,每选择一个阈值threshold时,都能得出一组TPR和FPR,即ROC图像上的一点。通过以上,可以得到20组TPF和FPR,可以得到ROC图像如下,当threshold取值越多,ROC曲线越平滑。
上图图像当样本真实类别为正例时,模型预测该样本为正例那么图像向上画一步(TPR方向)。如果该样本真实类别是负例,模型预测该样本为正例那么图像向右画一步(FPR方向)。
下图中,如果ROC的图像是通过(0,0)点和(1.1)点的一条直线也就是①线,那么当前模型的预测能力是0.5,即:模型在预测样本时,预测对一次,预测错一次,会形成①曲线。如果ROC曲线是②线,那么该模型预测数据的真阳性率大于假阳性率,也就是模型预测对的次数多,预测错的次数少,模型越好。当模型的ROC曲线为③线时,模型的假阳性率比真阳性率大,模型预测错的次数多,预测对的次数少,还不如随机瞎蒙的概率0.5。综上所述,ROC的曲线越是靠近纵轴,越陡,该模型越好。那么如何根据ROC来量化评价一个模型的好坏,这就要用到AUC面积。
AUC面积是ROC曲线与横轴(假阳性率,FPR)围成的面积,也就是曲线下方的面积。AUC面积越大越好,代表模型分类效果更准确。
计算AUC的公式:
其中, 是属于正例的样本。M:测试样本中的正例数。N:测试样本中的负例数。 代表将测试样本(正例和负例都有)中的Score值按照正序排序,找到样本属于正例的索引号累加和。
AUC=1,完美的分类器,采用这个预测模型时,不管设定什么样的阈值都能正确的预测结果。绝大多数情况下,不存在这种分类器。
0.5<AUC<1,优于随机猜测,可以调节分类阈值,使AUC越靠近1,模型效果越好。
AUC=0.5,和随机分类一样,就是随机瞎蒙,模型没有预测价值。
AUC<0.5,比随机分类还差,大多数情况下成功避开了正确的结果。

第二节 决策树和随机森林
决策树和随机森林都是非线性有监督的分类模型。
决策树是一种树形结构,树内部每个节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶子节点代表一个分类类别。通过训练数据构建决策树,可以对未知数据进行分类,
随机森林是由多个决策树组成,随机森林中每一棵决策树之间没有关联,在得到一个随机森林后,当有新的样本进入的时候,随机森林中的每一棵决策树分别进行判断,分析出该样本属于哪一类,然后最后看哪一类被选择最多,就预测该样本属于这一类。
1. 认识决策树
术语:
根节点:最顶层的分类条件
叶节点:代表每一个类别号
中间节点:中间分类条件
分支:代表每一个条件的输出
二叉树:每一个节点上有两个分支
多叉树:每一个节点上至少有两个分支

2. 决策树分类原则
如下图数据集:
要按照前 4 列的信息,使用决策树预测车祸的发生,如何选择根节点呢?
按照 “天气” 列作为根节点,使用决策树预测,如图:
按照 “温度” 列作为根节点,使用决策树预测,如图:
按照 “湿度” 列作为根节点,使用决策树预测,如图:
使用 “风” 列作为根节点,使用决策树预测,如图:
通过以上发现,只有使用天气作为根节点时,决策树的高度相对低而且树的两边能将数据分类的更彻底(其他列作为根节点时,树两边分类不纯粹,都有天气)。
决策树的生成原则:数据不断分裂的递归过程,每一次分裂,尽可能让类别一样的数据在树的一边,当树的叶子节点的数据都是一类的时候,则停止分类。这样分类的数据,每个节点两边的数据不同,将相同的数据分类到树的一侧,能将数据分类的更纯粹。减少树的高度和训练决策树的迭代次数。注意:训练决策树的数据集要离散化,不然有可能造成训练出来的树有些节点的分支特别多,容易造成过拟合。
3. 选择分类条件
下图:
上图中箱子①中有100个红球。箱子②中有50个红球和50个黑球。箱子③中有10个红球和30个篮球,60个绿球。箱子④中各个颜色均有10中球。发现箱子①中球类单一,信息量少,比较纯粹,箱子④中,球的类别最多,相对①来说比较混乱,信息量大。
如何量化以上每个箱子中信息的纯粹和混乱(信息量的大小)指标,可以使用信息熵或者基尼系数。
1). 信息熵:信息熵是香农在1948年提出来量化信息信息量的指标,熵的定义如下:

计算 “是否购买电脑” 这列的信息熵,当前类别 “是否购买电脑” 有 2 个类别,分别是 “是” 和 “否”,那么 “是否购买电脑” 类别的信息熵如下:
通过以上计算可以得到,某个类别下信息量越多,熵越大,信息量越少,熵越小。假设“是否购买电脑”这列下只有“否”这个信息类别,那么“是否购买电脑”这列的信息熵为:
上图中,如果按照“年龄”,“收入层次”,“学生”,“信用等级”列使用决策树来预测“是否购买电脑”。如何选择决策树的根节点分类条件,就是找到某列作为分类条件时,使“是否购买电脑”这列分类的更彻底,也就是找到在某个列作为分类条件下时,“是否购买电脑”信息熵相对于没有这个分类条件时信息熵降低最大(降低最大,就是熵越低,分类越彻底),这个条件就是分类节点的分类条件。这里要使用到条件熵和信息增益。
H(是否购买电脑|年龄)=H(是否购买电脑|青少年)+H(是否购买电脑|中年)+H(是否购买电脑|老年)
在“年龄”条件下,“是否购买电脑”的信息增益为:
g(是否购买电脑,年龄)=H(是否购买电脑)-H(是否购买电脑,年龄)
=0.94-0.69=0.25
由以上可知,按照“记录ID”,“年龄”,“收入层次”,“学生”,“信用等级”列使用决策树来预测“是否购买电脑”,选择分类根分类条件时步骤:
a.计算 “是否购买电脑” 的信息熵
b.计算在已知各个列的条件熵
H(是够购买电脑|年龄),H(是够购买电脑|收入层次),H(是够购买电脑|是否学生),H(是够购买电脑|信用等级)
c.求各个条件下的信息增益,选择信息增益大的作为分类条件。选择中间节点时,以此类推。
在构建决策树时,选择信息增益大的属性作为分类节点的方法也叫ID3分类算法。
2).基尼系数:基尼系数也可以表示样本的混乱程度。公式如下: 基尼系数越小代表信息越纯,类别越少,基尼系数越大,代表信息越混乱,类别越多。基尼增益的计算和信息增益相同。假设某列只有一类值,这列的基尼系数为0。
基尼系数越小代表信息越纯,类别越少,基尼系数越大,代表信息越混乱,类别越多。基尼增益的计算和信息增益相同。假设某列只有一类值,这列的基尼系数为0。
4. 信息增益率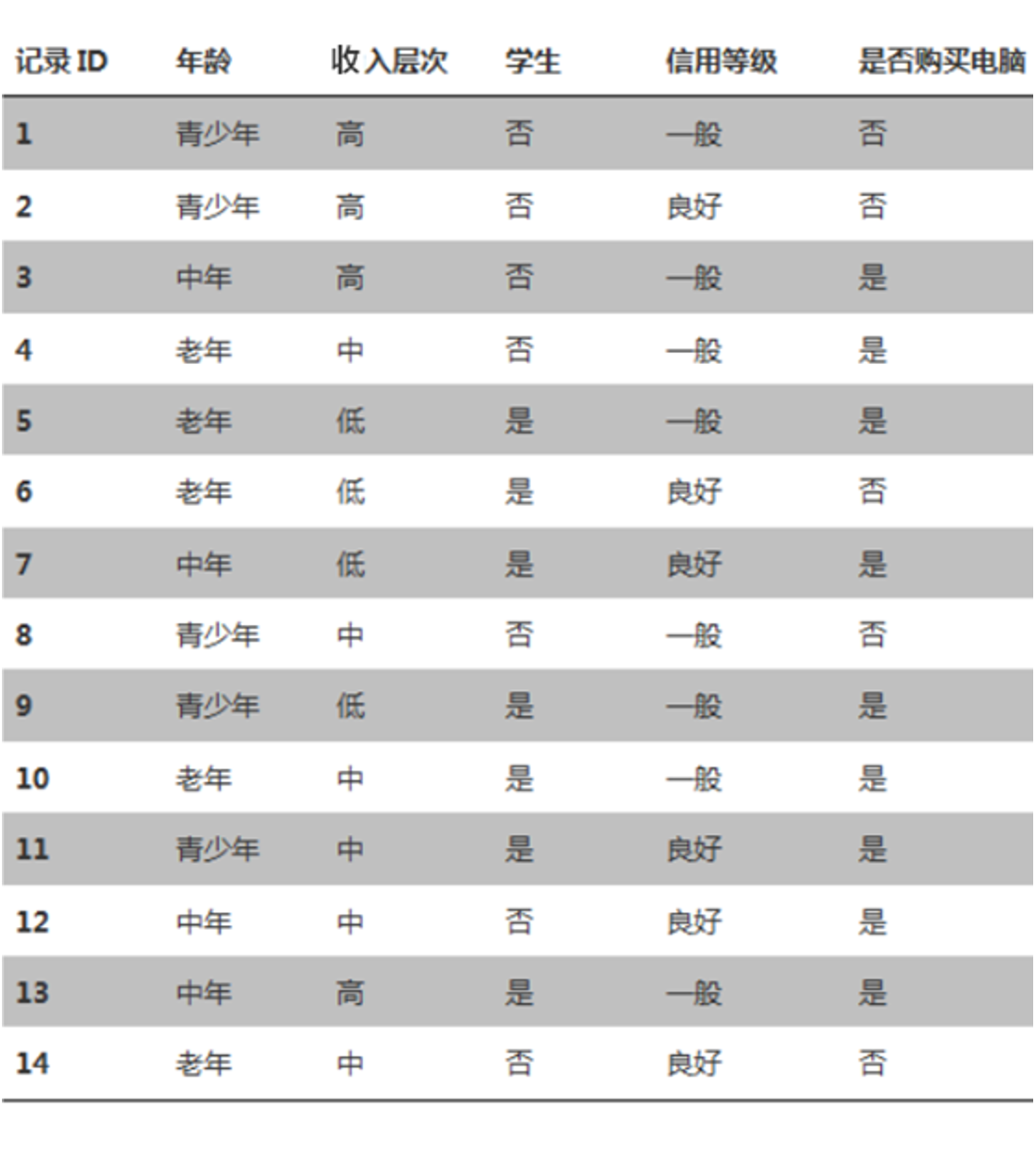
在上图中,如果将“记录ID”也作为分类条件的话,由于“记录ID”对于“是否购买电脑”列的条件熵为0,可以得到“是否购买电脑”在“记录ID”这个分类条件下信息增益最大。如果选择“记录ID”作为分类条件,容易造成分支特别多,对已有记录ID的数据可以分类出结果,对于新的记录ID有可能不能成功的分类出结果。
使用信息增益来筛选分类条件,更倾向于选择更混杂的属性。容易出现过拟合问题。可以使用信息增益率来解决这个问题。
信息增益率的公式:gr(D,A) = g(D,A)/H(A),在某个条件下信息增益除以这个条件的信息熵。
例如:在“记录ID”条件下,“是否购买电脑”的信息增益最大,信息熵H(记录ID)也比较大,两者相除就是在“记录ID”条件下的信息增益率,结果比较小,消除了当某些属性比较混杂时,使用信息增益来选择分类条件的弊端。使用信息增益率来构建决策树的算法也叫 C4.5 算法。一般相对于信息增益来说,选择信息增益率选择分类条件比较合适。
如果决策树最后一个条件依然没能将数据准确分类,那么在这个节点上就可以使用概率来决定。看看哪些情况出现的多,该情况就是该节点的分类结果。
5. 使用决策树来做回归或者预测值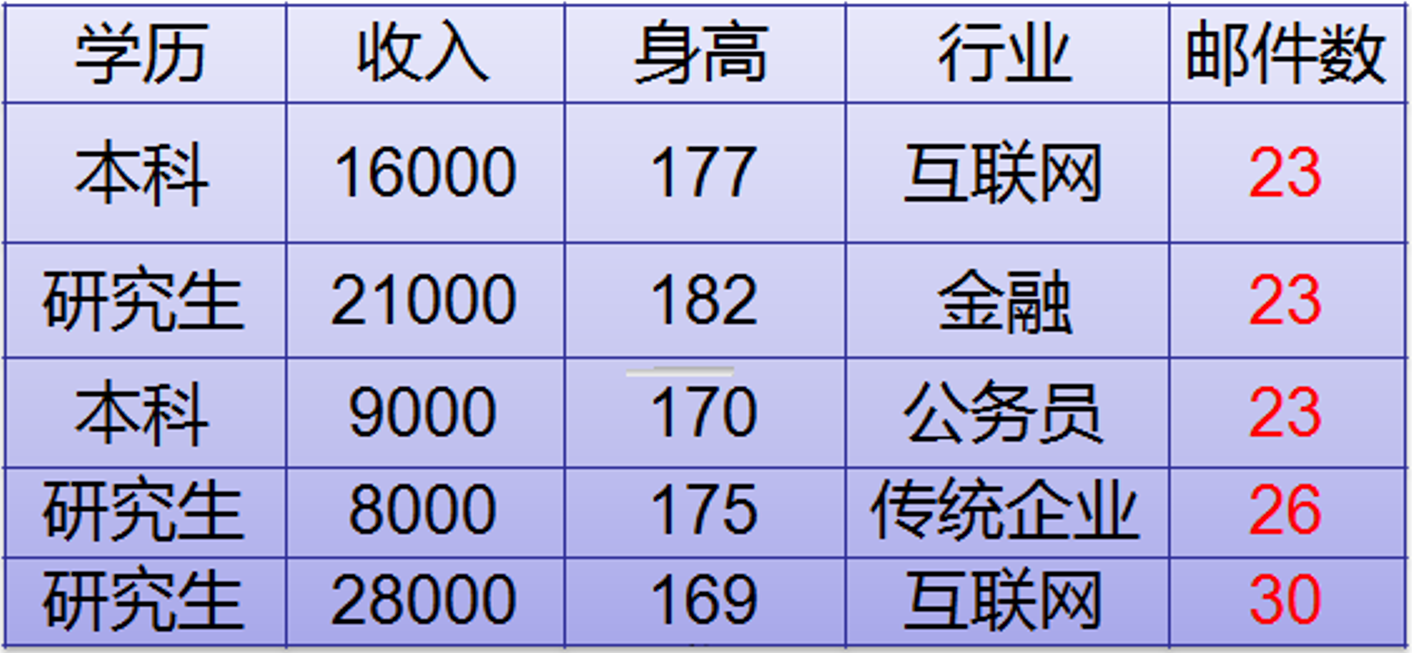
 机器学习模型评估与决策树:ROC、AUC及推荐系统详解
机器学习模型评估与决策树:ROC、AUC及推荐系统详解





 本文介绍了机器学习中的模型评估,重点讲解了ROC曲线和AUC值的概念,以及它们在评估分类器性能中的作用。接着,文章深入探讨了决策树和随机森林,包括它们的工作原理和优缺点。此外,还讨论了协同过滤在推荐系统中的应用,以及App推荐系统的基本架构和推荐流程。
本文介绍了机器学习中的模型评估,重点讲解了ROC曲线和AUC值的概念,以及它们在评估分类器性能中的作用。接着,文章深入探讨了决策树和随机森林,包括它们的工作原理和优缺点。此外,还讨论了协同过滤在推荐系统中的应用,以及App推荐系统的基本架构和推荐流程。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2606
2606

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








