2022/1/22笔记

基本语法

1.sort对vector排序C++ vector用法详解

     分为升序和降序两排序方式：
     vector<int>v;
     sort(v.begin(), v.end(),less<int>());//升序
     sort(v.begin(), v.end(),greater<int>());//降序
     sort(obj.begin(),obj.end());//从小到大
     reverse(obj.begin(),obj.end());反向迭代器,实现元素对调
     obj.clear();//清除容器中所以数据

2.map的遍历输出以及计数

#include <iostream>                     0 : 1
#include <map>
using namespace std;                    1 : 3
int main() {                            10 : 10
    map<int, int> stu_map;              0 : 1
    stu_map[0] = 1;                     1 : 3
    stu_map[1] = 2;                     10 : 10
    stu_map[1]++;                       3
    stu_map[10] = 10;                   0
    map<int, int>::iterator iter;       100
    iter = stu_map.begin();
    while(iter != stu_map.end()) {
        cout << iter->first << " : " << iter->second << endl;
        iter++;
    }
    for(auto iter1 = stu_map.begin(); iter1 != stu_map.end(); iter1++) {
        cout << iter1->first << " : " << iter1->second << endl;
    }
    cout<<stu_map[1]<<endl;        //输出的是3
    cout<<stu_map[5]<<endl;        //对于map中没有的输出的是0
    stu_map[1]=100;                //map[d]可以幅值
    cout<<stu_map[1]<<endl;        //输出是100
    stu_map[6]++;                  //默认是0
    cout<<stu_map[6]<<endl;        //输出是1
    return 0;
}

3.long型和int型的区别

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int a=1,count=0;
        for(int i=0;i<32;i++) {
            if((n&a)!=0) count++;
            a*=2;                  最大的情况是2的31次方所以报错将int改成long a=1;
        }
       return count; 
    }
};
class Solution {      最好改成1<<i 1左移i位
public:
    int hammingWeight(uint32_t n) {
        int ret = 0;
        for (int i = 0; i < 32; i++) 
            if (n & (1 << i))      是2的31次方共有32位
                ret++;
        return ret;
    }
};

 4.负数在计算机的二进制表示

7的二进制形式可以表示如下：   00000000 00000000 00000000 00000111
-7的二进制形式可以表示如下：  11111111 11111111 11111111 11111001
一个正数，按照其本身大小转换成的二进制数，称为原码
一个负数，按照其绝对值大小转换成的二进制数，最高位补1，称为原码
00000000 00000000 00000000 00000111 // 是7的原码
10000000 00000000 00000000 00000111 // 是-7的原码
00000000 00000000 00000000 00000111 // 是7的反码，和原码相同
10000000 00000000 00000000 00000111 // 是-7的原码
11111111 11111111 11111111 11111000 // 对-7的原码取反（除符号位），即得到了-7的反码
00000000 00000000 00000000 00000111 // 是7的补码，和原码相同
11111111 11111111 11111111 11111001 // 最后一位加1，即得到-7的补码，这也是负数在计算机中最终的表示形式 
                                      所以计算机中-A=~A+1

5.位操作位运算操作常见技巧

https://blog.youkuaiyun.com/wat1r/article/details/114298873?spm=1001.2014.3001.5501
# bit操作
& 符号，x & y ，会将两个十进制数在二进制下进行与运算
| 符号，x | y ，会将两个十进制数在二进制下进行或运算
^ 符号，x ^ y ，会将两个十进制数在二进制下进行异或运算
<< 符号，x << y 左移操作，最右边用 0 填充
>> 符号，x >> y 右移操作，最左边用 0 填充
~ 符号，~x ，按位取反操作，将 x 在二进制下的每一位取反

# 整数集合set位运算
# 整数集合做标志时，比如回溯时的visited标志数组
vstd 访问 i ：vstd | (1 << i)
vstd 离开 i ：vstd & ~(1 << i)
vstd 不包含 i : not vstd & (1 << i)

并集 ：A | B
交集 ：A & B
全集 ：(1 << n) - 1
补集 ：((1 << n) - 1) ^ A
子集 ：(A & B) == B
判断是否是 2 的幂 ：A & (A - 1) == 0                     只有一位是1
最低位的 1 变为 0 ：n &= (n - 1)                         最右边的1变成0
最低位的 1：A & (-A)，最低位的 1 一般记为 lowbit(A)        A&(-A)=A&(~A+1)取最右边的1

 题目1原地哈希找到所有数组中消失的数字

原地哈希找到所有数组中消失的数字nums[（数值-1）%8]+8
（数值-1）%len得到下标，再使用下标找到对应的数加上len
通过len做为分界线
[0,1,2,3,4,5,6,7]
[4,3,2,7,8,2,3,1]
[8,8,8,8,0,0,8,8]
[0,8,8,0,0,0,0,0]
时间复杂度：O(n)O(n)。
空间复杂度：O(1)O(1)。返回值不计入空间复杂度
class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        int len=0;
        vector<int>res;             返回值不计入空间复杂度
        len=nums.size();
        for(auto a:nums) {a=(a-1)%len;nums[a]+=len;}
        for(int i=0;i<=len-1;i++){
            if(nums[i]<=len) res.push_back(i+1);
        }
        return res;
    }
};

题目复写

### 解题思路
一般是两个数组双指针遍历
不增加空间，延长从后向前，双指针
### 代码
```cpp
class Solution {
public:
//双指针两个数组
    void duplicateZeros(vector<int>& arr) {
        vector<int> res=arr;
        int p1=0,p2=0;
        while(p2<arr.size()&&p1<arr.size()){  新建一个容器保存原始值，会被覆盖
        if(res[p1]==0&&p2+1<arr.size())
        {
            p1++;
            arr[p2++]=0;
            arr[p2++]=0;
        }
        else if(res[p1]!=0){
            arr[p2++]=res[p1++];
        }
        else {
            arr[p2++]=0;
        }
        }
    }
};
```
```cpp
//双指针单个数组
class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int zero=0;
        int len=arr.size();
        for(int a:arr) if(a==0) zero++;
        int p1=len-1,j=len+zero-1;     j是加上所有0最长的情况，当j大于原来数组长度就直接j--
        while(p1>=0)                   不更新值。从后向前不会被覆盖
        {
            if(arr[p1]==0)
            {
                if(j>=len) j--;
                else arr[j--]=0;
                if(j>=len) j--;
                else arr[j--]=0;
            }
            else 
            {
                if(j>=len) j--;
                else arr[j--]=arr[p1];
            }
            p1--;
        } 
    }
};
```

题目位1数量-位操作 

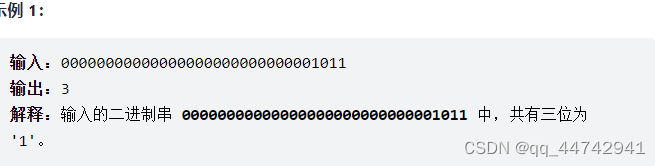
// 位运算n&(n-1)把n最右边的1变成0
// 经过多少次变成0就有几个0
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count=0;
        while(n){
            n&=n-1;
            count++;
        }
       return count; 
    }
};