Poj--1091 跳蚤（容斥定理）

最新推荐文章于 2019-12-21 03:07:19 发布

原创最新推荐文章于 2019-12-21 03:07:19 发布 · 278 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#Poj 1091 #跳蚤

容斥定理专栏收录该内容

1 篇文章

订阅专栏

本文探讨了一种基于跳蚤游戏的数学问题，通过算法分析，解决了跳蚤如何利用特定的数字组合跳跃到指定位置的难题。文章详细介绍了问题背景、解决思路及代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

跳蚤

Z城市居住着很多只跳蚤。在Z城市周六生活频道有一个娱乐节目。一只跳蚤将被请上一个高空钢丝的正中央。钢丝很长，可以看作是无限长。节目主持人会给该跳蚤发一张卡片。卡片上写有N+1个自然数。其中最后一个是M，而前N个数都不超过M，卡片上允许有相同的数字。跳蚤每次可以从卡片上任意选择一个自然数S，然后向左，或向右跳S个单位长度。而他最终的任务是跳到距离他左边一个单位长度的地方，并捡起位于那里的礼物。
比如当N=2，M=18时，持有卡片(10, 15, 18)的跳蚤，就可以完成任务：他可以先向左跳10个单位长度，然后再连向左跳3次，每次15个单位长度，最后再向右连跳3次，每次18个单位长度。而持有卡片(12, 15, 18)的跳蚤，则怎么也不可能跳到距他左边一个单位长度的地方。
当确定N和M后，显然一共有M^N张不同的卡片。现在的问题是，在这所有的卡片中，有多少张可以完成任务。
Input
两个整数N和M(N <= 15 , M <= 100000000)。
Output
可以完成任务的卡片数。
Sample Input

2 4

Sample Output

Hint
这12张卡片分别是： 
(1, 1, 4), (1, 2, 4), (1, 3, 4), (1, 4, 4), (2, 1, 4), (2, 3, 4), 
(3, 1, 4), (3, 2, 4), (3, 3, 4), (3, 4, 4), (4, 1, 4), (4, 3, 4)

题意和解题过程和思路看→这里
在这里插入图片描述
最后一点也可以写成:

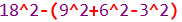
比较好理解

自己看完题解理解以后写的代码：
Code:

#include<cstdio>
#include<iostream>
typedef long long ll;
using namespace std;
const int N=1e5;

int a[N];
ll pow(ll a,ll n)
{
	ll res=1;
	while(n){
		if(n&1)res=res*a;
		n>>=1;
		a*=a;
	}
	return res;
}
int main()
{
	ll n,m,mm;
	scanf("%lld%lld",&n,&m);
	mm=m;
	int k=0;
	for(int i=2;i*i<=m;i++){
		if(m%i==0){
			a[k++]=i;
			while(m%i==0)m/=i;
		}
	}
	if(m>1)a[k++]=m;
	ll ans=pow(mm,n);
	for(int i=1;i<(1<<k);i++){
		ll s=1,kk=0;
		for(int j=0;j<k;j++){
			if(1&(i>>j)){
				s*=a[j];
				kk++;
			}
		}
		s=pow(mm/s,n);
		if(kk&1)ans-=s;
		else ans+=s;
	}
	printf("%lld\n",ans);
	return 0;
 }