二刷GAMES11 Transformation

齐次坐标

引入齐次坐标是想把包含平移在内的变换写成一个矩阵乘以一个向量的形式。

Homogenous Coordinates
2D point \((x,y,1)^T\) 其实是\((x/w,y/w,w)^T\) w不等于0
2D vector \((x,y,0)^T\)

2D Transformations

• 缩放，Scale

\[\mathbf{S}(s_x,s_y)=\begin{pmatrix}s_x&0&0\\0&s_y&0\\0&0&1\end{pmatrix} \]

• 旋转，Rotation

\[\mathbf{R}(\alpha)=\begin{pmatrix}\cos\alpha&-\sin\alpha&0\\\sin\alpha&\cos\alpha&0\\0&0&1\end{pmatrix} \]

• 平移，Translation

\[\mathbf{T}(t_x,t_y)=\begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix} \]

• 斜切，Shear

组合变换

变换顺序很重要，矩阵点乘不符合交换律

仿射变换(Affine transformation)，又称仿射映射，是指在几何中，对一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。
线性变换不改变原点。
齐次坐标通过高纬度的线性变换完成低纬度的仿射变换。
旋转矩阵是正交矩阵，旋转矩阵的逆是旋转矩阵的转置。

3D Transformations

• 缩放，Scale
• 旋转，Rotation
• 平移，Translation

相机成像投影

View/Camera Transformation

定义相机

• Position
• Look-at / gaze direction
• Up direction

一般相机的标准定位

• The origin, up at Y, look at -Z
• And transform the objects along with the camera

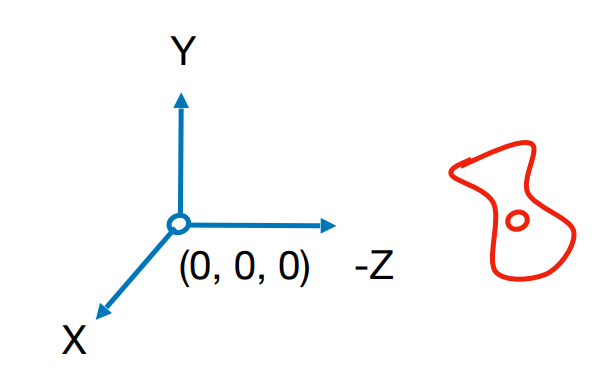
Projection Transformation

将3D转为2D

• 正交投影
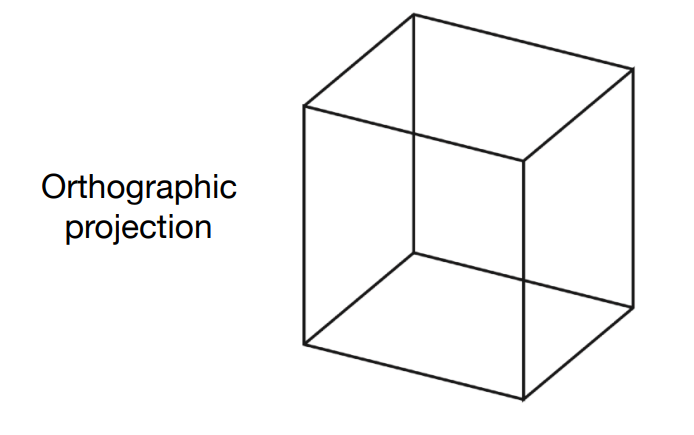
  规范化的过程，平移到原点，缩放到[1,1,1]标准正方体中

• 透视投影
  近大远小
  思路是先将f平面挤压成和n平面一样大小的，然后进行正交投影
  挤压的矩阵定义为\(M_{persp->ortho}\)，同时n平面上的点坐标不变，f平面点z坐标不变。
  推导过程见图。【这个过程其实很奇怪，如果不提前使用齐次坐标的话，这个解不出来，推导过程的重点在于，点的x,y保证相同】
  课上问题：中间的点挤压后z会变大还是变小
  答：z变大了。推导过程如下：

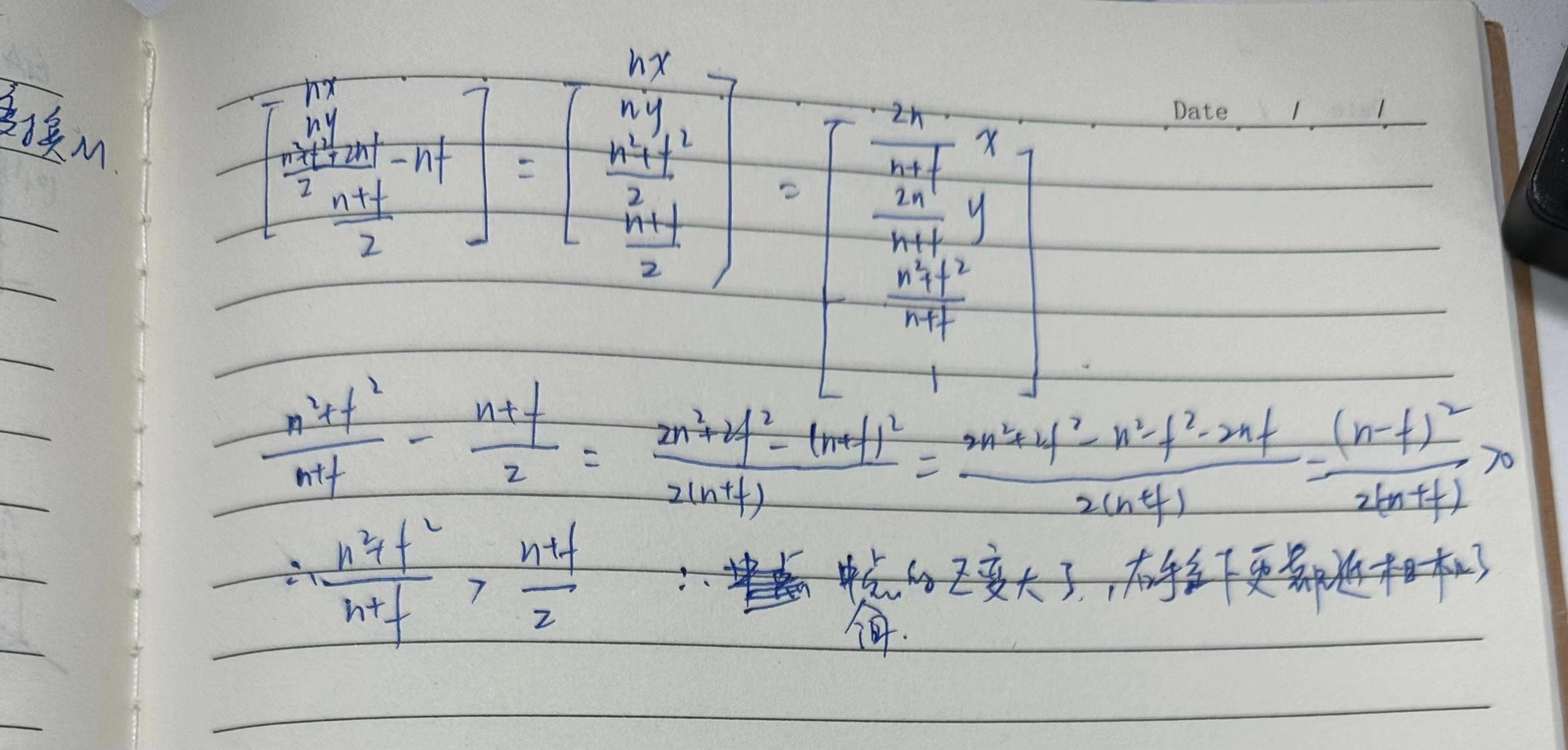
作业

/**
 * @brief 获得模型绕z轴的变换矩阵
 * 
 * @param rotation_angle 绕z轴的旋转角，角度制
 * @return Eigen::Matrix4f 变换矩阵
 */
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // // cos -sin 0 0
    // // sin cos 0 0
    // // 0 0 1 0
    // // 0 0 0 1

    double theta=rotation_angle / 180 * MY_PI; //弧度制

    model<<cos(theta), -sin(theta), 0.0, 0.0,
        sin(theta), cos(theta), 0.0, 0.0,
        0.0, 0.0, 1.0, 0.0,
        0.0, 0.0,0.0, 1.0;

    return model;
}

/**
 * @brief 相机的透视投影矩阵，将透视投影变为正交投影的长方体，再归一化到[1,1,1]的正方体中
 * near 平面点坐标不变
 * far 平面z坐标不变
 * @param eye_fov fov 角度制
 * @param aspect_ratio 宽高比  aspect_ratio=width/hight
 * @param zNear Near平面z坐标
 * @param zFar Far平面z坐标
 * @return Eigen::Matrix4f 
 */
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // 变成长方体 n=zNear f=zFar
    // n 0 0 0
    // 0 n 0 0 
    // 0 0 n+f -fn
    // 0 0 1 0

    Eigen::Matrix4f matrix1 = Eigen::Matrix4f::Identity();
    matrix1<< zNear,0.0 , 0.0 ,0.0 ,
        0.0, zNear, 0.0, 0.0,
        0.0, 0.0, zNear+zFar, -zNear*zFar,
        0.0, 0.0, 1.0, 0.0;
    
    float h=2*tan(eye_fov*MY_PI/(2*180))*zNear;
    float w=aspect_ratio*h;
    // 长方体xyz范围为[-1,1]且原点在[0,0,0]
    Eigen::Matrix4f matrix2 = Eigen::Matrix4f::Identity();
    // 先移动
    matrix2<< 1,0.0 , 0.0 ,0.0 ,
        0.0, 1, 0.0, 0.0,
        0.0, 0.0, 1.0, -(zNear+zFar)/2,
        0.0, 0.0, 1.0, 0.0;
    
    // 再缩放
    Eigen::Matrix4f matrix3 = Eigen::Matrix4f::Identity();
    matrix3<< 2/w,0.0 , 0.0 ,0.0 ,
        0.0, 2/h, 0.0, 0.0,
        0.0, 0.0, 2.0/(zNear-zFar), 0.0,
        0.0, 0.0, 1.0, 0.0;
    projection=matrix3*matrix2*matrix1;

    return projection;
}

其中正交投影的过程要注意z轴的方向，在作业中，为右手系。\((\hat{near}-\hat{far})D\)=\(\hat{1-(-1)}\)=\(\hat2\)
所以，\(D=\frac{2}{(\hat{near}-\hat{far})}\)

效果：