算法基础讲解--LeetCode59.螺旋矩阵

1.力扣原题

题目描述：给你一个正整数n，生成一个包含1到 n^2 所有元素，且元素按顺时针顺序螺旋排列的
n * n 正方形矩阵matrix 。

示例1：
输入：n=3
输出：[ [1,2,3] , [8,9,4] , [7,6,5] ]

2.原理分析

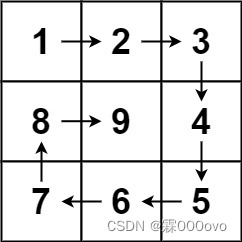
通过题目给的实例图可以看出，这道题主要考察的是代码设计思维，一个正整数3，生成包含1到9的所有元素，按照矩形样式进行数据排列。这道题要注意矩形中四个角的数字，不能重复遍历，从题目示例可以看出，矩形中的遍历是顺时针的，我们根据这个规则，将矩形四个边独立开，一次只遍历一条边，遍历到边角数字之前就停止遍历，开始下一条边的遍历，如下图所示：

用不同的颜色将每一个边所需遍历的范围进行了标注，
1. 红色部分为第一条边(矩形上侧，从左到右遍历)，遍历到边角数字3之前停止遍历；
2. 黄色部分为第二条边(矩形右侧，从上到下遍历)，遍历到边角数字5之前停止遍历；
3. 绿色部分为第三条边(矩形下侧，从右到左遍历)，遍历到边角数字7之前停止遍历；
4. 蓝色部分为第四条边(矩形左侧，从下到上遍历)，遍历到边角数字1之前停止遍历；

这样就形成了一轮的循环遍历，如果第一轮遍历结束没有到n^2，那么进行下一轮遍历，同样也是将四条边分别遍历，但每增加新一轮遍历，则需要注意将边长收缩；另外需要注意的是，如果n为奇数的话，将最后一个数直接填入即可，无需建立新一轮遍历。

3.代码解释

    public int[][] generateMatrix(int n) {
        // loop:循环次数,
        // start:每次循环的开始点(start,start),
        // count:定义填充数字,
        // x:行
        // y:列
        // offset:每一条边遍历的长度，每次循环右边界收缩一位
        int loop = 0, start = 0, count = 1, offset = 1, x, y;
        int[][] res = new int[n][n];

        while (loop < n / 2) {
            //上侧 从左到右遍历
            //res[start][y] = count++ : 填充数字
            for (y = start; y < n - offset; y++) res[start][y] = count++;

            //右侧 从上到下遍历
            for (x = start; x < n - offset; x++) res[x][y] = count++;

            //下侧 从右到左:y已经赋值过了，无需再初始化
            for (; y > start; y--) res[x][y] = count++;

            //左侧 从下到上遍历:x赋值过了，无需再次初始化
            for (; x > start; x--) res[x][y] = count++;

            loop++;
            start++;
            offset++;
        }

        //当n为奇数时
        if (n % 2 == 1) {
            res[start][start] = count;
        }

        return res;
    }