每日刷题(110)
问题 A: 简单计算器
题目描述
读入一个只包含 +, -, *, / 的非负整数计算表达式,计算该表达式的值。
输入
测试输入包含若干测试用例,每个测试用例占一行,每行不超过200个字符,整数和运算符之间用一个空格分隔。没有非法表达式。当一行中只有0时输入结束,相应的结果不要输出。
输出
对每个测试用例输出1行,即该表达式的值,精确到小数点后2位。
样例输入
30 / 90 - 26 + 97 - 5 - 6 - 13 / 88 * 6 + 51 / 29 + 79 * 87 + 57 * 92
0
样例输出
12178.21
C++代码
#include<iostream>
#include<cstdio>
#include<string>
#include<stack>
#include<queue>
#include<map>
using namespace std;
struct node{
double num; //操作数
char op; //操作符
bool flag; //true表示操作数,false表示操作符
};
string str;
stack<node> s;
queue<node> q;
map<char, int> op;
void Change() //中缀转后缀
{
double num;
node temp;
for(int i = 0; i < str.length(); )
{ //如果是数字
if(str[i] >= '0' && str[i] <= '9')
{
temp.flag = true;
temp.num = str[i++] - '0'; //新节点已就绪
//当该操作数为多位数时
while(i < str.length() && str[i] >= '0' && str[i] <= '9')
{
temp.num = temp.num * 10 + (str[i] - '0');
i++;
}
q.push(temp);
}
else
{ //如果是操作符
temp.flag = false;
while(!s.empty() && op[str[i]] <= op[s.top().op])
{
q.push(s.top());
s.pop();
}
temp.op = str[i];
s.push(temp);
i++;
}
}
while(!s.empty()) //把操作符栈中的所有操作符弹出
{ //并压入队列中
q.push(s.top());
s.pop();
}
}
double Cal() //计算后缀表达式
{
double temp1, temp2;
node cur, temp;
while(!q.empty())
{
cur = q.front();
q.pop();
if(cur.flag == true) //是操作数则压入栈中
{
s.push(cur);
}
else
{
temp2 = s.top().num;
s.pop();
temp1 = s.top().num;
s.pop();
temp.flag = true;
if(cur.op == '+')
{
temp.num = temp1 + temp2;
}
else if(cur.op == '-')
{
temp.num = temp1 - temp2;
}
else if(cur.op == '*')
{
temp.num = temp1 * temp2;
}
else if(cur.op == '/')
{
temp.num = temp1 / temp2;
}
s.push(temp);
}
}
return s.top().num;
}
int main()
{
op['+'] = op['-'] = 1;
op['*'] = op['/'] = 2;
while(getline(cin, str), str != "0")
{
for(string::iterator it = str.end(); it != str.begin(); it--)
{
if(*it == ' ')
str.erase(it);
}
while(!s.empty())
{
s.pop();
}
Change();
printf("%.2f\n", Cal());
}
return 0;
}
样例运行结果:

表达式的概念(前中后缀表达式)

逆波兰表达式(后缀表达式)
逆波兰表达式又叫做后缀表达式。逆波兰表示法是波兰逻辑学家J・卢卡西维兹(J・ Lukasiewicz)于1929年首先提出的一种表达式的表示方法 。后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。逆波兰表达式把运算量写在前面,把算符写在后面。
后缀表达式的特点就是:每一运算符都置于其运算对象之后,以上面的中缀表达式1 + 2 * 3为例子,转为后缀表达式就是123 * +


中缀表达式
先说一下中缀表达式,平时我们使用的运算表达式就是中缀表达式,例如1+3*2,中缀表达式的特点就是:二元运算符总是置于与之相关的两个运算对象之间

人读起来比较好理解,但是计算机处理起来就很麻烦

中缀VS后缀


算法演示一


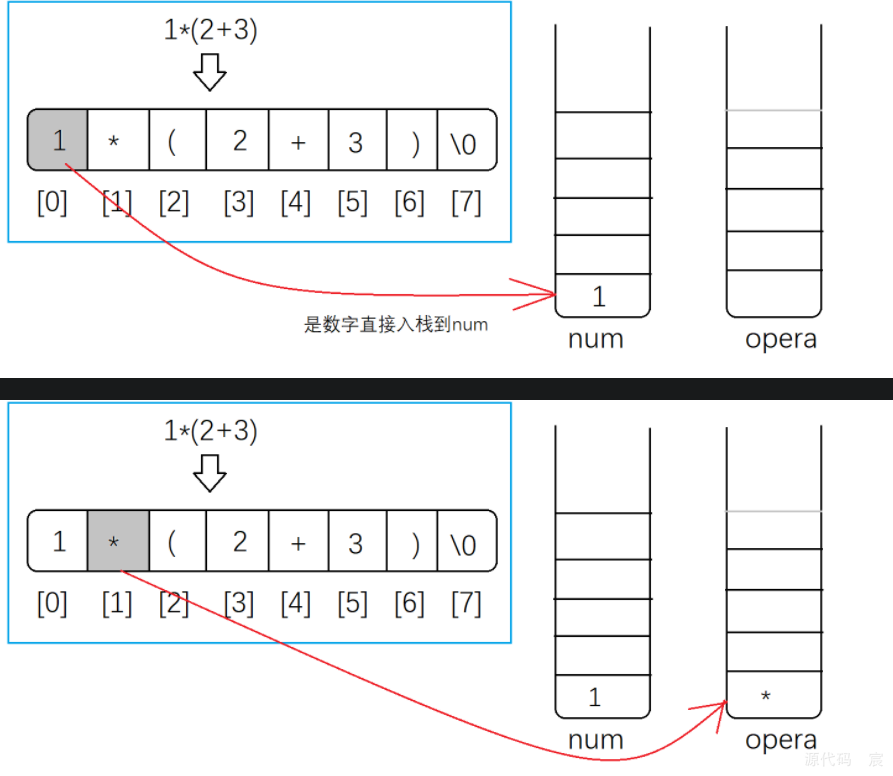
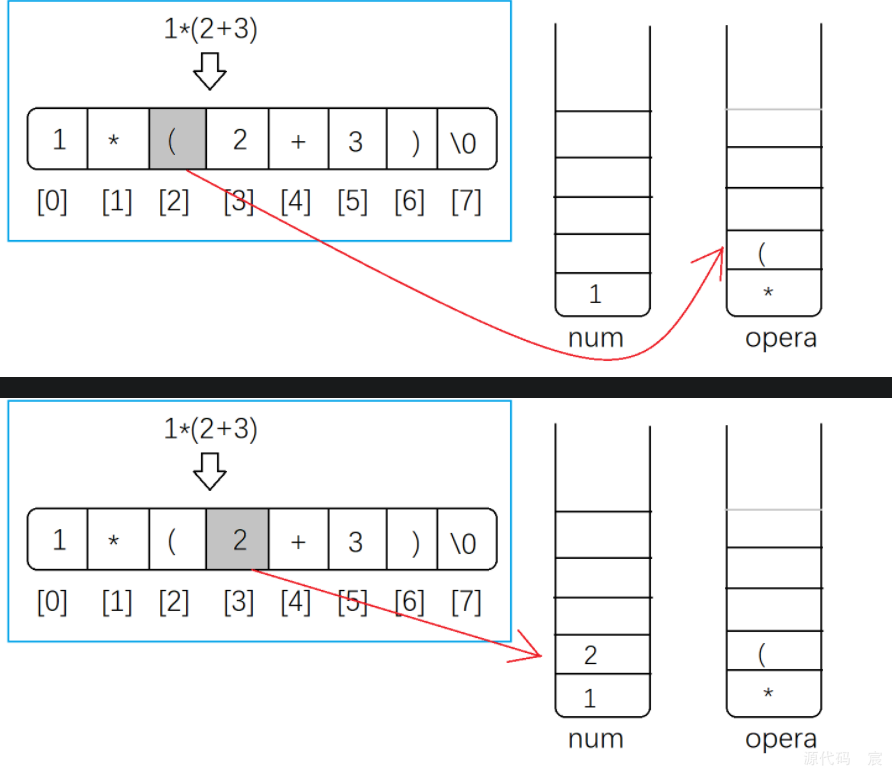



后缀表达式的计算







算法过程演示二
中缀表达式转换为后缀表达式











后缀表达式求值算法












尾声
本文参考了部分网络资源,便于提高文章的可读性

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








