面试经典算法题85-最大正方形

面试经典算法题85-最大正方形

公众号：阿Q技术站

LeetCode.221

问题描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

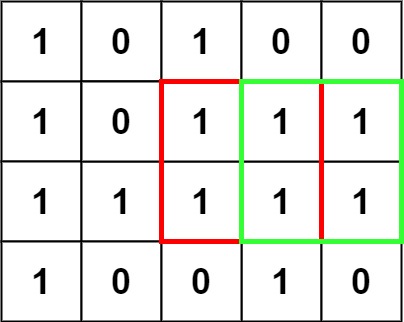
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

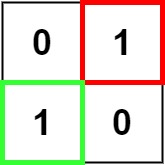
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

思路

1. 定义状态：使用一个二维数组 dp，其中 dp[i][j] 表示以 matrix[i][j] 为右下角的最大正方形的边长。

2. 状态转移方程：

   • 如果 matrix[i][j] 为 ‘1’，则 dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。

   • 如果 matrix[i][j] 为 ‘0’，则 dp[i][j] = 0。

3. 初始条件：第一行和第一列的 dp 值直接由 matrix 值决定。

4. 边界处理：

   • 矩阵为空时直接返回 0。

   • 遍历所有元素，更新最大边长。

5. 最终结果：用一个变量记录最大边长，最后返回其平方即为最大正方形的面积。

参考代码

C++

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int maximalSquare(vector<vector<char>>& matrix) {
    if (matrix.empty() || matrix[0].empty()) {
        return 0; // 如果矩阵为空，返回 0
    }

    int rows = matrix.size();
    int cols = matrix[0].size();
    vector<vector<int>> dp(rows, vector<int>(cols, 0)); // 初始化 dp 数组
    int maxSide = 0; // 用于记录最大的正方形边长

    // 遍历矩阵中的每一个元素
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            if (matrix[i][j] == '1') {
                if (i == 0 || j == 0) {
                    dp[i][j] = 1; // 如果是第一行或第一列，只能形成边长为 1 的正方形
                } else {
                    dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1; // 状态转移方程
                }
                maxSide = max(maxSide, dp[i][j]); // 更新最大边长
            }
        }
    }

    return maxSide * maxSide; // 返回最大正方形的面积
}

int main() {
    int rows, cols;
    cout << "输入矩阵行数: ";
    cin >> rows;
    cout << "输入矩阵列数: ";
    cin >> cols;

    vector<vector<char>> matrix(rows, vector<char>(cols));
    cout << "输入矩阵: \n";
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            cin >> matrix[i][j];
        }
    }

    int result = maximalSquare(matrix);
    cout << "最大正方形的面积: " << result << endl;

    return 0;
}

Java

import java.util.Scanner;

public class MaximalSquare {
    public static int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0; // 如果矩阵为空，返回 0
        }

        int rows = matrix.length;
        int cols = matrix[0].length;
        int[][] dp = new int[rows][cols]; // 初始化 dp 数组
        int maxSide = 0; // 用于记录最大的正方形边长

        // 遍历矩阵中的每一个元素
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1; // 如果是第一行或第一列，只能形成边长为 1 的正方形
                    } else {
                        dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1; // 状态转移方程
                    }
                    maxSide = Math.max(maxSide, dp[i][j]); // 更新最大边长
                }
            }
        }

        return maxSide * maxSide; // 返回最大正方形的面积
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.print("输入矩阵行数: ");
        int rows = scanner.nextInt();
        System.out.print("输入矩阵列数: ");
        int cols = scanner.nextInt();
        scanner.nextLine(); // consume newline

        char[][] matrix = new char[rows][cols];
        System.out.println("输入矩阵: ");
        for (int i = 0; i < rows; ++i) {
            String line = scanner.nextLine();
            for (int j = 0; j < cols; ++j) {
                matrix[i][j] = line.charAt(j);
            }
        }

        int result = maximalSquare(matrix);
        System.out.println("最大正方形的面积: " + result);
        scanner.close();
    }
}

Python

def maximalSquare(matrix):
    if not matrix or not matrix[0]:
        return 0  # 如果矩阵为空，返回 0

    rows, cols = len(matrix), len(matrix[0])
    dp = [[0] * cols for _ in range(rows)]  # 初始化 dp 数组
    max_side = 0  # 用于记录最大的正方形边长

    # 遍历矩阵中的每一个元素
    for i in range(rows):
        for j in range(cols):
            if matrix[i][j] == '1':
                if i == 0 or j == 0:
                    dp[i][j] = 1  # 如果是第一行或第一列，只能形成边长为 1 的正方形
                else:
                    dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1  # 状态转移方程
                max_side = max(max_side, dp[i][j])  # 更新最大边长

    return max_side * max_side  # 返回最大正方形的面积

# 测试代码
if __name__ == "__main__":
    matrix = [
        ["1", "0", "1", "0", "0"],
        ["1", "0", "1", "1", "1"],
        ["1", "1", "1", "1", "1"],
        ["1", "0", "0", "1", "0"]
    ]
    print("输入矩阵:")
    for row in matrix:
        print(row)
    result = maximalSquare(matrix)
    print("最大正方形的面积:", result)