第五章 循环结构程序设计

原创 于 2019-01-31 13:52:02 发布 · 401 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#第五章 循环结构程序设计

第五章 循环结构程序设计

例5.1 求1+2+3+…+100，即∑n。

#include<stdio.h>
int main()
{
int i=1,sum=0;                  //定义变量i的初值为1,sum的初值为0
while(i<=100)                   //当i>100,条件表达式i<=100的值为假，不执行循环体
{                               //循环体开始
sum=sum+i;                      //第1次累加后，sum的值为1
i++;                            //加完后,i的值加1，为下次累加做准备
}                               //循环体结束
printf("sum=%d\n",sum);         //输出1+2+3+...+100的累加和
return 0;
}

运行结果如下：
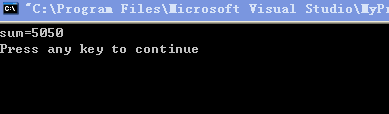
在这里插入图片描述

例5.2 用do…while语句求1+2+3+…+100，即∑n。

#include<stdio.h>
int main()
{
int i=1,sum=0;
do
[
sum=sum+i;
i++;
}while(i<=100);
printf("sum=%d\n",sum);
return 0;
}

运行结果如下：
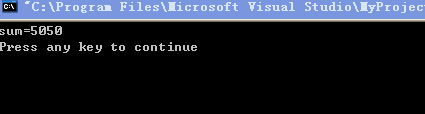
在这里插入图片描述

例5.3 while和do…while循环的比较。

(1)用while循环：

#include<stdio.h>
int main()
{
int i,sum=0;
printf("please enter i,i=?");
scanf("%d",&i);
while(i<=100)
{
sum=sum+i;
i++;
}
printf("sum=%d\n",sum);
return 0;
}

运行结果(两次）：

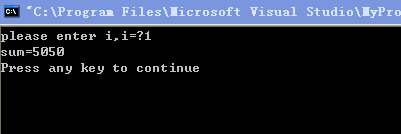
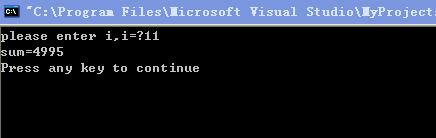
在这里插入图片描述

在这里插入图片描述
（2）用do…while循环：

#include<stdio.h>
int main()
{
int i,sum=0;
printf("please enter i,i=?");
scanf("%d",&i);
do
{
sum=sum+i;
i++;
}while(i<=10);
printf("sum=%d\n",sum);
return 0;
}

运行结果如下（两次）：
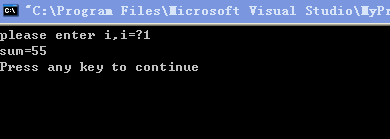
在这里插入图片描述
再运行一次：
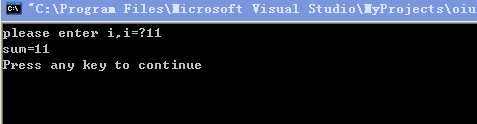
在这里插入图片描述

例5.4 在全系1000名学生中举行慈善募捐，当总数达到10万元时就结束，统计此时捐款的人数以及平时每人捐款的数目。

#include<stdio.h>
#define SUM 100000
int main()
{
float amount,aver,total;
int i;
for(i=1,total=0;i<=1000;i++)
{
printf("please enter amount:");
scanf("%f",&amount);
total=total+amount;
if(total>=SUM)break;
}
aver=total/i;
printf("num=%d\naver=%10.2f\n",i,aver);
return 0;
}

运行结果如下（为简化起见，只输入几个数据）：

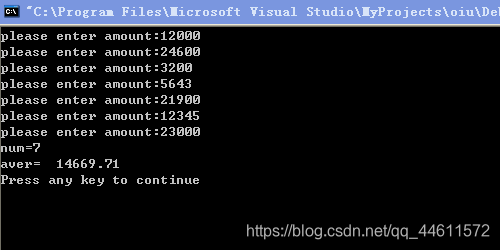
在这里插入图片描述

例5.5 要求输出100~200的不能被3整除的数。

#include<stdio.h>
int main()
{int n;
for(n=100;n<=200;n++)
{if(n%3==0)
continue;
printf("%d",n);
}
printf("\n");
return 0;
}

运行结果如下：

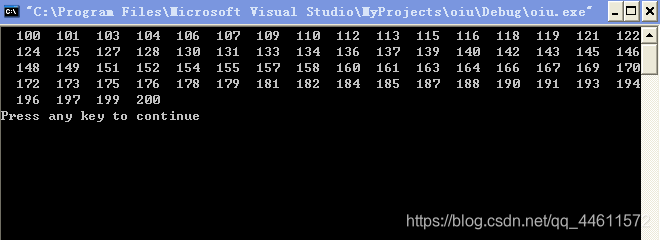
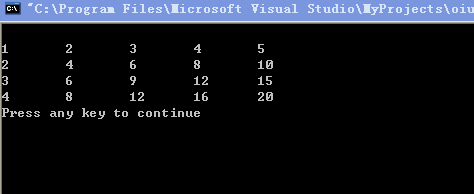
在这里插入图片描述

例5.6 输出以下4*5的矩阵。

                     1              2             3             4             5
                      2             4              6            8            10
                      3              6             9           12           15
                      4              8             12         16          20

#include<stdio.h>
int main()
{
int i,j,n=0;
for(i=1;i<=4;i++)
for(j=1;j<=5;j++,n++)
{if(n%5==0)printf("\n");
printf("%d\t",i*j);
}
printf("\n");
return 0;
}

运行结果如下：
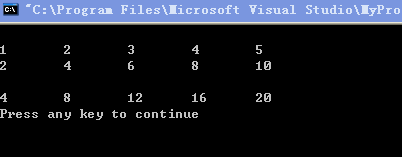
在这里插入图片描述
假如在以上程序的基础上作一些改动。在内循环体中增加一个if语句：
if(i3&&j1)break;
此时程序如下：

#include<stdio.h>
int main()
{
int i,j,n=0;
for(i=1;i<=4;i++)
for(j=1;j<=5;j++,n++)
{if(n%5==0)printf("\n");
if(i==3&&j==1)break;
printf("%d\t",i*j);
}
printf("\n");
return 0;
}

运行结果如下：
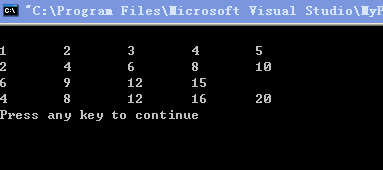
在这里插入图片描述
如果把上面的break语句改为continue语句，即：
if(i3&&j1)continue;

#include<stdio.h>
int main()
{
   int i,j,n=0;
   for(i=1;i<=4;i++)
   for(j=1;j<=5;j++,n++)
   {if(n%5==0)printf("\n");
   if(i==3&&j==1)continue;
    printf("%d\t",i*j);
   }
   printf("\n");
   return 0;
   }

运行结果如下：
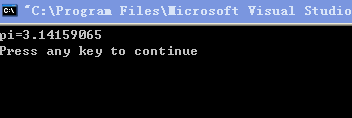
在这里插入图片描述

例5.7 用公式π/a≈1-1/3+1/5-1/7+…求π的近似值,直到发现某一项的绝对值小于10﹣6为止（该项不累加）。

#include<stdio.h>
#include<math.h>                        //程序中用到数学函数fabs，应包含头文件math.h
int main()
{
int sign=1;                             //sign用来表示数值的符号
double pi=0.0,n=1.0,term=1.0;           //pi开始代表多项式的值，最后代表π的值
                                        //term代表当前项的值
while(fabs(term)>=1e-6)                 //把当前项term的绝对值是否大于或等于10﹣6
{
pi=pi+term;                             //把当前项term累加到pi中
n=n+2;                                  //n+2是下一项的分母
sign=-sign;                             //sign代表符号，下一项的符号与上一项符号相反
term=sign/n;                            //求出下一项的值term
}
pi=pi*4;                                //多项式的和pi乘以4，才是π的近似值
printf("pi=%10.8f\n",pi);               //输出π的近似值
return 0;
}

运行结果如下：
在这里插入图片描述

例5.8 求Fibonacci（斐波那契）数列的前40个数。这个数列有如下特点：第1,2两个数为1,1。从第3个数开始，该数是其前面两个数之和。即该数列为1,1,2,3,5,8,13，…，用数学公式表示为

                              F1=1                        (n=1)
                              F2=1                        (n=2)
                              Fn=Fn-1+Fn-2         (n>=3)
      这是一个有趣的古典数学问题：有一对兔子，从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。假设所有兔子都不死，问每个月的兔子总数为多少？

#include<stdio.h>
int main()
{
int f1=1,f2=1,f3;
int i;
printf("%12d\n%12d\n",f1,f2);
for(i=1;i<=38;i++)
{
f3=f1+f2;
printf("%12d\n",f3);
f1=f2;
f2=f3;
}
return 0;
}

运行结果如下：
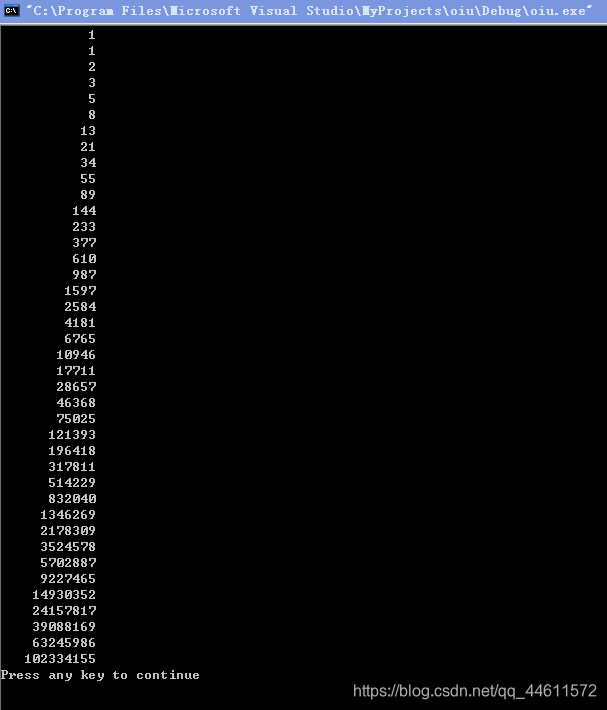
在这里插入图片描述
程序改进：可以修改程序，在循环体中一次求出下两个月的兔子数。而且只用两个变量f1和f2就够了，不必用f3。这里有一个技巧，把f1+f2的结果不放在f3中，而放在f1中取代了f1的原值，此时f1不再代表前两个月的兔子鼠，而代表新求出来的第3个月的兔子数，再执行f2+f1，由于此时的f1已是第3个月的兔子数，因此f2+f1就是第4个月的兔子数了，把它存放在f2中。可以看到此时的f1和f2已是新求出的最近两个月的兔子数。再由此推出下两个月的兔子数。

#include<stdio.h>
int main()
{int f1=1,f2=1;
int i;
for(i=1;i<=20;i++)
{
printf("%12d%12d",f1,f2);
if(i%2==0)printf("\n");
f1=f1+f2;
f2=f2+f1;
}
return 0;
}

运行结果如下：
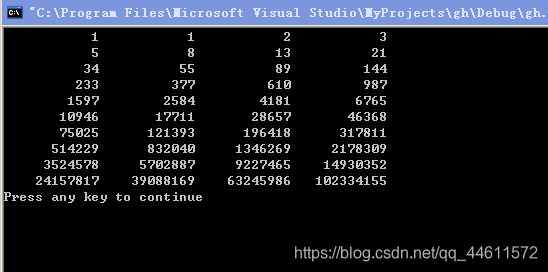
在这里插入图片描述

例5.9 输入一个大于3的整数你，判定它是否为素数（prime，又称质数）。

#include<stdio.h>
int main()
{int n,i;
printf("please enter a integer number,n=?");
scanf("%d",&n);
for(i=2;i<n;i++)
if(n%i==0)break;
if(i<n)printf("%d is not a prime number.\n",n);
else printf("%d is a prime number.\n",n);
return 0;
}

运行结果如下：

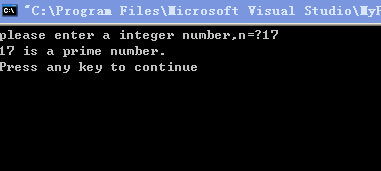
在这里插入图片描述
程序改进：其实n不必被2（n-1）的各整数去除，只须将n被2n/2的整数除即可，甚至只需被2√n的整数除即可。因为n的每一对因子，必然有一个小于√n，另一个大于√n。例如，判断17是否为素数，只须将17被2,3和4除即可，如都除不尽，n必为素数。这样做可以大大减少循环次数，提高执行效率。请读者思考为什么只须使n被2√n的整数除即可判定n是否为素数。
为方便，可以定义一个整型变量看（其值为√n的整数部分）；如果n不能被2看（即√n）的任意整数整除，则在完成最后一次循环后，i还要加1，因此i=k+1，然后才终止循环。在循环之后判别i的值是否大于或等于k+1，若是，则表明未曾被2k任意整数整除过，因此输出该数是素数。

#include<stdio.h>
#include<math.h>
int main()
{ int n,i,k;
printf("please enter a integer number,n=?");
scanf("%d",&n);
k=sqrt(n);
for(i=2;i<=k;i++)
if(n%i==0)break;
if(i<k)printf("%d is not a prime number.\n",n);
else printf("%d is a prime number.\n",n);
return 0;
}

运行结果如下：
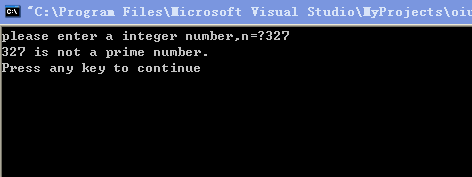
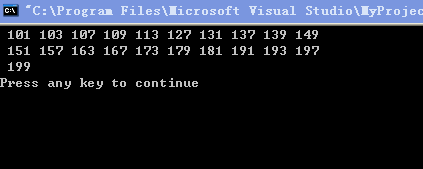
在这里插入图片描述

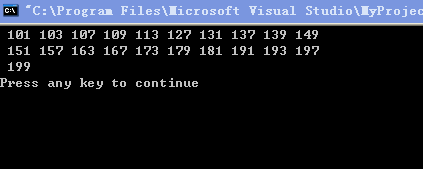
例5.10 求100~200的全部素数。

#include<stdio.h>
#include<math.h>
int main()
{int n,k,i,m=0;
for(n=101;n<=200;n=n+2)            //n从100变化到200，对每个n进行判定
{k=sqrt(n);
for(i=2;i<=k;i++)
if(n%i==0)break;                   //如果n被i整除，终止内循环，此时i<k+1
if(i>=k+1)                         //若i>=k+1，表示n未曾被整除
{printf("%4d",n);                  //应确定n是素数
m=m+1;                             //m用来控制换行，一行内输出10个素数
}
if(m%10==0)printf("\n");           //m累计到10的倍数，换行
}
printf("\n");
return 0;
}

运行结果如下：
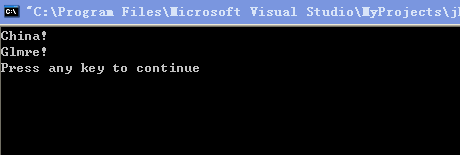
在这里插入图片描述

例5.11 从键盘输入一行字符，要求输出相应的的密码。

![#include<stdio.h>
int main()
{char c;
c=getchar();                                      //输入一个字符给字符变量
while(c!='\n')                                    //检查c的值是否为换行符'\n'
{if((c>='a'&&c<='z')||(c>='A'&&c<='Z'))           //c如果是字母
{if(c>='W'&&c<='Z'||c>='w'&&c<='z') c=c-22;       
                    //如果是26个字母中最后4个字母之一就使c-22
else c=c+4;         //如果是前面22个字母之一，就使c加4，即变成其后第4个字母
}
printf("%c",c);     //输出已改变的字符
c=getchar();        //再输入下一个字符给字符变量c
}
printf("\n");
return 0;
}](https://img-blog.csdnimg.cn/20190128192540196.)

运行结果如下：
在这里插入图片描述

冲呀冲鸭
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值