Java基础知识：Floyd算法

最新推荐文章于 2025-06-08 12:04:41 发布

空城老祖

最新推荐文章于 2025-06-08 12:04:41 发布

阅读量426

点赞数

CC 4.0 BY-SA版权

分类专栏：算法文章标签：算法数据结构 c++

本文链接：https://blog.youkuaiyun.com/qq_44579321/article/details/129477806

蓝桥杯同时被 2 个专栏收录

45 篇文章

订阅专栏

算法

22 篇文章

订阅专栏

Floyd-Warshall算法是一种用于求解图中任意两点间最短路径的算法，适用于有向图和无负权环的情况。它通过动态规划更新路径信息，使用三个嵌套循环来更新所有顶点对之间的最短路径。在Java代码示例中，展示了如何实现该算法并找到最短路径。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、介绍

Floyd-Warshall算法（英语：Floyd-Warshall algorithm），中文亦称弗洛伊德算法或佛洛依德算法，是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权（但不可存在负权回路）的最短路径问题。

2、原理

弗洛伊德算法先定义了两个二维矩阵：

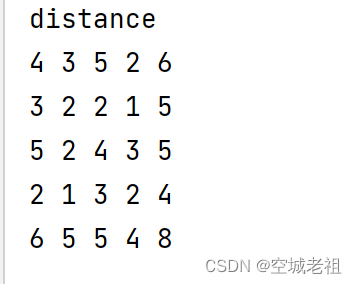
矩阵distance记录顶点间的最小路径例如distance[2][1]= 12，说明顶点2 到 1 的最短路径为12；
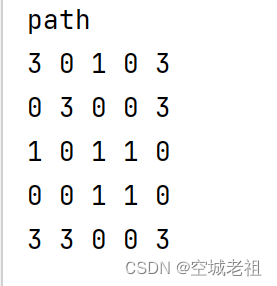
矩阵pre记录顶点间最小路径中的前驱节点例如pre[2][1]= 0 说明，2 到 1的最短路径轨迹经过0，1的前驱节点为 0；

tips : 输出具体路径的方法是从终点开始循环迭代起点那一行的pre数组的列下标，把列下标放进栈中，直到列下标等于起点。然后打印栈。例如打印distance[2][1]的路径，就循环迭代pre[2][1] 到 pre[2][2]，如下所示pre[2][1] --> pre[2][0] --> pre[2][2] 那么2到1的路径就越是 2 --> 0 --> 1

pre[2][1] == 0 pre[2][0]==2 pre[2][2]=2

3、代码

    public static int[][] floyd(int[][] distance,int v){
        int[][] path = new int[v][v];
        for (int k = 0; k < v; k++) {
            for (int i = 0; i < v; i++) {
                for (int j = 0; j < v; j++) {
                    //这段判断是否等于Integer.MAX_VALUE的代码必须写上，因为它是javaint的极限，随便加1都会导致值为负数
                    if (distance[i][k]!=Integer.MAX_VALUE&&distance[k][j]!=Integer.MAX_VALUE) {
                        if (distance[i][k]+distance[k][j]<distance[i][j]) {
                            distance[i][j] = distance[i][k]+distance[k][j];
                            path[i][j] = k;
                        }
                    }
                }
            }
        }
        return distance;
    }

测试

public static void main(String[] args) {
        int MAX_INT = Integer.MAX_VALUE;
        int[][] distance = {
                {MAX_INT, 3, MAX_INT, 2, MAX_INT},
                {3, MAX_INT, 2, 1, MAX_INT},
                {MAX_INT, 2, MAX_INT, MAX_INT, 5},
                {2, 1, MAX_INT, MAX_INT, 4},
                {MAX_INT, MAX_INT, 5, 4, MAX_INT}
        };
        int[][] dis = floyd(distance,5);
        for (int i = 0; i < 5; i++) {
            for (int j = 0; j < 5; j++) {
                System.out.print(dis[i][j]+" ");
            }
            System.out.println();
        }
}