读书笔记 --- 数据结构与算法分析C语言描述 --- 12.24 --- Chapter4 树 page76 - 79

4.3.5 delete

结点情况	对应解决方案
没有任何儿子的结点	此结点为BST中的叶结点，直接删除
仅有一个儿子的结点	类似于一个链表：grandfather->father->children中删除掉father结点的操作
有两个儿子的结点	找到右子树最小的结点代替被删除的结点，这个最小的结点为右子树中最左边的元素，因为最小的那个元素一定不会再有左儿子(当然也可以找左子树中最大的那个结点)，然后改变指针指向的过程就类似于上面所说的仅有一个儿子的结点的解决方案

BinarySearchTreeNode *T delete__(elem X, BinarySearchTreeNode *T) {
	BinarySearchTreeNode *temp;
	
	if ( T == nullptr ) 
		NotFoundError("Element doesn't exist!");
	
	// 先把X找到，利用递归进行查找，上面是基准情形
	else if ( X < T->elem ) 
		T->left = delete__(X, T->left);
	else if ( X > T->elem ) 
		T->right = delete__(X, T->right);
	// 属于有两个儿子的结点，找到右子树中最小的元素，将删除结点的elem换成temp的elem值并重接其右子树
	else if ( T->left != nullptr && T->right != nullptr ) {
		temp = findMin(T->right);
		T->elem = temp->elem;
		T->right = delete__(T->elem, T->right);
	}
	// 有一个或没有孩子的结点，没有孩子的结点将T直接删除(变成nullptr)，有一个孩子的结点有哪个孩子就将哪个孩子移上来
	else {
		temp = T;
		if ( T->left == nullptr )
			T = T->right;
		else if ( T->right == nullptr )
			T = T->left;
		free(temp);
	}

	return T;
}

一样的，我还是将课本上的代码做一个分析并放在这里帮助大家理解：



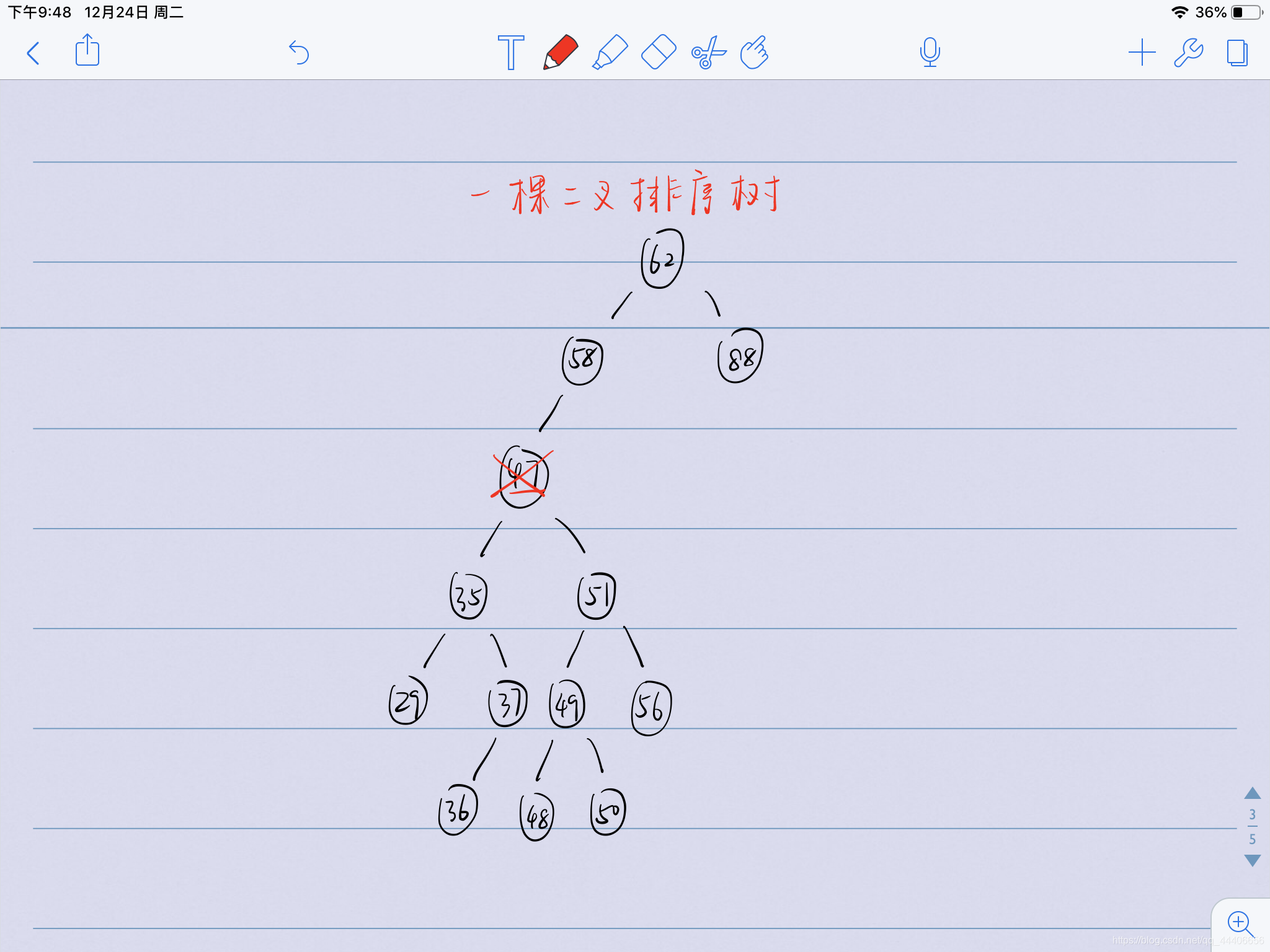
可以结合代码一起理解，我又运用了想象力进行了编程：

bool deleteBST(BiTree *T, int key) {
	if ( !*T ) 
		return false;
	else {
		if ( key == (*T)->data )
			return deleteNode(T);
		else if ( key < (*T)->data ) 
			return deleteBST(&(*T)->lchild, key);
		else
			return deleteBST(&(*T)->rchild, key);
	}
}

// 从二叉排序树中删除结点p并重接其左右子树
bool deleteNode(BiTree *p) {
	// s理解为一个探索指针，q在下面重接左/右子树的判断上发挥了作用
	BiTree q, s;
	// 前面只有一个孩子的就不再解释了，另外这个里面已经囊括了没有孩子的情况，不信你仔细看
	if ( (*p)->rchild == nullptr ) {
		q = *p;
		*p = (*p)->lchild;
		free(q);
	}
	else if ( (*p)->lchild == nullptr ) {
		q = *p;
		*p = (*p)->rchild;
		free(p);
	}
	// 这里我采用了找到左子树中最大的结点的方法
	else {
		// s进入左子树这边森林区域，藏宝图指示他刚进了森林就一直往右走
		q = *p;
		s = (*p)->lchild;

		while ( s->rchild ) {
			q = s;
			s = s->rchild;
		}
		// 元素进行替换
		(*p)->data = s->data;
		// 重接左/右子树
		if ( q != *p ) 
			q->rchild = s->lchild;
		else
			q->lchild = s->lchild;

		free(s);
	}
}

方案二代码留给大家去写(务必要动手尝试一下)，如果你真的看懂了我上面的讲解，那真的很容易。放个答案给你们参照一下

else {
	q = *p;
	s = (*p)->rchild; // 来到右子树这片森林

	while ( s->lchild ) {
		q = s;
		s = s->lchild;
	}
	
	(*p)->data = s->data;
	
	// 自己写代码时画个图对重接左/右子树进行判断，断不能死记硬背。
	if ( q != *p )
		q->lchild = s->rchild;
	else
		q->rchild = s->rchild;

	free(s);
}

好，现在回到我们最初所给出的代码上来。我们发现这个程序的效率并不高，他沿着树进行了两趟搜索，查找并删除了右子树最小的结点。那么解决方案是什么呢？没错，我们可以写一个特殊的deleteMin()函数。

然后在这里介绍一个重要的策略：懒惰删除(lazy deletion)。若删除次数不多，我们通常都可以使用这个策略。**当一个元素要被删除时，他仍留在树中，只是做了个被删除的记号。**这个策略有时可以帮我们节省很多开销。因为我们在对一个元素进行完全删除时，片外索引值需要做出相应调整，动态元素集难以接受这样的开销。而用一个flag片记录片外元素状态，1表示删除状态，0表示未删除状态。当有元素的状态被设置为1，变成了删除状态，而其他片外索引值不变。因此这个策略在删除重复关键字时使用是非常合理的。

4.3.6 平均情形分析

我们一开始的期望是之前所有操作均花费O(log N)时间，而实际上除了makeEmpty()外，所有的操作看似均花费了O(d)(d为访问关键字结点深度)。因此下面证明假设所有树出现机会均等，树中所有结点平均深度为O(log N)。
一棵树所有结点深度和成为内部路径长(internal path length)。我们现在的思路是二叉查找树平均内部路径长，则我们现在令D(N)是具有N个结点的某棵树T的内部路径长，一棵N结点的树由$i$个结点的左子树以及$N-i+1$个结点的右子树以及深度为0的一个根结点组成。D($i$)为左子树内部路径长，但是在原来的树中，所有这些结点都要加深一度。(受根结点影响)。此结论同样适用于右子树，于是我们得到下面的递归关系：

D(N) = D($i$) + D($N-i+1$) + N - 1

若所有子树大小都等可能出现，而这对于二叉查找树则是成立的。然而对于二叉树并不成立，于是得出D($i$)和D($N-i+1$)的平均值均为
(1 / N) ${\sum }_{j=0}^{N-1}D(j)$，即：

D(N) = (2 / N) ${\sum }_{j=0}^{N-1}D(j)$ + N - 1

得出平均值为D(N) = O(N log N)