指针分析-改进版Andersen算法（一）_pointer analysis andersen-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_44370676/article/details/124236109

Wave Propagation and Deep Propagation for Pointer Analysis

一.背景
二.Wave Propagation
三.Deep Propagation
- 3.1.算法
- 3.2.示例
四.实验
五.总结
六.SVF实现
七.参考文献

这篇paper提出了2个Andersen-based指针分析算法，这里的改版同样是field-insensitive的

Wave Propagation Method：这是PKH $^{[2]}$ 算法（一种Andersen算法改版）的升级版。Wave Propagation Method相比PKH算法提升了时间效率。
Deep Propagation Method：一种更加轻量级的分析算法。

SVF中已有Wave Propagation算法的实现：AndersenWaveDiff类

一.背景

如果2个变量的存储空间可能重叠，那么这2个变量存在别名关系。现在已经有许多类型的指针分析算法，这里主要关注flow-insensitive以及context-insensitive的算法。主要以Andersen算法和Steensgard算法为主。在前一篇中我简单介绍了Andersen算法以及SVF中的实现。

尽管flow & context-sensitive算法精度更高，但是通常flow & context-insensitive提供的精度已经足够，比如GCC和LLVM就使用 inclusion-based flow & context-insensitive算法。

在用Andersen算法进行指针分析时，可能会出现如下情况：

p = &a;
q = p;
r = q;
p = r;

约束图如下：

在这里插入图片描述
可以看到 p, q, r 形成 copy 环路，pts 集永远一样，因此在实际运用中如果能提前识别环路并进行压缩能极大提高效率。环路即有向图的强连通分量。在压缩环路上已有的工作有（部分列举）：

Lazy Cycle Detection and Hybrid Cycle Detection $^{[3]}$ （SVF中对应AndersenLCD和AndersenHCD）
Pearce等人提出的PKH算法 $^{[4]}$

二.Wave Propagation

Wave Propagation本身是PKH算法 $^{[2]}$ 的一个改版（之后会介绍PKH算法），Andersen-style算法主要包括更新约束图结点（变量）的 pts 集（只增不减）和添加 copy 边。

2.1.Wave Propagation

这个Wave Propagation运行流程如下：

在这里插入图片描述循环体中包含3个步骤：

将强连通分量压缩（collapse）为1个结点
实施Wave Propagation（针对 copy 边更新 pts 集）
通过复杂约束（store, load 等）添加新的 copy 边

当没有新 copy 边被添加时退出循环，可以看到Propagation添加边之前，应该是考虑到添加边可能会引入新的环从而对Propagation造成不便。

2.2.压缩强连通分量

作者采用了Nuutila等人 $^{[5]}$ 的算法来查找强连通分量，这是Tarjan算法的升级版。

算法主体为下图的算法2，算法2调用了算法3来计算强连通分量，整个算法中用到了以下变量，整个算法基于深度优先遍历算法改进，每个结点只被访问一次：

$\mathcal{D}$ ：用来将结点 $v$ 映射到其访问顺序， $\mathcal{D}(v) = 4$ 表示结点 $v$ 第4个被访问，初始化为 Nan。
$\mathcal{R}$ ：将结点 $v$ 映射到其所在强连通分量的代理结点（representative of that cycle），初始化 $\mathcal{R}(v) = v$ 。
$\mathcal{C}$ ：保存约束图中所有成环的结点，初始化为 $\varnothing$ 。
$\mathcal{T}$ ：为1个栈，按拓扑序保存约束图中所有的强连通分量（强连通分量可以只包含结点自身）。
$\mathcal{S}$ ：中间变量，为1个栈，保存成环的结点，初始化为空。

在这里插入图片描述

我以下面例子为例：

在这里插入图片描述
在算法2运行到第3行时:

$\mathcal{D} = \{A: 1, B: 2, C: 3, D: 4, E: 8, F: 5, G: 6, H: 7\}$
$\mathcal{R} = \{A: A, B: B, C: B, D: D, E: E, F: D, G: D, H: H\}$
$\mathcal{C} = \{G, F, D, B, C\}$
$\mathcal{T} = \{E, A, H, B, D\}$

2.3.实施Wave Propagation

Wave Propagation的伪代码如下：

在这里插入图片描述这里 $\Tau$ 相当于前一篇中的Worklist，不过 $\Tau$ 的结点按拓扑序弹出。这里跟普通的Andersen算法更新时很像，区别在于每个结点保存2个 pts 集， $p_{cur}$ 和 $p_{old}$ 。前者保存该结点当前的 pts 集，算法结束迭代时 $p_{cur}$ 就是最终分析结果，后者保存上一次迭代后的 pts 集。在更新时，也会计算差值，通过差值更新，不过没有本质区别。

2.4.添加新边

在这里插入图片描述
在前一篇提到的Andersen算法中，添加新边（下图蓝框）和Propagation（下图红框）是放在一起（针对每个结点进行）没有分离的，而这里作者将这2个过程分离。添加边的时候并没有考虑将同一个结点对应的约束（load、store）放到一起处理。

而这里引入了一个新的 pts 集 $p_{cache}(c)$ 对应约束 $c$ 的 pts 集。这里的约束包括了 load, store 类。 $p_{cache}(l = *r)$ 与 $p_{cur}(r)$ 同步， $p_{cache}(*l = r)$ 与 $p_{cur}(l)$ 同步。引入 $p_{cache}(c)$ 主要是为了在约束求解时只考虑 pts 集中新添加的结点，提高效率。

请添加图片描述

2.5.motivating example

以如下代码为例：

H = &C 
E = &G 
B = C
H = &G 
H = A 
C = B
A = &E 
F = D 
B = A
D = *H 
*E = F 
F = &A

这里约束图中只画出 copy 边， addr, load, store 都没有画在里面。约束图和 $P_{cur}$ 变化如下gif所示：

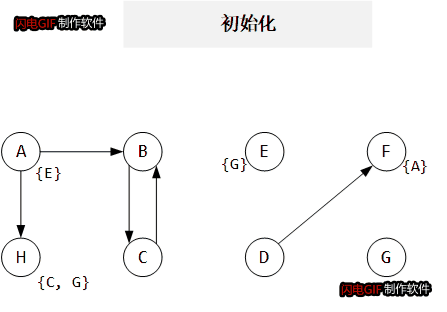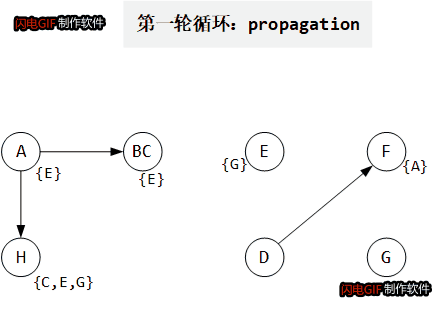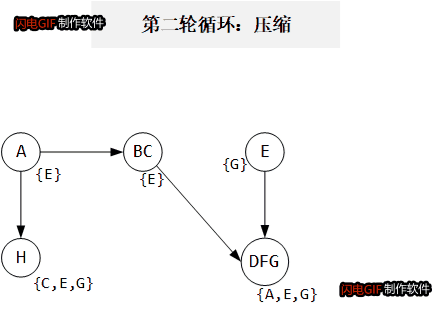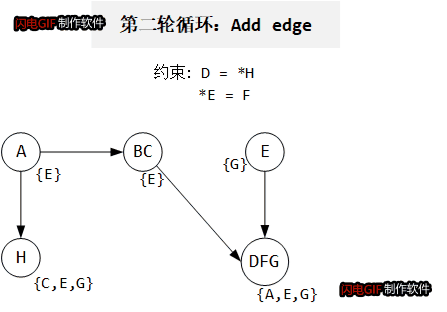
请添加图片描述

算法复杂度：

压缩环路（强连通分量）的复杂度为 $O(V^2)$ （ $V$ 为结点数）
wave propagation和插入新边的复杂度为 $O(V^3)$

三.Deep Propagation

Wave Propagation算法非常占用内存。因此作者还提出了改进版算法Deep Propagation，伪代码如下：

3.1.算法

在这里插入图片描述
这里同样用到了前面的压缩结点和Wave Propagation，区别是这2个步骤只执行一次，主体循环只包括添加边（求解 load 和 store 约束），pts 的更新通过Deep Propagation（上图16、26行）执行。

Deep Propagation的主要思想是给定结点 $v$ ，一个变量集合 $P_{dif}$ （包含即将添加进 $P_{cur}(l)$ 的变量），算法会将 $P_{dif}$ 中的变量添加到 $v$ 以及约束图中 $v$ 可达结点的 pts 集合中，用到了递归深度优先遍历。深度优先遍历会更新所有结点的 pts 集并搜寻环路。

上述算法6中，包括2个部分：

load 约束（ $\supseteq *r$ ）：首先针对结点 $l$ 计算 $P_{dif}$ ，从算法6第15行可以看出 $P_{dif}$ 中包含的是即将添加进但尚不在 $P_{cur}(l)$ 中的结点，此后将 $P_{dif}$ 沿以 $l$ 为起点的路径进行传播（Deep Propagation，传播之前已经添加了约束 $c$ 对应的 copy 边）。
store 约束（ $\supseteq r$ ）：与 load 类似，不过 store 中Deep Propagation发生在二重循环内而 load 中发生在一重循环内。

上述算法中 $P_{new edges}$ 、 $P_{cache}(c)$ 的引入均是为了减少重复计算，两种约束对应的示例可参考下图，左边对应 load，右边对应 store，红色边对应Deep Propagation对应的路径，load 中1个约束只执行1次Deep Propagation而 store 中可能执行多次。

在下图示例中

对于左图 load 情况，算法首先计算出了 $P_{dif}(l) = \{a, b\}$ ，之后DP算法会从 $l$ 开始深搜，更新路径上结点的 pts 集，同时试图搜索一个回到 $l$ 的环路。
对于右图 store 情况，算法求得了 $pts(l) = \{p, q\}$ ，之后计算出了 $P_{dif}(p) = \{a\}, P_{dif}(q) = \{b\}$ ，然后分别从 $p, q$ 开始深搜，修改所有遍历过得结点的 pts 集并试图搜索一个回到 $r$ 的环路（虚线）。

在这里插入图片描述

Deep Propagation（算法7）伪代码如下：

在这里插入图片描述
算法7是基于深度优先递归的算法，有点绕，输入遍历包括3个：

Deep Propagation起始结点 $v$ 。
需要更新的结点集合 $P_{dif}$ 。
停止点 $s$ ：并不是以 $v$ 为起始点的路径上所有结点都需要遍历，有的结点的 pts 集可能已经包含 $P_{dif}$ （环路情况，压缩算法只执行了一次，因此添加Copy边可能引入新的环路），因此可以提前终止。

作者在这里会给结点进行上色操作：

凡是深搜遍历过的结点都会被上色，该更新 pts 集的更新 pts 集。
当存在起始点 $v$ 到停止点的路径时， $v$ 会被标为灰色。所有的灰色结点为环路上的结点，之后会压缩。
不存在路径 $v$ 会被标为黑色。也就是说黑色的结点都不在环路上，可以无视。

上色操作是动态变化的，同一个结点可能先变黑后有变无色。

3.2.示例

第二部分用到的示例在Deep Propagation中的状态变化如下：

在这里插入图片描述

在求解 load 约束 $D = * H$ 时，起始点和停止点均为 $D$ ， $P_{dif} = \{E, G\}$ ，处理完之后的结果如上图第2部分所示， $F$ 点被标为黑点，表示遍历过 F 但是不在环路上。
处理 store 约束 $* E = F$ 时，算法添加了 copy 边 $\rightarrow G$ ，此时 $F, G, E$ 形成环路。进行Deep Propagation时起始点为 $G$ ，停止点为 $F$ ， $P_{dif} = \{A, E, G\}$ 。算法迭代结束后 $D, G$ 被标为灰色，表示找到了环路，此时算法6会将 $F$ 和2个灰色结点 $G, D$ 压缩为1个结点。

显然，算法6在第一次用Nuutila算法压缩环路后，之后都是动态地压缩环路，这种方式提高了效率但是并不一定能消除约束图中所有的环路。

在这里插入图片描述
在求解 $* Y = A$ 的时候会添加边 $\rightarrow B$ ，此时 $A, B, C, E$ 构成环路。此时Deep Propagation被调用， $P_{dif} = \{X\}$ 、起始点为 $B$ 、停止点为 $A$ 。但是在计算点 $C$ 时，算法7的第7行的条件为 false，并且不存在边 $\rightarrow A$ ，因此 $C$ 被标为黑色，环路并没有被求解出。算法只有在 $P_{new}$ 不为空的时候才会找出环路。

算法的复杂度为 $O(V^3)$

四.实验

对比方法包括下面几个：

Lazy Cycle Detection $^{[3]}$ ：该算法只要在结点 $v$ 和后继结点 $w$ 的 pts 集相等时才寻找环路。
HT算法 $^{[6]}$
PKH算法 $^{[2]}$ ：GCC中应用的指针分析算法，它依赖于约束图必须拓扑排序好，以避免在整个节点空间中搜索时碰到环路情况。

作者用GCC中的 bitmap 数据结构来表示 pts 集，作者从下面几个方向进行对比。

4.1.渐近性

为了评估这些算法的稳定性和渐进性，作者选取了216个随机的约束图进行测试，这些约束图是根据实际程序的约束图随机生成的，这些生成的约束图和实际程序的约束图有一定差距。这里主要衡量实际运行时间跟约束数量的关系是否符合复杂度关系。

结果如下图所示：

在这里插入图片描述
结果表示Wave Propagation的稳定性和渐进性最好。

4.2.运行时间

衡量算法的运行时间，这里用到的数据集中是 $[3]$ 中提出的benchmark，包含了SPEC 2000中的6个大型程序。benchmark信息如下表所示，第二列是short name。

由于算法是field-insensitive的，所有的对比算法也调整为field-insensitive的。

在这里插入图片描述
对比试验的结果如下图所示，运行时间的单位以HT算法的运行时间为基本单位。比如ex在Intel running MacOSX setting中，DP的运行时间不到1，意味着DP此时的运行时间小于HT的，而其它3中算法的运行时间大于1，意味着这些算法运行时间大于HT的。

在这里插入图片描述
在算法各个部分花销占比如下图所示，大部分时间都花在Add Edge中：

在这里插入图片描述

4.3.内存占用

内存占用依旧以HT的内存占用指标为单位，结果如下：

在这里插入图片描述可以看出在大部分情况下WP算法的内存花费高于其它几种算法。

五.总结

作者提出了WP和DP算法提高了现有的context & flow & field-insensitive指针分析算法的效率：

环路消除使约束求解（point-to solver）的并行化变得复杂，因为这种优化可能会强制锁定约束图中一定数量的节点，以避免数据竞争。WP算法分离了压缩环路和约束求解过程减轻了数据竞争问题。
DP算法针对WP算法做了进一步优化，提高了时间和空间效率。

与原始context & flow & field-insensitive Andersen算法相比，WP算法在其基础上加上了压缩环路，并且在解析约束（load, store, copy）时用到了更多中间变量减少重复计算。

六.SVF实现

SVF实现参考AndersenWaveDiff 。SVF中的Andersen算法继承关系如下：

6.1.算法大致流程

SVF中Andersen算法大致流程是：构造函数 -> initialize -> initWorklist -> solveWorklist（处在循环体内）（后面3个包括在 analyze 函数中）

对于 analyze 方法 AndersenWaveDiff 继承自 AndersenBase，当Andersen算法将 reanalyze 标志设置为 true 时算法会循环进行。在大部分Andersen算法中 reanalyze 恒为 false，因此 solveWorklist 只执行了一次，而论文中算法1伪代码包含 while True，因此 AndersenWaveDiff 存在设置 reanalyze = true 的语句（目测在 processLoadStore）中。
对于 initialize 方法 AndersenWaveDiff 继承自Andersen，该方法主要内容是 processAllAddr，即初始化的时候处理 a = &c; 这类情况，将 c 添加进 pts(a)。
initWorklist 继承自Andersen，为空。
AndersenWaveDiff 自己实现了solveWorklist，代码如下：

void AndersenWaveDiff::solveWorklist()
{
    // Initialize the nodeStack via a whole SCC detection
    // Nodes in nodeStack are in topological order by default.
    NodeStack& nodeStack = SCCDetect();

    // Process nodeStack and put the changed nodes into workList.
    while (!nodeStack.empty())
    {
        NodeID nodeId = nodeStack.top();
        nodeStack.pop();
        collapsePWCNode(nodeId);
        // process nodes in nodeStack
        processNode(nodeId);
        collapseFields();
    }

    // This modification is to make WAVE feasible to handle PWC analysis
    if (!mergePWC())
    {
        NodeStack tmpWorklist;
        while (!isWorklistEmpty())
        {
            NodeID nodeId = popFromWorklist();
            collapsePWCNode(nodeId);
            // process nodes in nodeStack
            processNode(nodeId);
            collapseFields();
            tmpWorklist.push(nodeId);
        }
        while (!tmpWorklist.empty())
        {
            NodeID nodeId = tmpWorklist.top();
            tmpWorklist.pop();
            pushIntoWorklist(nodeId);
        }
    }

    // New nodes will be inserted into workList during processing.
    while (!isWorklistEmpty())
    {
        NodeID nodeId = popFromWorklist();
        // process nodes in worklist
        postProcessNode(nodeId);
    }
}

首先这和论文原算法已经有些出入：

首先通过 NodeStack& nodeStack = SCCDetect(); 进行连通分量检测，相当于算法2。nodeStack 相当于变量 $\mathcal{T}$ 。
while (!nodeStack.empty()) 中的语句块相当于算法4，这里暂时忽略 collapsePWCNode 和 collapseFields 函数，这2个函数与field有关，论文算法是field-insensitive的。可以看到算法4循环主体部分由 processNode(nodeId) 完成。这里 nodeId 对应算法4中的 $v$ 。

原论文Wave Propagation算法伪代码：

在这里插入图片描述

SVF版本的算法1伪代码如下：

在这里插入图片描述

6.2.算法4

算法4实现Wave Propagation，对应processNode 的代码如下：

void AndersenWaveDiff::processNode(NodeID nodeId)
{
    // This node may be merged during collapseNodePts() which means it is no longer a rep node
    // in the graph. Only rep node needs to be handled.
    if (sccRepNode(nodeId) != nodeId)
        return;

    double propStart = stat->getClk();
    ConstraintNode* node = consCG->getConstraintNode(nodeId);
    handleCopyGep(node);
    double propEnd = stat->getClk();
    timeOfProcessCopyGep += (propEnd - propStart) / TIMEINTERVAL;
}

handleCopyGep代码如下：

void AndersenWaveDiff::handleCopyGep(ConstraintNode* node)
{
    NodeID nodeId = node->getId();
    computeDiffPts(nodeId);

    if (!getDiffPts(nodeId).empty())
    {
        for (ConstraintEdge* edge : node->getCopyOutEdges())
            if (CopyCGEdge* copyEdge = SVFUtil::dyn_cast<CopyCGEdge>(edge))
                processCopy(nodeId, copyEdge);
        for (ConstraintEdge* edge : node->getGepOutEdges())
            if (GepCGEdge* gepEdge = SVFUtil::dyn_cast<GepCGEdge>(edge))
                processGep(nodeId, gepEdge);
    }
}

computeDiffPts(nodeId) 对应 $P_{cur}(v) − P_{old}(v)$

暂时忽略 processGep（field-insensitive还不用关注），ProcessCopy代码如下：

bool AndersenWaveDiff::processCopy(NodeID node, const ConstraintEdge* edge)
{
    numOfProcessedCopy++;

    bool changed = false;
    assert((SVFUtil::isa<CopyCGEdge>(edge)) && "not copy/call/ret ??");
    NodeID dst = edge->getDstID();
    const PointsTo& srcDiffPts = getDiffPts(node);
    processCast(edge);
    if(unionPts(dst,srcDiffPts))
    {
        changed = true;
        pushIntoWorklist(dst);
    }

    return changed;
}

srcDiffPts/getDiffPts(node) 对应 $P_{dif}$
dst 对应 $\omega$
unionPts(dst,srcDiffPts) 对应 $P_{cur}(\omega) = P_{cur}(\omega) \cup P_{dif}$
同时，这里对算法4做了1点小改进，添加了以下伪代码

$\;\;P_{cur}(\omega) \;\; change: \\ push(\omega)$

在这里插入图片描述

6.3.算法5

SVF对算法5做了一点小调整，用 tmpWorklist 保存了一个Worklist 副本，之后将 Worklist 重新赋值为 tmpWorklist。目的就是按拓扑序处理约束图结点的 Store 和 Load 边。相关代码由postProcessNode完成:

void AndersenWaveDiff::postProcessNode(NodeID nodeId)
{
    double insertStart = stat->getClk();

    ConstraintNode* node = consCG->getConstraintNode(nodeId);

    // handle load
    for (ConstraintNode::const_iterator it = node->outgoingLoadsBegin(), eit = node->outgoingLoadsEnd();
            it != eit; ++it)
    {
        if (handleLoad(nodeId, *it))
            reanalyze = true;
    }
    // handle store
    for (ConstraintNode::const_iterator it = node->incomingStoresBegin(), eit =  node->incomingStoresEnd();
            it != eit; ++it)
    {
        if (handleStore(nodeId, *it))
            reanalyze = true;
    }

    double insertEnd = stat->getClk();
    timeOfProcessLoadStore += (insertEnd - insertStart) / TIMEINTERVAL;
}

handleLoad代码如下：

bool AndersenWaveDiff::handleLoad(NodeID nodeId, const ConstraintEdge* edge)
{
    bool changed = false;
    for (PointsTo::iterator piter = getPts(nodeId).begin(), epiter = getPts(nodeId).end();
            piter != epiter; ++piter)
    {
        if (processLoad(*piter, edge))
        {
            changed = true;
        }
    }
    return changed;
}

processLoad 会进行添加边的操作并更新 pts 集，如果添加了新边，返回 True，否则 false。processStore类似。可以看出，SVF中算法5在有新边添加时，会将 reanalyze 标志设置为 True，以此循环往复。

不过SVF貌似并没有引入 $P_cache$ ， $P_old$ 这些差集，直接最简单粗暴的计算。

论文中的算法5流程如下：
在这里插入图片描述
SVF改版后流程如下（忽略Algorithm 2字样）：

在这里插入图片描述

七.参考文献

[1].Pereira F , Berlin D . Wave Propagation and Deep Propagation for Pointer Analysis[C]// International Symposium on Code Generation & Optimization. IEEE, 2009.
[2].Pearce D J , Kelly P H J , Hankin C . Efficient field-sensitive pointer analysis of C[J]. ACM Transactions on Programming Languages and Systems, 2007, 30(1):4.
[3] Hardekopf B , Lin C . The ant and the grasshopper: Fast and accurate pointer analysis for millions of lines of code[C]// Proceedings of the ACM SIGPLAN 2007 Conference on Programming Language Design and Implementation, San Diego, California, USA, June 10-13, 2007. ACM, 2007.
[4] Pearce D J , Kelly P , Hankin C . Online cycle detection and difference propagation for pointer analysis[C]// Source Code Analysis and Manipulation, 2003. Proceedings. Third IEEE International Workshop on. IEEE, 2003.
[5] Nuutila E , Soisalon-Soininen E . On finding the strongly connected components in a directed graph[J]. Information Processing Letters, 1994, 49(1):9-14.
[6] Nevin Heintze and Olivier Tardieu. Ultra-fast aliasing analysis using
CLA: A million lines of C code in a second. In PLDI, pages 254–263,
2001.