PyTorch中矩阵（二维张量）的线性代数运算

最新推荐文章于 2025-08-07 05:10:12 发布

原创

最新推荐文章于 2025-08-07 05:10:12 发布 · 3.5k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #矩阵 #机器学习 #张量 #深度学习

本文介绍了矩阵的基本运算，包括点积、矩阵乘法等，并详细阐述了矩阵的线性代数运算，如矩阵的迹、秩、行列式等概念。此外，还深入探讨了矩阵分解方法，包括特征分解和奇异值分解(SVD)，并解释了它们的实际应用。

1 矩阵的形变及特殊矩阵的构造方法

矩阵的形变其实就是二维张量的形变方法，在此基础上本节将补充转置的基本方法。实际线性代数运算过程中，一些特殊矩阵，如单位矩阵、对角矩阵等相关创建方法如下：

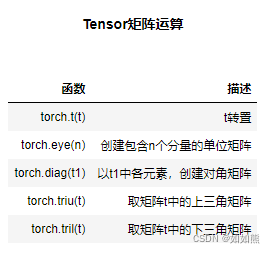
注：t1为一个矩阵，则 torch.t(t1) 与 t1.t()等效。

2 矩阵的基本运算

矩阵不同于普通的二维数组，其具备一定的线性代数含义，而这些特殊的性质，其实就主要体现在矩阵的基本运算上。常见的矩阵基本运算如下：

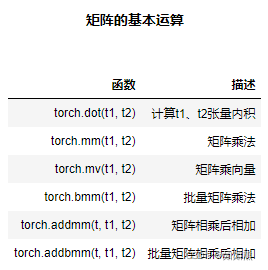
dot\vdot：点积计算。dot和

最低0.47元/天解锁文章

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

L_bloomer

关注关注

3
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
打赏
打赏
打赏举报

举报

Pytorch 二维张量常用方法

Mr数据杨

02-22

1万+

二维张量作为张量的重要类型之一，在处理图像数据、数据集转化及深度学习计算中扮演了重要角色。PyTorch 提供了便捷的操作方法，使得二维张量的创建、转换、索引、切片和运算更加高效直观。掌握这些基本操作，有助于深入理解深度学习模型的数据处理机制。

Pytorch-矩阵基本运算

Mr___WQ的博客

07-06

2374

pytorch入门，矩阵基本运算

参与评论您还未登录，请先登录后发表或查看评论

pytorch入门--矩阵基本运算

qq_43923588的博客

08-14

4497

本篇pytorch的矩阵基本运算进行展示，包含： add/subtract/multiply/divide matmul pow 次方 sqrt/rsqrt 次方根近似运算上下界操作使用方法和含义均在代码的批注中给出，因为有较多的输出，所以设置输出内容的第一个值为当前print()方法所在的行矩阵基本运算 import torch import numpy as np import sys loc = sys._getframe() _ = '\n' ''' add/subtract/m

torch 的 3种矩阵乘法运算

OrdinaryMatthew的博客

08-17

5899

说明 2 维 tensor 与 2 维 tensor，torch.matmul 函数也是执行矩阵乘法。会得到 torch.Size([1]) 而不是 torch.Size([])，Vec3 的 shape 是 torch.Size([])。结果和 torch.mm 计算出来的例 2 的结果一样的。注，输入的两个 tensor 的 shape 都是。当操作符是最最最自然的 “*” 时，执行的时。输出的 tensor 的shape 也是。的矩阵对应相乘，拼成一个。将 Mat1 修改为。.........

Pytorch张量的数学运算：矩阵运算

m0_63997099的博客

04-08

2638

矩阵的行列式是一个标量值，它提供了矩阵（线性变换）的一些重要性质的信息。对于一个方阵（即行数和列数相等的矩阵），其行列式可以通过多种方法计算，包括拉普拉斯展开、行列式的定义，或者更实用的方法，如LU分解。对于矩阵的运算有加、减、逐元素乘、数乘、点积（矩阵乘法）、逐元素除、转置、逆、行列式。向量的点积（也称为内积或标量积）和矩阵的点积（通常指矩阵乘法）在数学上有不同的定义和用途，因此它们的计算方式也不相同。计算矩阵的逆可以通过多种方法实现，包括代数余子式法（对于小的矩阵）、高斯消元法或LU分解等。

pytorch中矩阵计算的一些方法|优快云创作打卡

m0_61686427的博客

01-18

2608

李沐老师线性代数那一章的总结一、平均数二、广播机制三、某个轴计算A的累加求和四、求矩阵点积五、求一个矩阵和一个向量的乘积六、求矩阵的乘积七、求向量范数八、求矩阵的范数一、平均数 1.先生成A 2.进行平均数的运算 Mean函数就是一个求平均值的函数，也可以表示为A.sum()/A.numel()，numel函数求得A中元素的个数。此外还可以单独对某一个维度求平均数，也是有两种方法，其中shape[0]是指第一个维度元素的个数（形状）二、广播机制如果用了axis之后，那个被求和的维度就没有了。但是想利

Pytorch使用教学9-张量的线性代数运算

Antai_ZHU的博客

07-25

1284

在机器学习建模过程中，经常会使用矩阵运算以提升效率，在深度学习中，往往会涉及矩阵的集合运算，就是三维或四维数据的计算。？本文首先介绍矩阵的构造，然后详解矩阵的运算与本质意义。

pytorch_lesson4 张量的线性代数运算(矩阵的形变及特殊矩阵构造方法+矩阵的基本运算+矩阵的线性代数运算+矩阵的分解)

weixin_51589123的博客

05-09

2108

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、pandas是什么？二、使用步骤1.引入库2.读入数据总结前言提示：这里可以添加本文要记录的大概内容：例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。提示：以下是本篇文章正文内容，下面案例可供参考一、pandas是什么？示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。二、使用步骤 1.引入库代.

EP04：【DL】张量的线性代数运算

最新发布

CH3_CH2_CHO的博客

08-07

1395

本文介绍了BLAS和LAPACK作为现代科学计算的核心基础设施，重点阐述了矩阵的基本操作与运算。首先概述了BLAS的三级运算体系和LAPACK的高级功能，它们在深度学习框架中的关键支撑作用。接着详细讲解了矩阵形变（转置）和特殊矩阵构造（单位矩阵、对角矩阵、三角矩阵）的原理与应用场景，通过PyTorch代码示例展示了具体实现方法。最后介绍了矩阵基本运算（点积、矩阵乘法等）及其工程意义，强调这些运算是构建复杂模型的基础模块。全文突出了线性代数运算在实际问题中的高效实现和广泛用途。

pytorch学习09：矩阵基本运算

HMT的博客

08-03

999

四则运算 import torch a = torch.tensor([ [1,2], [3,4] ]) b = torch.tensor([ [10, 20] ]) # 加 print("torch.all(torch.eq(a+b, torch.add(a,b))):", torch.all(torch.eq(a+b, torch.add(a,b)))) print("a+b:\n{}\n".format(a+b)) # 减 print("torch.all(

pytorch_sparse:优化的Autograd稀疏矩阵运算的PyTorch扩展库

05-10

PyTorch稀疏该软件包包括一个小型扩展库，该库具有自动分级支持，可优化稀疏矩阵运算。该软件包当前包含以下方法：所有包含的操作都适用于不同的数据类型，并且都针对CPU和GPU实施。为了避免创建，此程序包仅通过将index和value张量作为参数传递（对稀疏张量的操作。请注意，autograd支持仅包含value ，因为index是离散的，因此不可微分。安装二进制文件我们为所有主要的OS / PyTorch / CUDA组合提供了点胶轮，请参见。 PyTorch 1.8.0 要安装PyTorch 1.8.0的二进制文件，只需运行 pip install torch-scatter torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+${CUDA}.html 其中${CUDA}应该由cpu ， cu

【无标题】python和Pytorch中的矩阵乘法运算总结

tanhongweibest的博客

12-14

1914

python 和Pytorch的矩阵乘法运算总结

pytorch矩阵计算

chy0315的博客

04-15

1253

class Vector(object): CANNOT_NORMALIZE_ZERO_VECTOR_MSG = 'Cannot normalize the zero vector' def __init__(self, coordinates): self.coordinates = coordinates self.num_samples = len(coordinates) self.dimension = len(coordinate.

PyTorch实战（1）：矩阵运算

zhu_886936的博客

04-22

5874

常见的矩阵运算：基于pytorch和numpy实现 import torch import numpy as np import torch.nn as nn X = torch.rand(4, 2, 3) linear = nn.Linear(3, 2) """矩阵加法""" # Z=W+X W = torch.randn(4, 2, 3) Z11 = W + X print(Z11)...

torch进行矩阵运算

m0_46702604的博客

12-23

2876

用torch进行矩阵运算下面我主要区别以下几个函数： torch.mul(a,b) torch.matmul(a,b) torch.mm(a,b) torch.einsum(a,b) 其中，torch.mm()、torch.matmul()、torch.mul() 是我们比较常用的，但是用torch.einsum() 可以实现上述三个函数的任何一个的功能，下面我一一介绍这些函数的用法和适用情况。 torch.mul(a,b) 这个函数就是实现两个张量之间元素对元素的运算，也就是

torch的矩阵运算笔记

weixin_50727642的博客

06-01

719

torch的矩阵运算

torch矩阵计算

Dwendwen_Liu的博客

01-08

680

无

Python实现矩阵秩的算法

BUG？不存在的！

05-23

733

该函数接收一个numpy数组作为输入参数，输出矩阵的秩。实际上，它采用了高斯消元法的技术，将矩阵转化为行简化阶梯形式，从而计算矩阵的秩。矩阵是线性代数中非常重要的概念，其秩是矩阵的核心指标之一。在Python中，我们可以通过简单的代码来实现矩阵的秩的计算。在本例中，输入矩阵的秩为2。在这里，我们调用了rank_of_matrix函数，该函数接收上述矩阵作为输入并输出其秩。通过这个简单的Python算法，我们可以轻松地计算矩阵的秩。如果你对线性代数感兴趣，那么这将是一个很好的起点。

torch使用踩坑日记，矩阵加速运算

weixin_43918046的博客

03-08

2425

我们知道矩阵运算可以加速，用torch搭建的模型，我们预测数据往往都是同时读取多条（在显卡支持的条件下尽可能同时处理多条数据），这样时间会很快，如果单条数据预测非常慢的，最近在写模型处理大数据，我加载多条数据一起处理，因为数据量太大，没法直接全部转换成矩阵，所以是用列表储存了数据，然后预测的时间就是切片导入到模型中，如下代码所示。 import torch from torch.autograd import Variable from torch import nn import numpy as np

PyTorch中文文档精华：张量操作与核心功能速览

`torch.eye`会生成一个二维张量，其主对角线上的元素为1，其余位置的元素为0。这个函数在初始化权重矩阵或构建基础数学结构时非常实用。这只是PyTorch中文文档的一部分，实际上文档还涵盖了张量的索引、切片、拼接...