数据结构6-线索二叉树_第6关:线索二叉树-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_44177768/article/details/127575071

1.补空法创建二叉树

输入一串节点信息 ---》转换 ------》二叉树

前序遍历：ABD##E##CF#G### -----》反过来应用

(1)输入一个补空后的二叉树 ----》先序遍历 ABD##E##CF#G###

(2)转换 char ch ;
ch == '#' ; ------> 空二叉树
ch != '#' ; -------> 创建一个新节点 ---》左子树右子树
又是递归思想

代码：

#include <stdio.h>
#include <stdlib.h>
 
// 二叉树节点
struct BinTree_node
{
        unsigned char elem;     // 二叉树内容
        struct BinTree_node *ltree, *rtree;    //左右树
}; 
 
// 声明

void pre_order(struct BinTree_node *tree);
void in_order(struct BinTree_node *tree);
void pos_order(struct BinTree_node *tree);

struct BinTree_node *create_bintree(void);   //ask_method创建二叉树
struct BinTree_node *Create_BinTree(void);   //fill_blank_method创建二叉树
// 主函数
int main(void)
{      
	struct BinTree_node *mytree;
        printf("please input a preorder binary tree(with fill blank #):\n");
	mytree = Create_BinTree();
        pre_order(mytree);
        printf("\n");
        in_order(mytree);
        printf("\n");
        pos_order(mytree);
        printf("\n");
	return 0;
}
 
//ask_method创建二叉树
struct BinTree_node *create_bintree(void)  
{
	unsigned char flag;
	struct BinTree_node *tree;
 
        tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	printf("please input the mode elem:\n");
	while((tree->elem = getchar()) == '\n');
    //左子树
	printf("do you want to insert l_tree for %c, (Y/N)?\n", tree->elem);
	while((flag = getchar()) == '\n');     //避免连续getchar(),该方法避免回车
        if(flag == 'Y')
		tree->ltree = create_bintree();  //递归创建左子树
        else
		tree->ltree = NULL;
    //右子树
	printf("do you want to insert r_tree for %c, (Y/N)?\n", tree->elem);
        while((flag = getchar()) == '\n');     //避免连续getc har(),该方法避免回车
        if(flag == 'Y')
               tree->rtree = create_bintree();  //递归创建左子树
        else
               tree->rtree = NULL;
        return tree;
}

//fill_blank_method创建二叉树
struct BinTree_node *Create_BinTree(void) 
{
       char ch;
       struct BinTree_node *tree;  
       scanf("%c", &ch);    //获取ch
       if(ch == '#')
            tree = NULL;
       else 
       {
            tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
            tree->elem = ch;
            tree->ltree = Create_BinTree();
            tree->rtree = Create_BinTree();
       }
       return tree;
       
} 



// 先序遍历函数  ABDECFG
 
void pre_order(struct BinTree_node *tree)
{
     if(tree)
     {
          printf("%c", tree->elem);
          pre_order(tree->ltree);
          pre_order(tree->rtree);
     }
}
 
// 中序遍历函数   DBEAFGC
 
void in_order(struct BinTree_node *tree)
{
     if(tree)
     {
          in_order(tree->ltree);
          printf("%c", tree->elem);
          in_order(tree->rtree);
     }
}
 
// 后序遍历函数  DEBGFCA
void pos_order(struct BinTree_node *tree)
{
     if(tree)
     {
          pos_order(tree->ltree);
          pos_order(tree->rtree);
          printf("%c", tree->elem);
     }
}

结果：

2.线索二叉树

传统二叉树：非线性结构（通过指针联系起来）

二叉树 ------》线索化（为了快速找到前驱和后继）----》中序线索化最好

线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继的信息只有在遍历该二叉树的时候才能得到，所以线索化的过程就是在遍历的过程中修改空指针的过程

中序线索化一个二叉树

中序遍历 ---》DBEAFGC ，如果使用栈或队列消耗内存，更加麻烦
n个节点 ---》2n个指针域，但很多没被利用，如下图14个指针域，但仅仅用了6个，所以我们可以利用起来。如果没有左子树那就指向前驱点，没有右子树就指向后继点。

创建线索二叉树+遍历线索二叉树+搜索线索二叉树前驱后继

#include <stdio.h>
#include <stdlib.h>
 

// 二叉树节点
struct BinTree_node
{
        unsigned char elem;                    // 二叉树内容
        struct BinTree_node *ltree, *rtree;    // 左右树
        int lflag, rflag;                      // 标志位
}; 
 

struct BinTree_node *pre = NULL;
// 声明

void pre_order(struct BinTree_node *tree);
void in_order(struct BinTree_node *tree);
void pos_order(struct BinTree_node *tree);

struct BinTree_node *create_bintree(void);          // ask_method创建二叉树
struct BinTree_node *Create_BinTree(void);          // fill_blank_method创建二叉树
void In_order_Thread(struct BinTree_node *tree);    // 中序线索化二叉树
void Create_Inorder_Thread(struct BinTree_node *T); // 线索化
void Traverse_Inorder_Thred(struct BinTree_node *tree); // 遍历线索化二叉树
struct BinTree_node *Search_Inorder_Thread(struct BinTree_node *tree, char ch);// 搜索二叉树点(和遍历的思想一样)
struct BinTree_node *Prenode_Inorder_Thread(const struct BinTree_node *node); // 找前驱
struct BinTree_node *Succnode_Inorder_Thread(struct BinTree_node *node);      // 找后继

// 主函数
int main(void)
{      
	struct BinTree_node *mytree;
        char ch;
        struct BinTree_node *node, *precursor, *succeed;

        printf("please input a preorder binary tree(with fill blank #):\n");
	mytree = Create_BinTree();       // 创建二叉树
        pre_order(mytree);               // 前序遍历
        printf("\n");
           
        Create_Inorder_Thread(mytree);   // 线索化
         
        printf("traverse inorder_thred tree:");  // 遍历线索化二叉树
        Traverse_Inorder_Thred(mytree);
        printf("\n");
        // 找到该结点
        printf("please enter the node that you want to find it's pre & succ node:\n");
        while((ch = getchar()) == '\n');                               // 避免捕获回车
        node = Search_Inorder_Thread(mytree, ch);
        // printf("node = %c\n", node->elem); 调试是否能找到A
        // 找到该节点的前驱点
        precursor =  Prenode_Inorder_Thread(node);
        if(precursor == NULL)  // 无前驱点
                  printf("node %c has no precursor\n", node->elem);
        else
                  printf("precursor node = %c\n", precursor->elem);

        // 找到该节点的后继点
        succeed =  Succnode_Inorder_Thread(node);
        if(succeed == NULL)  // 无后继点
                  printf("node %c has no succeed node\n", node->elem);
        else
                  printf("succeed node = %c\n", succeed->elem);
	return 0;
}
 
// ask_method创建二叉树
struct BinTree_node *create_bintree(void)  
{
	unsigned char flag;
	struct BinTree_node *tree;
 
        tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	printf("please input the mode elem:\n");
	while((tree->elem = getchar()) == '\n');
        // 左子树
	printf("do you want to insert l_tree for %c, (Y/N)?\n", tree->elem);
	while((flag = getchar()) == '\n');       // 避免连续getchar(),该方法避免回车
        if(flag == 'Y')
		tree->ltree = create_bintree();  // 递归创建左子树
        else
		tree->ltree = NULL;
        // 右子树
	printf("do you want to insert r_tree for %c, (Y/N)?\n", tree->elem);
        while((flag = getchar()) == '\n');      // 避免连续getc har(),该方法避免回车
        if(flag == 'Y')
               tree->rtree = create_bintree();  // 递归创建左子树
        else
               tree->rtree = NULL;
        return tree;
}

// fill_blank_method创建二叉树
struct BinTree_node *Create_BinTree(void) 
{
       char ch;
       struct BinTree_node *tree;  
       scanf("%c", &ch);    // 获取ch
       if(ch == '#')
            tree = NULL;
       else 
       {
            tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
            tree->elem = ch;
            tree->ltree = Create_BinTree();
            tree->rtree = Create_BinTree();
       }
       return tree;
       
} 


// 先序遍历函数  ABDECFG
 
void pre_order(struct BinTree_node *tree)
{
     if(tree)
     {
          printf("%c", tree->elem);
          pre_order(tree->ltree);
          pre_order(tree->rtree);
     }
}
 
// 中序遍历函数   DBEAFGC
 
void in_order(struct BinTree_node *tree)
{
     if(tree)
     {
          in_order(tree->ltree);
          printf("%c", tree->elem);
          in_order(tree->rtree);
     }
}
 
// 后序遍历函数  DEBGFCA
void pos_order(struct BinTree_node *tree)
{
     if(tree)
     {
          pos_order(tree->ltree);
          pos_order(tree->rtree);
          printf("%c", tree->elem);
     }
}

// 中序线索化
void In_order_Thread(struct BinTree_node *tree)
{
     if(tree)
     {
           //1.对左子树进行中序线索化
           In_order_Thread(tree->ltree);
           //2.处理当前节点
           if(!tree->ltree)
           {
               tree->lflag = 1;
               tree->ltree = pre;     // 让当前节点左指针指针域指向前驱点
           }
           else
               tree->lflag = 0;
                      
           if(pre)
           {
               if(!pre->rtree)
               {
                    pre->rflag = 1;
                    pre->rtree = tree;     // 让前驱点的右子树指向现在的点
               }
               else
                    pre->rflag = 0;
           }
           pre = tree;                // 更新前驱点 
           //3.对右子树进行中序线索化
           In_order_Thread(tree->rtree);
     }
}


// 线索化打包
void Create_Inorder_Thread(struct BinTree_node *T)
{ 
        if(T)
        {
             In_order_Thread(T);
             pre->rtree = NULL;
             pre->rflag = 1;
        }
}

// 遍历线索化二叉树（不能用原来的遍历）
void Traverse_Inorder_Thred(struct BinTree_node *tree)
{
      
       while(tree)
       {
               // 使用循环找到最左下角的节点
               while(tree->lflag == 0)
               {
                      tree = tree->ltree;
               }
               printf("%c ", tree->elem);  
               // 该节点如果存在后继节点并且确实存在内容   tree-> B
               while((tree->rflag == 1) && (tree->rtree))  
               {
                      tree = tree->rtree;
                      printf("%c ", tree->elem);
               }
               // 如果该结点存在rtree ,后继节点应该是该结点右子树最左下的节点,再次循环    
              tree = tree->rtree;  
       }
}

// 搜索二叉树点(和遍历的思想一样)
struct BinTree_node *Search_Inorder_Thread(struct BinTree_node *tree, char ch)
{ 
      while(tree)
      {
               // 使用循环找到最左下角的节点
               while(tree->lflag == 0)              
                      tree = tree->ltree;          
               if(tree->elem == ch)
                      return tree; 
               // 该节点如果存在后继节点并且确实存在内容   tree-> B
               while((tree->rflag == 1) && (tree->rtree))  
               {
                      tree = tree->rtree;
                      if(tree->elem == ch)
                            return tree; 
               }
               // 如果该结点存在rtree ,后继节点应该是该结点右子树最左下的节点,再次循环    
              tree = tree->rtree;  
      }    
}

// 找前驱点
struct BinTree_node *Prenode_Inorder_Thread(const struct BinTree_node *node)
{
       struct BinTree_node *nd;
       // 无左子树，有前驱点
       if(node->lflag == 1)   
             return node->ltree;
       // 有左子树，找左子树最右下的点
       else               
       {
             nd = node->ltree;
             while(nd->rflag == 0)
                  nd = nd->rtree; 
             return nd;          // 找到最右下的节点
       }
              
}

// 找后继点
struct BinTree_node *Succnode_Inorder_Thread(struct BinTree_node *node)
{
       struct BinTree_node *nd;
       // 无右子树，有后继点
       if(node->rflag == 1)   
             return node->rtree;
       // 有右子树，找右子树最左下的点
       else               
       {
             nd = node->rtree;
             while(nd->lflag == 0)
                  nd = nd->ltree; 
             return nd;          // 找到最左下的节点
       }
}

3.还原遍历二叉树

根据二叉树的已知遍历还原二叉树

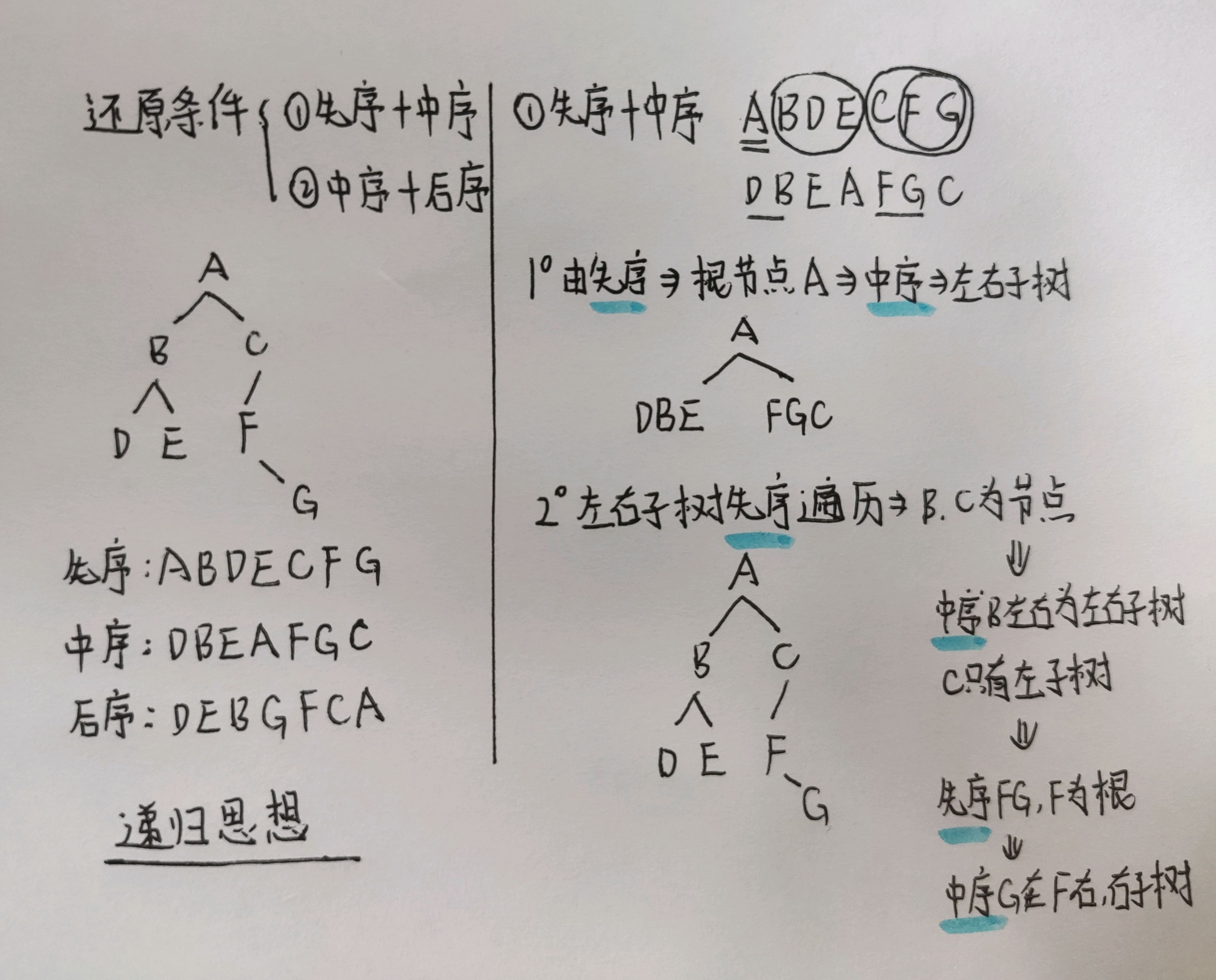
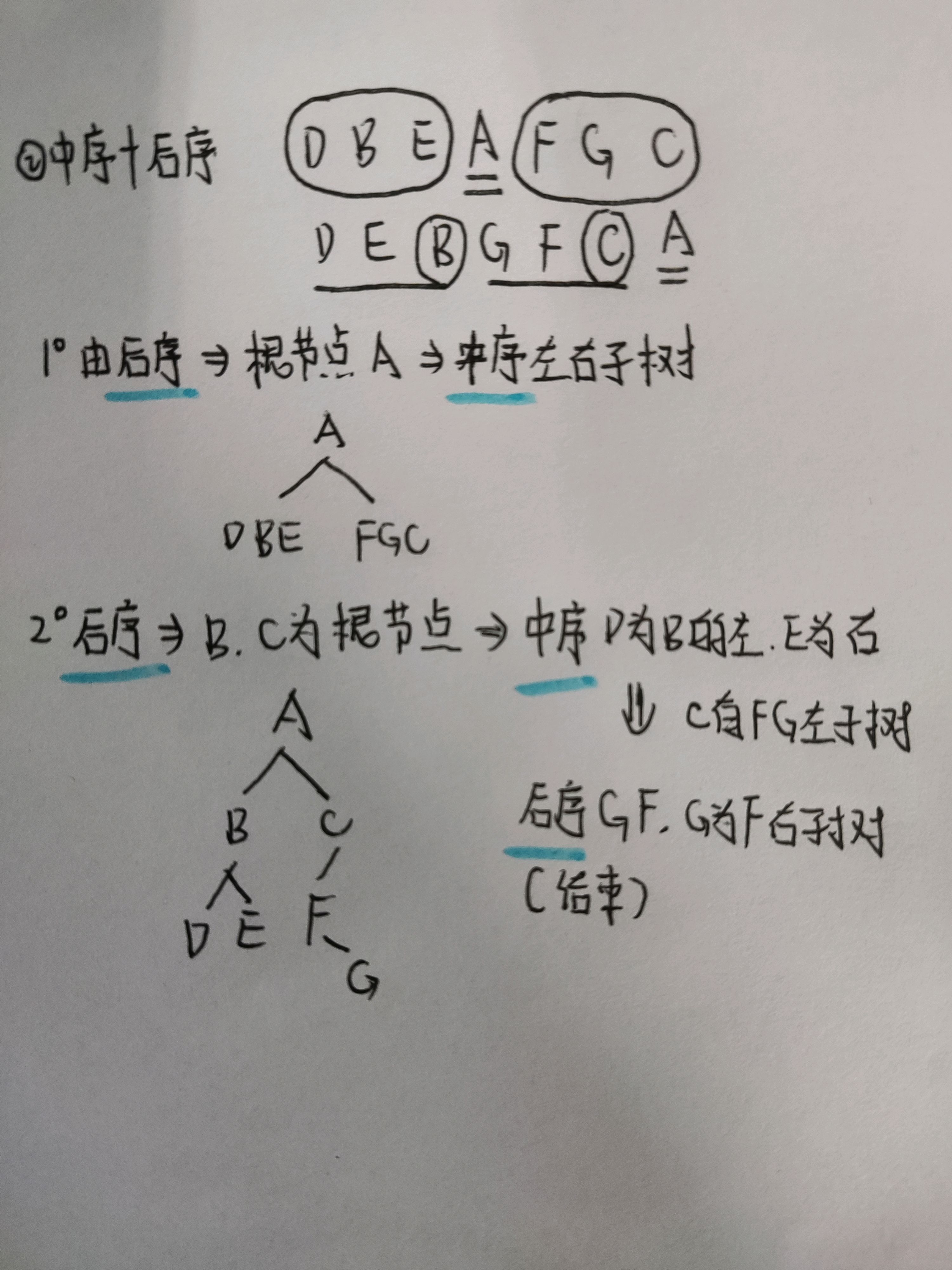
revert_bintree.c

#include <stdio.h>
#include <stdlib.h>
 
// 二叉树节点
struct BinTree_node
{
        unsigned char elem;                    // 二叉树内容
        struct BinTree_node *ltree, *rtree;    // 左右树
}; 
 
// 声明

void pre_order(struct BinTree_node *tree);
void in_order(struct BinTree_node *tree);
void pos_order(struct BinTree_node *tree);

struct BinTree_node *create_bintree(void);   //ask_method创建二叉树
struct BinTree_node *Create_BinTree(void);   //fill_blank_method创建二叉树
struct BinTree_node *pre_in_CreatBinTree(char *pre, char *in, int len); // 先序+中序还原二叉树 
struct BinTree_node *in_post_CreatBinTree(char *in, char *post, int len);
// 主函数
int main(void)
{      
	struct BinTree_node *mytree;

        char pre[100], in[100], post[100];
        int choose, n;
        printf("1. revert binarytree through pre & in order:\n");
        printf("2. revert binarytree through post & in order:\n");
        scanf("%d", &choose);
        switch(choose)
        {
            case 1:
                   printf("please enter the number of nodes:");
                   scanf("%d", &n);
                   getchar();  //消耗掉回车
                   printf("please enter the pre order:");
                   gets(pre);
                   printf("please enter the in order:");
                   gets(in);
                   mytree = pre_in_CreatBinTree(pre, in, n);
                   printf("after revert, show the bintree in post order:");
                   pos_order(mytree);
                   printf("\n");
                   break;
            case 2:
                   printf("please enter the number of nodes:");
                   scanf("%d", &n);
                   getchar();  //消耗掉回车
                   printf("please enter the in order:");
                   gets(in);
                   printf("please enter the pos order:");
                   gets(post);
                   mytree = in_post_CreatBinTree(in, post, n);
                   printf("after revert, show the bintree in pre order:");
                   pre_order(mytree);
                   printf("\n");
                   break;
        }
        printf("\n");
	return 0;
}
 
//ask_method创建二叉树
struct BinTree_node *create_bintree(void)  
{
	unsigned char flag;
	struct BinTree_node *tree;
 
        tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	printf("please input the mode elem:\n");
	while((tree->elem = getchar()) == '\n');
    //左子树
	printf("do you want to insert l_tree for %c, (Y/N)?\n", tree->elem);
	while((flag = getchar()) == '\n');     //避免连续getchar(),该方法避免回车
        if(flag == 'Y')
		tree->ltree = create_bintree();  //递归创建左子树
        else
		tree->ltree = NULL;
    //右子树
	printf("do you want to insert r_tree for %c, (Y/N)?\n", tree->elem);
        while((flag = getchar()) == '\n');     //避免连续getc har(),该方法避免回车
        if(flag == 'Y')
               tree->rtree = create_bintree();  //递归创建左子树
        else
               tree->rtree = NULL;
        return tree;
}

//fill_blank_method创建二叉树
struct BinTree_node *Create_BinTree(void) 
{
       char ch;
       struct BinTree_node *tree;  
       scanf("%c", &ch);    //获取ch
       if(ch == '#')
            tree = NULL;
       else 
       {
            tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
            tree->elem = ch;
            tree->ltree = Create_BinTree();
            tree->rtree = Create_BinTree();
       }
       return tree;
       
} 



// 先序遍历函数  ABDECFG
 
void pre_order(struct BinTree_node *tree)
{
     if(tree)
     {
          printf("%c", tree->elem);
          pre_order(tree->ltree);
          pre_order(tree->rtree);
     }
}
 
// 中序遍历函数   DBEAFGC
 
void in_order(struct BinTree_node *tree)
{
     if(tree)
     {
          in_order(tree->ltree);
          printf("%c", tree->elem);
          in_order(tree->rtree);
     }
}
 
// 后序遍历函数  DEBGFCA
void pos_order(struct BinTree_node *tree)
{
     if(tree)
     {
          pos_order(tree->ltree);
          pos_order(tree->rtree);
          printf("%c", tree->elem);
     }
}

// 用先序+中序还原二叉树
struct BinTree_node *pre_in_CreatBinTree(char *pre, char *in, int len)
{
      struct BinTree_node *tree;
      if(len == 0)              // 长度为0，结束循环
             return NULL;
      char ch = pre[0];
      int index = 0;
      while(in[index] != ch)
            index++;

      tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
      tree->elem = ch;
      tree->ltree = pre_in_CreatBinTree(pre+1, in, index);  // 左子树
      tree->rtree = pre_in_CreatBinTree(pre+index+1, in+index+1, len-index-1);  // 右子树
      
      return tree;
}

// 用后序+中序还原二叉树
struct BinTree_node *in_post_CreatBinTree(char *in, char *post, int len)
{
      struct BinTree_node *tree;
      if(len == 0)              // 长度为0，结束循环
             return NULL;
      char ch = post[len-1];    // 后序最后一个为根结点
      int index = 0;
      while(in[index] != ch)    // 找到中序根结点
           index++;

      tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
      tree->elem = ch;
      tree->ltree = in_post_CreatBinTree(in, post, index);                     // 左子树
      tree->rtree = in_post_CreatBinTree(in+index+1, post+index, len-index-1);  // 右子树
      
      return tree;
}

结果