数据挖掘week5

                              支持向量机

1. 什么是SVM，SVM产生的意义
   1.1什么是SVM？
   SVM(Support Vector Machine)译为支持向量机，又名最大间隔分类器。它不是一种机器，而是一种机器学习算法。它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。
   支持向量机方法是建立在统计学理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的泛化能力。
   1.2SVM产生的意义
   SVM在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。
   1）小样本，指的是与问题的复杂度相比，SVM要求的样本数相对较少；
   2）非线性，指的是SVM擅长应付样本数据线性不可分的情况，主要通过核函数和松弛变量来实现，这一块是SVM的精髓；
   3）高维，指的是样本维数很高，因为SVM产生的分类器很简洁，但算法用到的样本信息很少，仅仅用到支持向量。
   4）由于分类器仅由支持向量决定，SVM还能够有效避免过拟合。
2. 大间距分类的含义
   支持向量机也叫做大间距分类器，最本质的含义就是最显著的划分不同类别的数据，如图1所示，假设数据样本集中存在两个类别的数据，这两个类别的数据分隔的足够开，因此很容易就可以在二维图中画出一条直线将两类数据点分开，这组数据被称为线性可分（linearly separable）数据。而最大间距分类负责的事情就是找到距离两组数据最大距离的分界线（三维空间内为分界面），也就是图1中的黑线。这一分界线也称为分隔超平面（separating hyperplane）。其存在的意义在于：数据点离决策边界越远，最后的预测结果也就越可信，模型的鲁棒性也就更强。寻找分隔超平面的方法在于，找到离分隔超平面最近的点，这些点就是支持向量（support vector），接下来最大化支持向量到分隔面的距离，这一过程就被称为大间距分类。
   
3. 核函数
   3.1.线性核函数
   
   

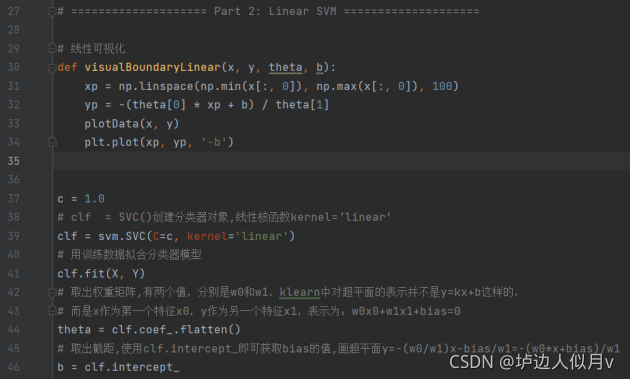
数据集如下图

线性核函数分类效果如下

3.2.高斯核函数（RBF核函数）

高斯核函数代码

数据集如下图所示

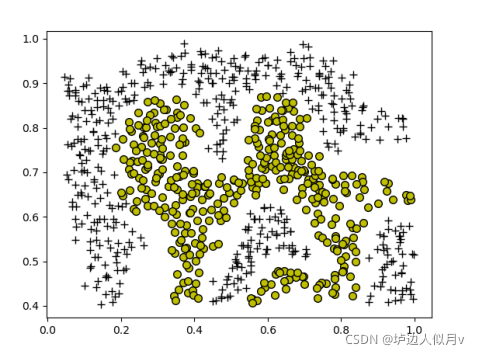
高斯核函数分类结果如下图

3.3.多项式核函数

多项式核函数代码

数据集如下图所示

多项式核函数分类结果如下图