Manacher算法

Manacher算法是求解一个字符串的最长回文串长度的线性做法；如果暴力求解最长回文串，也就是枚举每个回文串的中心，之后向两边拓展的方法， 复杂度达到了O(nn)，而Manacher则将其优化到了O(n);
首先，一个字符串的最长回文串可能有奇数个字符，也可能有偶数个，Manacher算法为了统一，进行了预处理，在每个字符的前面和后面都加上了一个从未在原字符串中出现过的字符，从而使得所有回文串长度都变成了奇数。例如abab经预处理后就成了#a#b#a#b#。
其次，设定一个回文串半径数组p，p[i]代表以i为中心的回文串的长度；

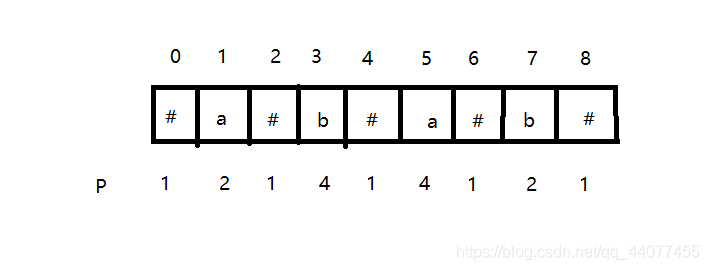
这样通过p数组我们就可以知道以i为中心的原回文串（就是没有添加辅助字符时的回文串）的长度及其起始位置：
1.长度len = p[i] - 1，原因是以i为中心的回文串长度易得为2p[i]-1，而回文串中辅助字符#总比原字符数量多1，所以，辅助字符#有p[i]个，原字符有p[i] - 1个；比如i=3时，p[3] = 4，对应回文串aba长度是3
2.起始位置：先给结论pos = (i-p[i])/2，求取起始位置的时候还需要在起始和末尾添加两个不同的辅助字符，如果不添加，那么因为我们计算回文半径的时候考虑了中心本身，那么最终半径p[i]可能会大于i，从而导致pos为负，为了解决这个问题，需要在添加辅助字符，使得有效下标从1开始；
p数组的求解
可以上看以上都是在已知p数组后才有的结论，所以我们需要求解p数组，求解i时，我们要知道对于所有0<j<=1，j+p[j]的最大值mx，以及对应的j，也就是回文串右端点的最远位置，但是这个位置上的字符不属于以j为中心的回文串。
1.如果i < mx，i也就位于j~mx间，i关于j一定有对称点k = 2 * j- i，且若I+p[k] < mx，p[i] = p[k]；否则p[i]至少是mx - i;并且要继续拓展看是否能形成更长的回文串，也就是p[i] 至少是 min(p[k],mx-i);还需要进行拓展寻找更长的回文串
2.如果i >= mx，那么就只能老实地从i进行中心拓展。
模板题

//#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
const int maxn = 110000 + 50;
const int maxm = 1e4 + 10;
const int inf_max = 0x3f3f3f;
using namespace std;
char str[maxn],a[maxn<<1];
int p[maxn<<1];
int Manacher() {
    int l = 0,len = strlen(str),id,mx;
    a[l++] = '$';
    a[l++] = '#';
    for(int i = 0;i < len; ++i) {
        a[l++] = str[i];
        a[l++] = '#';
    }
    a[l] = 0;
    id = 0,mx = 0;
    for(int i = 0;i < l; ++i) {
        p[i] = (mx > i ? min(p[2 * id - i],mx - i) : 1);
        while(a[i + p[i]] == a[i - p[i]]) p[i]++;
        if(p[i] + i > mx) {
            id = i;
            mx = p[i] + i;
        }
    }
    return l;
}
int main()
{
    while(~scanf("%s",str)) {
        int len = Manacher();
        int ans = 1;
        for(int i = 0;i < len; ++i) {
            ans = max(ans,p[i] - 1);
        }
        cout<<ans<<endl;
    }
    return 0;
}