α − β \alpha-\beta α−β极大极小值剪枝算法
若正常使用搜索算法来穷举所有可能性进行判断,那范围是非常巨大的,就算 3 × 3 3\times3 3×3的井字棋,他第一步就有9种下法,第二步就有 9 × 8 9\times8 9×8种下法,最后一步更是达到 9 ! 9! 9!种下法,更不用说 15 × 15 15\times15 15×15的五子棋。
所以说我们得在搜索的基础上进行剪枝,将一些根本不需要走到的分支抛弃掉,这让就能够大大减少我们的复杂度。
算法原理
首先,明白几个概念:
- 为了便于搜索,我们会对棋局进行打分(比如自己四子连成一线+10,对手四子连成一线-10),分越高,对自己越有利,分越低,对对手越有利
- α \alpha α表示自己可以选择的最小值,而我们搜索的目的就是为了不断提高我们的最小值
- β \beta β表示对手可以选择的最大值,对于对手来说要不断降低它的最大值,这样才对它更有利(参见第一点)。
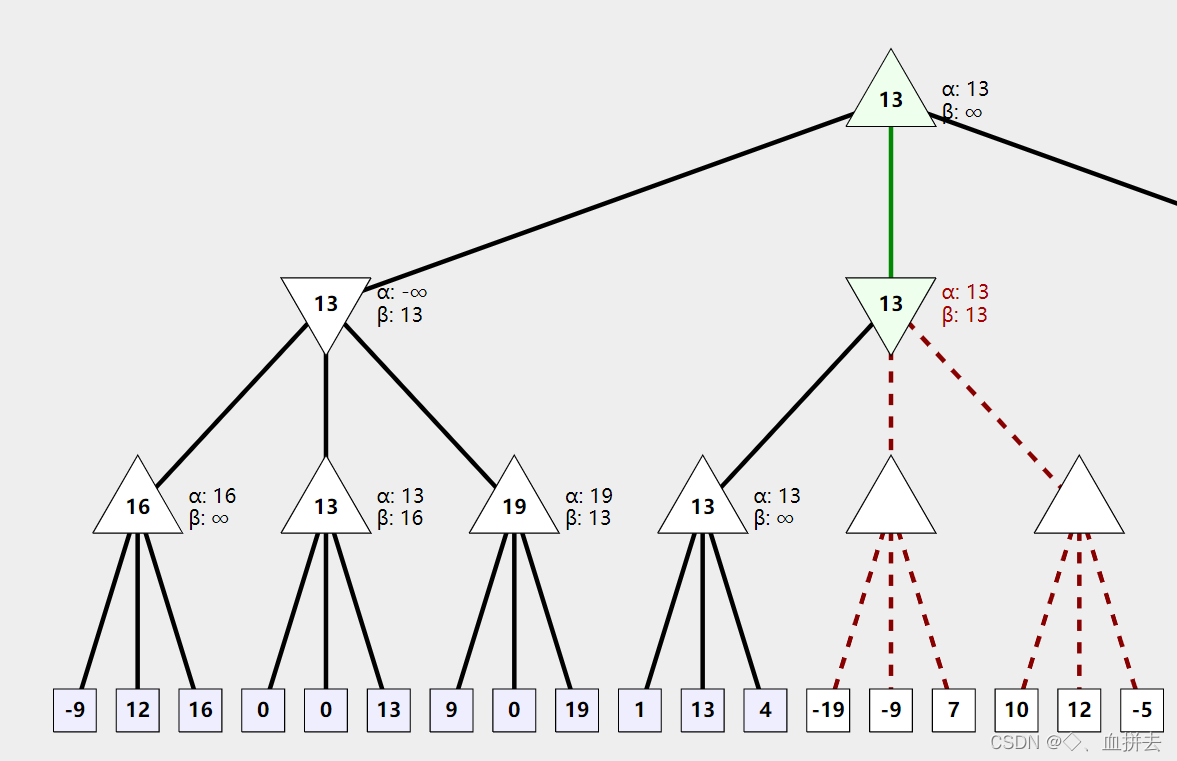
我们假设搜索深度为3,即往后想三步,构造出来的搜索树(局部)如下。
正三角表示自己回合,倒三角表示对手回合,正方形为最终可选的棋局。
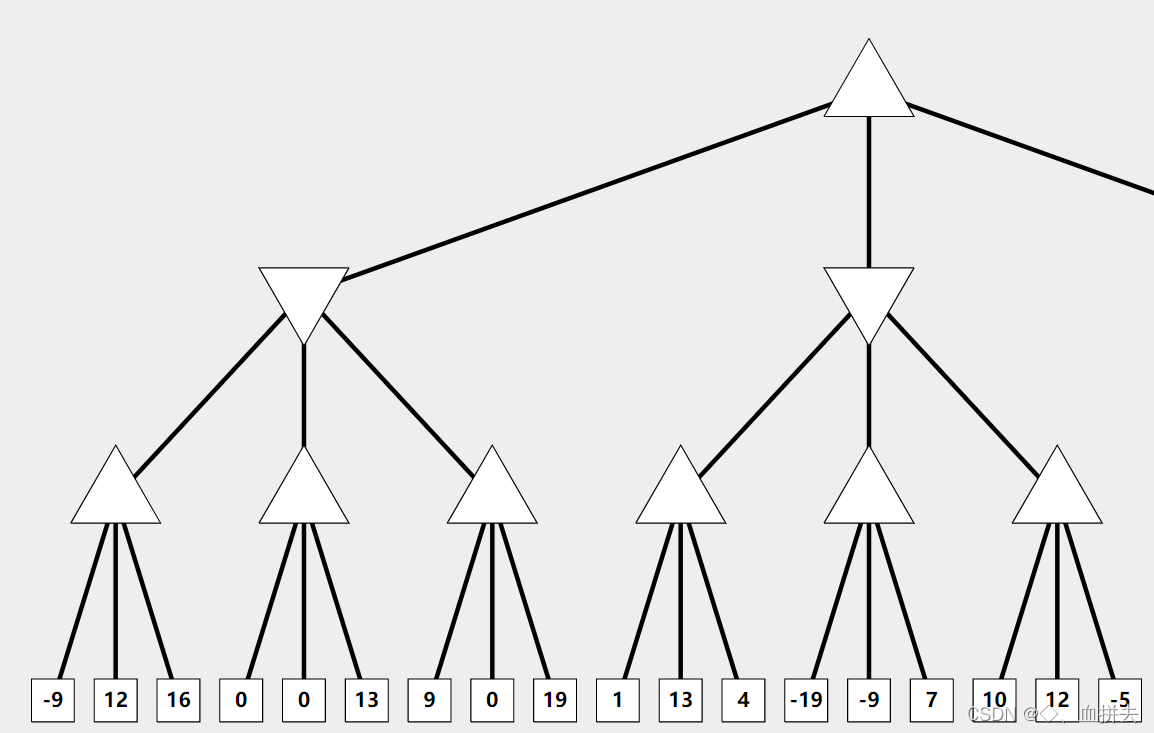
现在只是先把树画出来,还没有开始搜索,开始搜索时,将根节点 [ α , β ] [\alpha,\beta] [α,β]初始化为 [ − ∞ , + ∞ ] [-\infin,+\infin] [−∞,+∞],然后往下搜索,到达的非叶子节点时,也将其初始化同样的值,到达叶节点时,对棋局进行打分,并开始回溯。
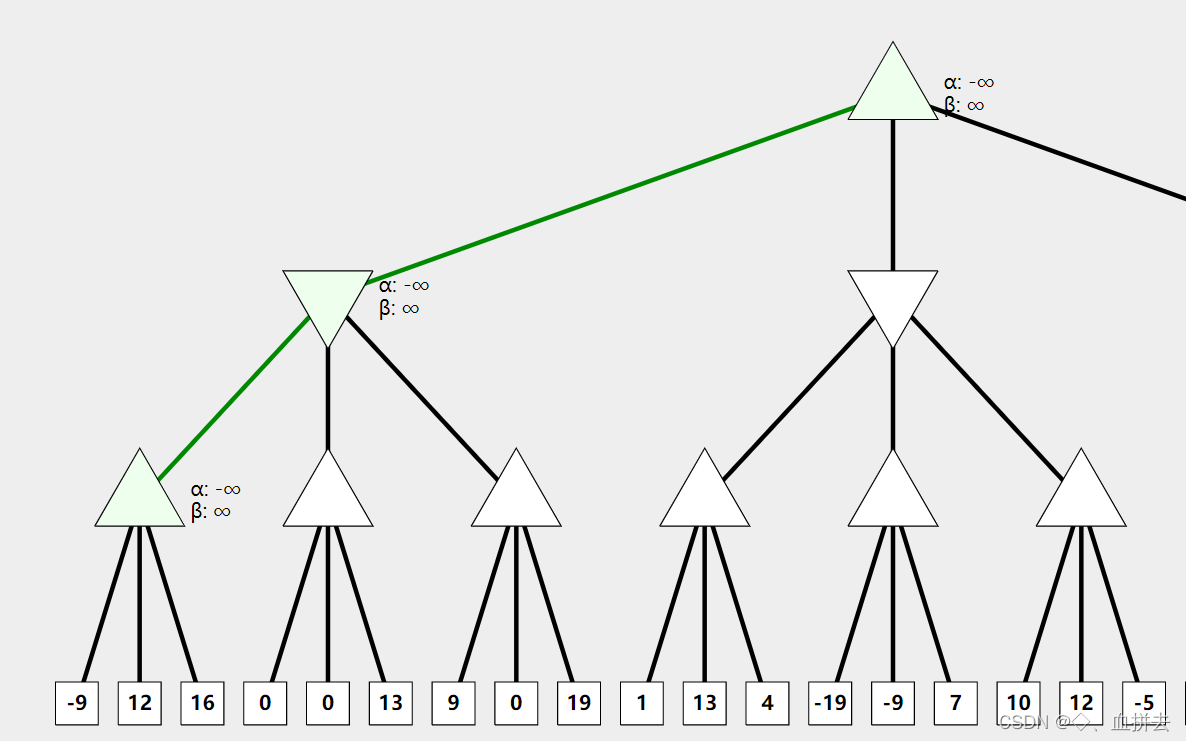
此时,第一个叶子节点为 − 9 -9 −9,此时在自己回合,我们会选择值比较大的棋局,然后与 α \alpha α以及自己当前值进行比较,大于则更新 α \alpha α与自己当前值,再继续搜索其他正方形节点,并不断更新。
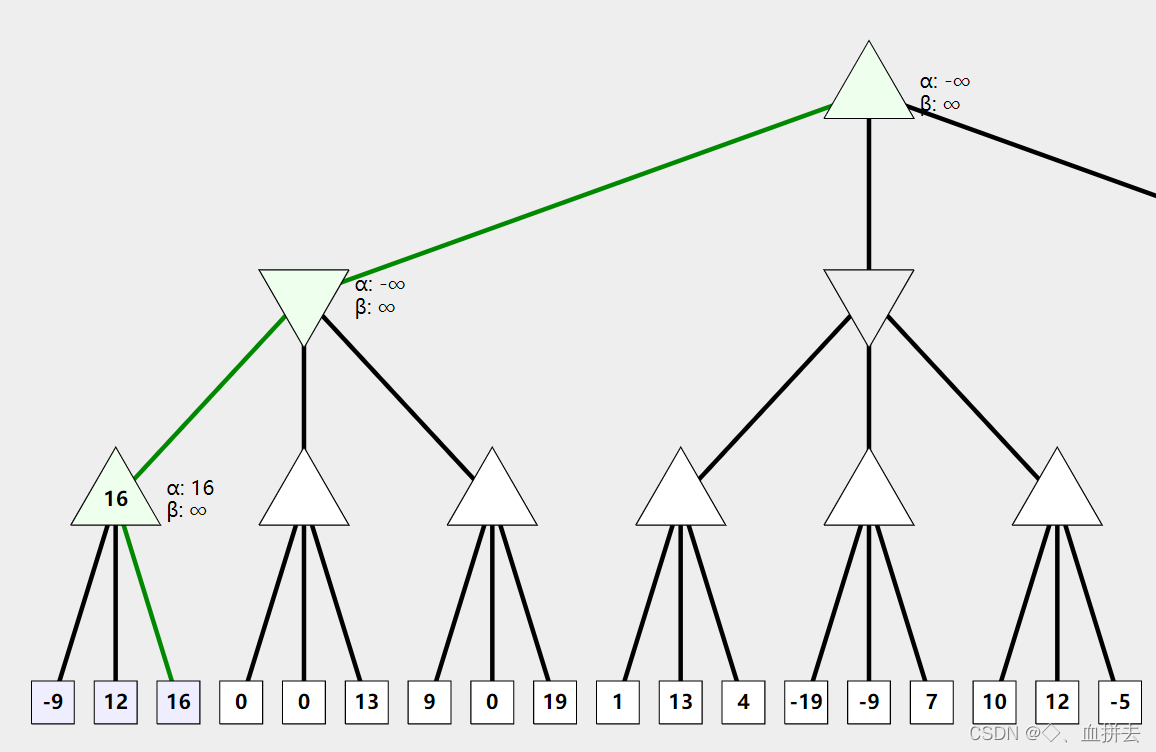
搜索完此节点下所有叶节点后开始回溯,此时正三角形的值更新为16,回溯到上一个节点后,为对手回合,选择较小的值来更新 β \beta β, 16 < + ∞ 16 < +\infin 16<+∞,所以更新值,然后再搜索另一个节点,往下搜索时,会先将更新后的 α , β \alpha,\beta α,β值赋给该节点,其他操作基本同样操作。
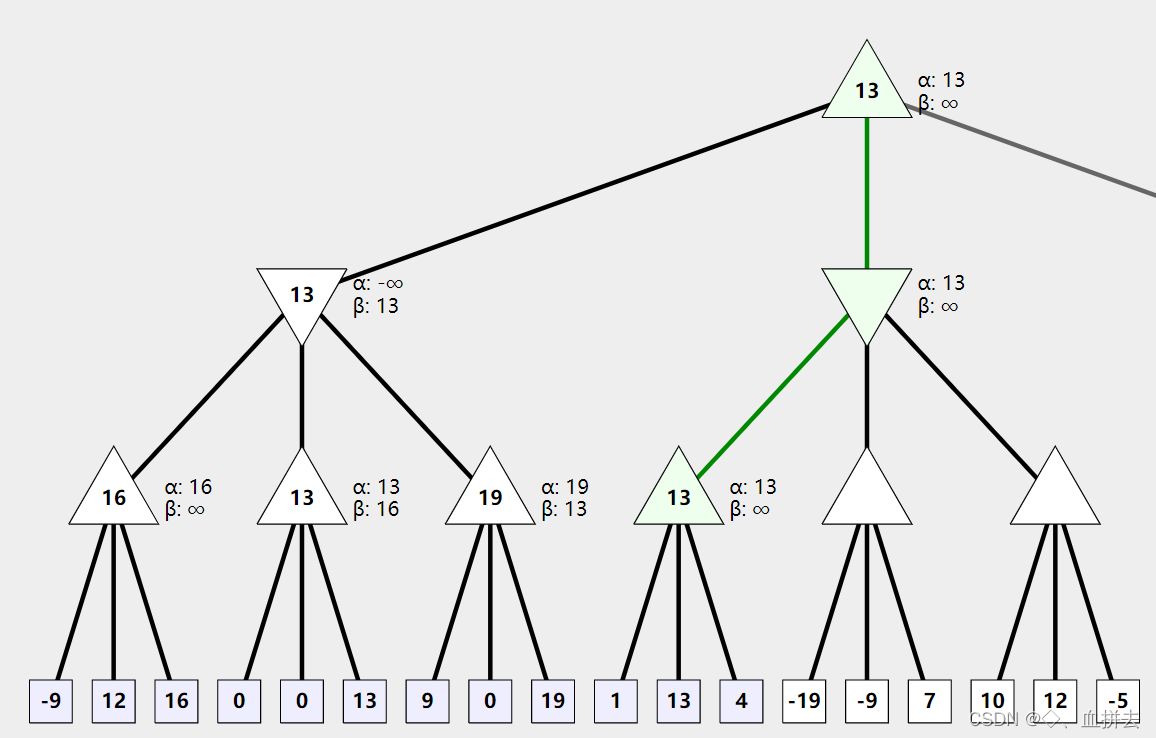
上面我们还只讲到如何更新 α , β \alpha,\beta α,β的值,并未进行剪枝操作,只能说好戏还在后头,此时绿色路径上最后一个非叶节点已经搜索完所有叶子节点并更新,回溯到对手回合,选择较小值,更新 β \beta β为 13 13 13,我们发现此时 α , β \alpha,\beta α,β满足 α ≤ β \alpha \le \beta α≤β,先思考以下问题
- 当前非叶节点的 α \alpha α值是来自根节点,也就是说根节点选择更新时,他会选择比 α \alpha α值更小的来更新吗?显然不会,因为 α \alpha α是自己回合分数的下界,根节点要的是不断提高下界。
- 但是对于绿色路径上的第二个节点来说,是要选择比 β \beta β更小的值来更新,所以此节点的值肯定 ≤ 13 \le 13 ≤13。所以剩下的子节点就不用搜索了,直接剪掉。
最后来一张完整的图,可以直接再推一遍,或者上这个网站Alpha-Beta Pruning Practice 模拟下(要某种工具才能访问)。
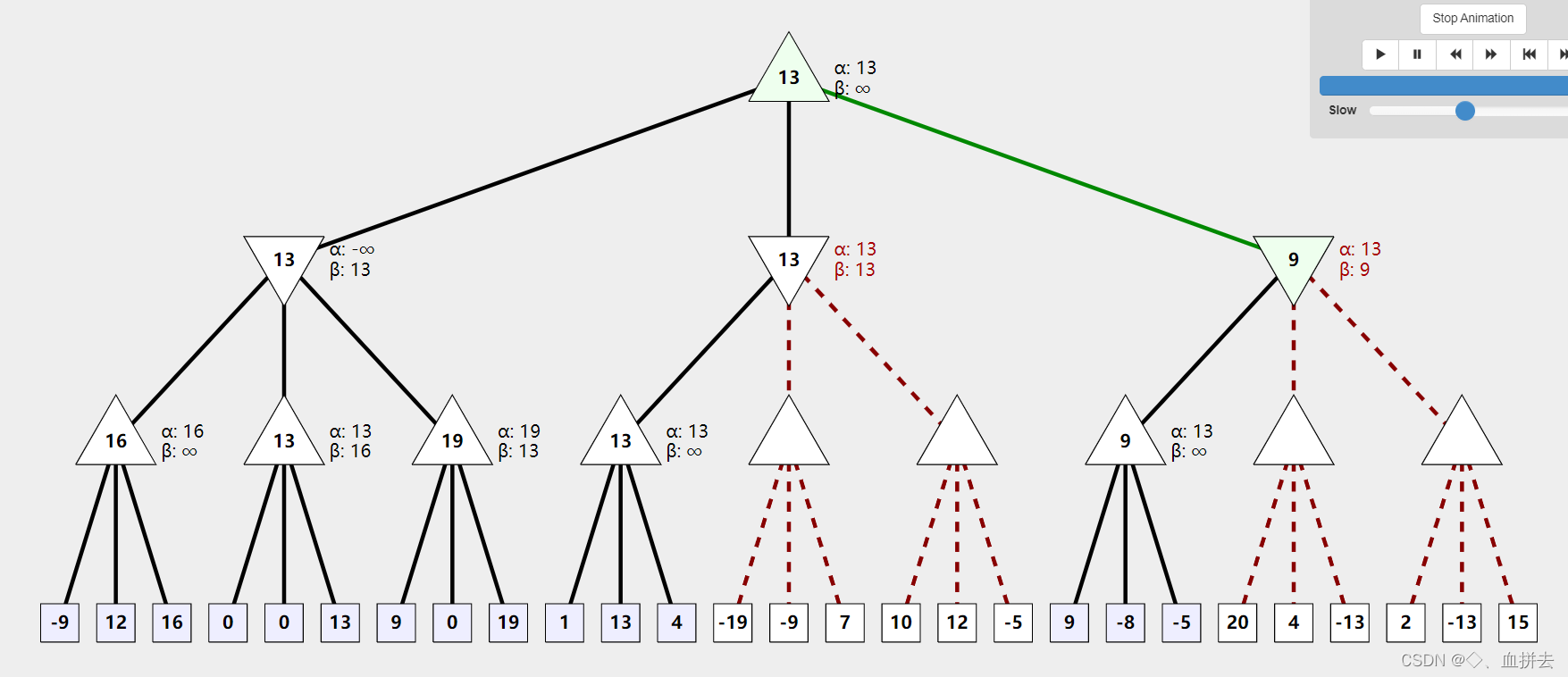





 本文介绍了α-β剪枝算法的基本原理及其在棋类游戏中应用的方法。通过搜索树的构造与剪枝过程,该算法能够有效减少搜索空间,提高搜索效率。
本文介绍了α-β剪枝算法的基本原理及其在棋类游戏中应用的方法。通过搜索树的构造与剪枝过程,该算法能够有效减少搜索空间,提高搜索效率。
















 3076
3076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








