数据结构树及相关算法题

树

定义

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
有一个特殊的结点叫根节点，根节点没有 前驱节点。
除根节点外，其余节点被分为M（M>0）个互不相交的集合T1，T2…Tm，其中每一个集合Ti(1<=i<=m)有是一颗与树类似的子树，每颗子树的根节点有且只有一个前驱，可以有0个或者多个后继。
树是递归定义的。

重要概念

节点的度：一个节点含有的子树的个数称为该节点的度
树的度：一棵树中，最大的节点的度称为树的度
叶子节点或终端节点：度为0的节点称为叶节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点
根结点：一棵树中，没有双亲结点的结点
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
树的高度或深度：树中节点的最大层次
非终端节点或分支节点：度不为0的节点
兄弟节点：具有相同父节点的节点互称为兄弟节点
堂兄弟节点：双亲在同一层的节点互为堂兄弟
节点的祖先：从根到该节点所经分支上的所有节点
子孙：以某节点为根的子树中任一节点都称为该节点的子孙
森林：由m（m>=0）棵互不相交的树的集合称为森林

树的表示形式

树有多种表示方式：双亲表示法、孩子表示法、孩子兄弟表示法等。
孩子兄弟表示法：

class Node{
   
	int value; //树中存储的数据
	Node firstChild;//第一个孩子引用
	Node nextBrother;//下一个兄弟引用
}

二叉树

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点：
每个结点最多有两棵子树，即二叉树不存在度大于 2 的结点
二叉树的子树有左右之分，其子树的次序不能颠倒，因此二叉树是有序树

二叉树的基本形态

从左往右依次是：空树、只有根节点的二叉树、节点只有左子树、节点只有右子树、节点的左右子树均存在，一般二叉树都是由上述基本形态结合而形成的。

满二叉树

满二叉树: 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是$2^k-1$ ，则它就是满二叉树。

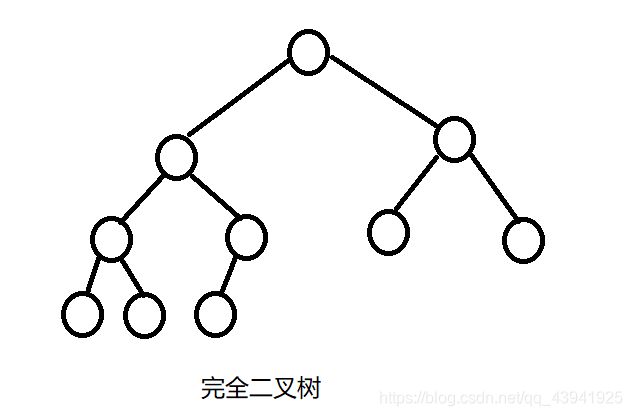
完全二叉树

完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

二叉树的性质

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有$2^{i-1}$(i>0)个结点
若规定只有根节点的二叉树的深度为1，则深度为K的二叉树的最大结点数是$2^k-1$(k>=0)

二叉树的基础面试题

1. 二叉树的前序遍历题目链接
   前中后序的二叉树遍历采用递归的方式来写有一个模板，只需要改变几行代码的顺序就好。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 import java.util.LinkedList;
import java.util.List;
class Solution {
   
    static List<Integer> list = new LinkedList();
    public List<Integer> preorderTraversal(TreeNode root) {
   

        if (root == null){
   
            return new ArrayList<>();
        }
        List<Integer> left = preorderTraversal(root.left);
        List<Integer> right = preorderTraversal(root.right);

        List<Integer> list = new ArrayList<>();
         list.add(root.val);
        list.addAll(left);
        list.addAll(right);
       
        return list;
    }
}

方法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
   

    List<Integer> result;

    public void traversalNode(TreeNode node) {
   
        if(node != null) {
   
            result.add(node.val);
            if(node.left != null) traversalNode(node.left);
            if(node.right != null) traversalNode(node.right);
        }
        return;
    }

    public List<Integer> preorderTraversal(TreeNode root) {
   
        result = new ArrayList<Integer>(); 
        traversalNode(root);
        return result;    
    }
}

3. 二叉树的中序遍历题目链接

class Solution {
   
    public List<Integer> inorderTraversal(TreeNode root) {
   

        if (root == null){
   
            return new ArrayList<>();
        }
        List<Integer> left = inorderTraversal(root.left);
        List<Integer> right = inorderTraversal(root.right);

        List<Integer> list = new ArrayList<>();
        list.addAll(left);
         list.add(root.val);
        list.addAll(right);
       return list;
    }
}

5. 二叉树的后序遍历题目链接

class Solution {
   
    public List<Integer> postorderTraversal(TreeNode root) {
   

       
        if (root == null){
   
            return new ArrayList<>();
        }
        List<Integer> left = postorderTraversal(root.left);
        List<Integer> right = postorderTraversal(root.right);

        List<Integer> list = new ArrayList<>();
        list.addAll(left);
         
        list.addAll(right);
        list.add(root.val);
       return list;
   
    }
}

7. 检查两棵树是否相同题目链接

class Solution {
   
    public boolean isSameTree(TreeNode p, TreeNode q) {
   
        if (p == null && q == null){
   
            return true;
        }else if(p == null || q == null){
   
            return false;
        }else if(p.val != q.val){
   
            return false;
        }else{
   
            return p.val == q.val && isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
        }
        
    }
}

方法二：

 public static boolean isSameTree(TreeNode p, TreeNode q) {
   
        if (p == null && q == null) {
   
            return true;
        }

        if (p == null || q == null