最强学生之KMP，怎么可能看不懂？（数据结构内功修炼之“串”系列）_int bf(string s, string p) { int i=1,j=1; int n = -优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43919400/article/details/116669518

前言：

欢迎大家来到KMP算法的小课堂，如果你只是想知道手算next值和nextval值，那么请往这里走《KMP算法中计算next值和nextval的值》。这里采用教学模式来学习KMP算法，重点是用代码求解KMP和next值、nextval的值，理解其中的原理。当然，本人水平有限，尽力啊！

人物一览：

算法老师：A教授

好学的学生：cat

一、情景一

A教授：现在我们开始上课，假设我们有主串S和子串P，现在谁能告诉我用什么样的方法来检索主串中是否存在子串P，如果存在返回子串在主串中出现的第一个下标，如果不存在返回-1。说着，cat抬头看到黑板上出现了这样的字符：

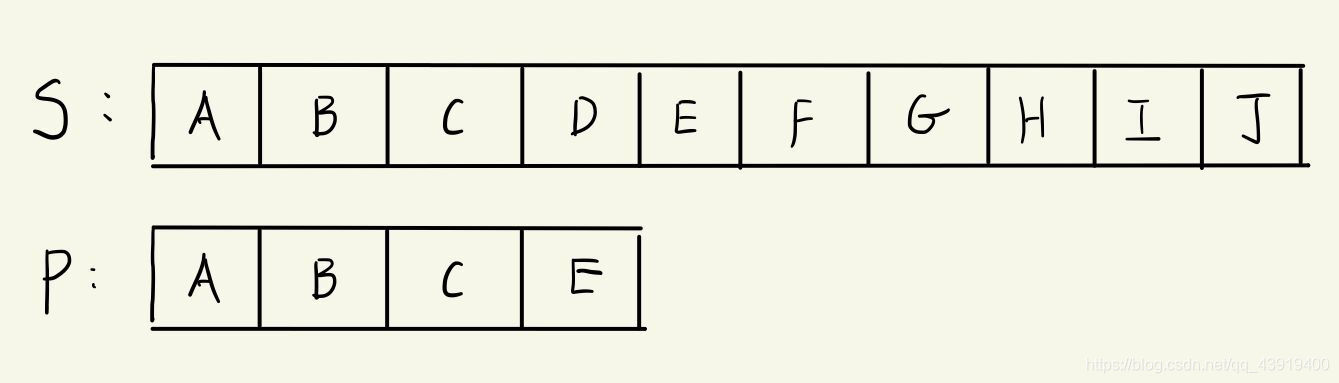
cat思考了一番：“老师，可以直接暴力BF搜索，这里我令S中字符的下标为i，P中字符的下标为j。那么我只需要S、P都从第一个开始比较，如果相等那么就继续往下走，如果i!=j，也就是说出现不匹配的情况的话，就直接j回退到0位置（这里用数组的下标，第一个数组为0），而我们的S退到i-j+1的位置就好”。

A教授：show me your code！

于是cat走到讲台上，开始写下这样的代码：

#include<iostream>
#include<string> 
using namespace std;

int bf(string s,string p) {
	int i = 0;//主串的位置
	int j = 0;//子串的位置
	while(i<s.length()&&j<p.length()) {//子串和主串都没有走完 
		if(s[i]==p[j]) {//匹配 
			i++;
			j++;
		} else{//不匹配
			i = i-j+1;//i后退 
			j = 0;//j归0 
		} 
	}
	if(j==p.length()){
		//子串走完了，匹配成功 
		return i-j;
	} 
	return -1;
}

//测试代码
int main() {
	string s = "ABCDEFGHIJK";
	string p = "ABCE";
	cout<<bf(s,p)<<endl;
	return 0;
}

A教授点了点头，“代码功底很扎实呀cat，但是你有计算过这个算法的时间复杂度吗？”

cat：“老师，这里用暴力递归，我们就看最坏情况下的复杂度吧。假设主串的长度为n，子串的长度为m，最坏的情况就是每一次匹配子串m次然后子串回退到0（也就是说每趟不成功的匹配都发生在模式串的最后一个字符与主串相应字符的比较），例如S="aaaaaab”，P=“aab”。假设我们在主串的第i个位置开始才匹配成功（也就是返回下标为i），那么前面一共比较了i*m次。也就可以看做最坏的时间复杂度为O(n*m)。

A：“时间复杂度不够严谨呀，但你说的对！”。“还有同学有其它的方法吗？”。

二、情景二

老师两眼放光，但全班雅雀无声emmmm

A:“大家不要局限自己的思维，你们看下黑板上的这个例子！”

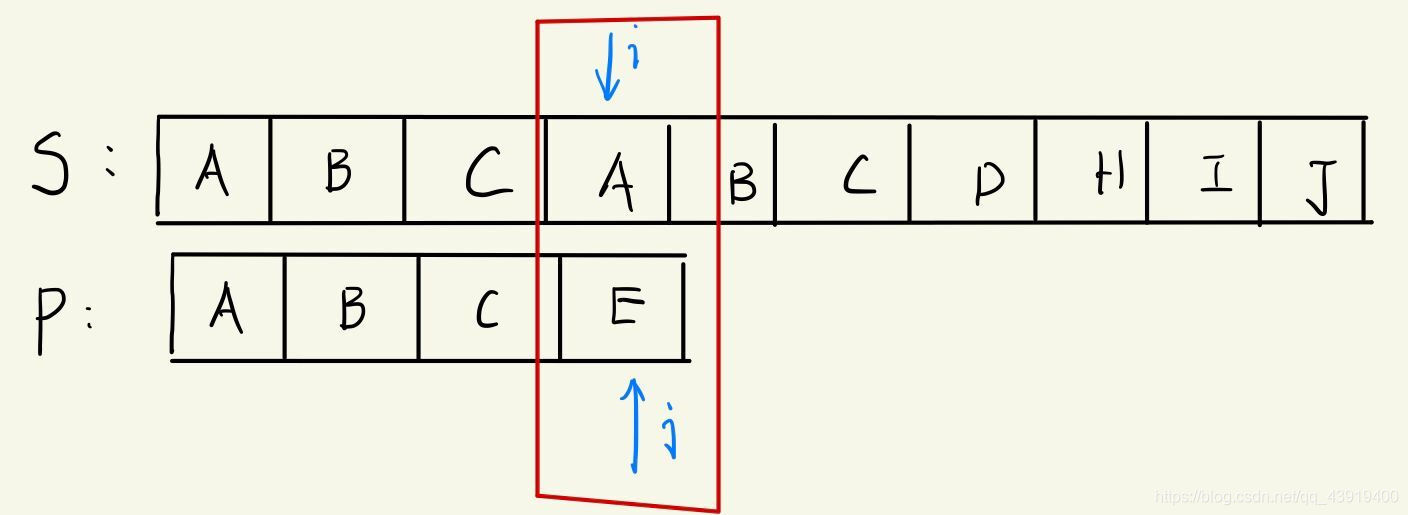
A教授：“如果按照之前cat同学所说，在这里我们遇到了不匹配，那么我们应该把j回退到0的位置，然后i退到1，这样合理吗？动动我们的大脑”。

cat：“这样不合理老师，我知道我错了。如果用我们人脑来计算的话，我看到前面ABC我就不会把子串P的A移动去对齐S的第一个B，因为显然是不匹配的，我会直接这样移动：”

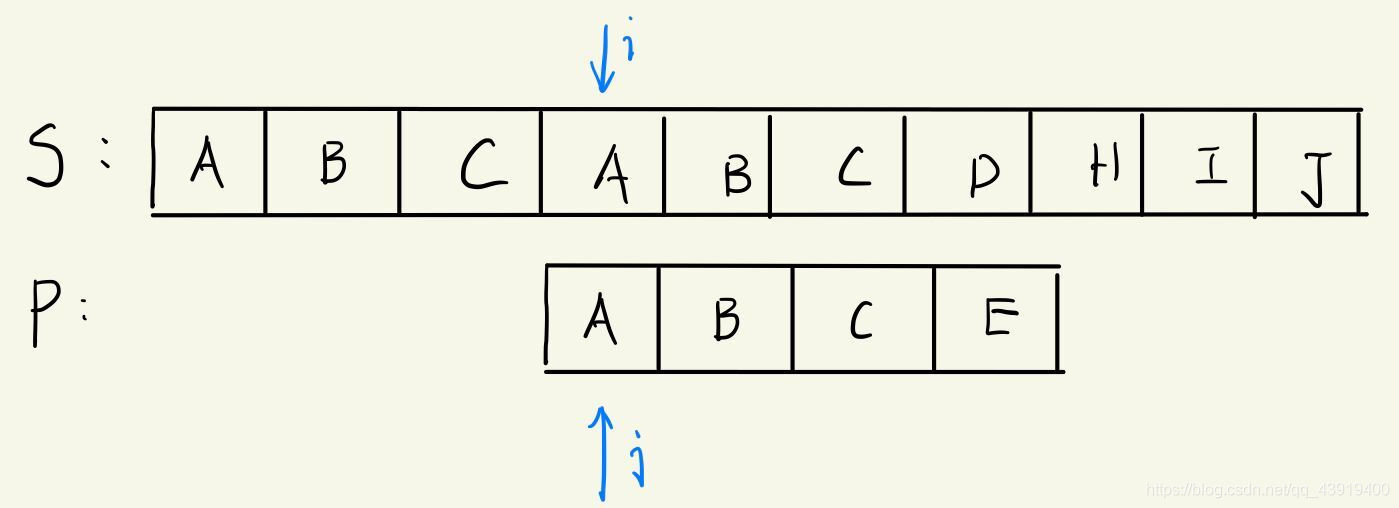
A教授：“是的，那你们有想过为什么是这样的吗？我们只需要移动子串，而不需要移动主串，当不匹配的时候，我们应该移动到子串的哪一个位置呢？让我们一起观察吧。”

说完之后老师在黑板上又画了一个图：

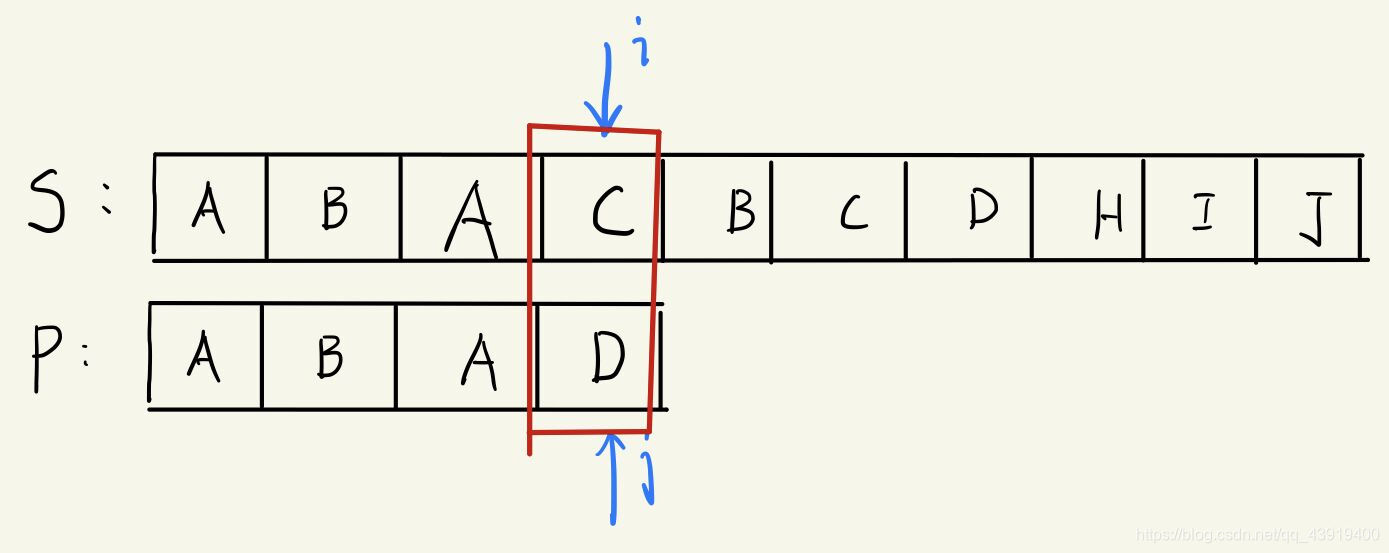
A教授：“大家看看，现在我们出现了不匹配的情况，那么哪一位同学能上黑板上来说说，如果只移动子串，那么我们应该把j移动到哪里一个位置呢？”

思考线：

cat陷入了沉思，脑海中出现了这样的画面：

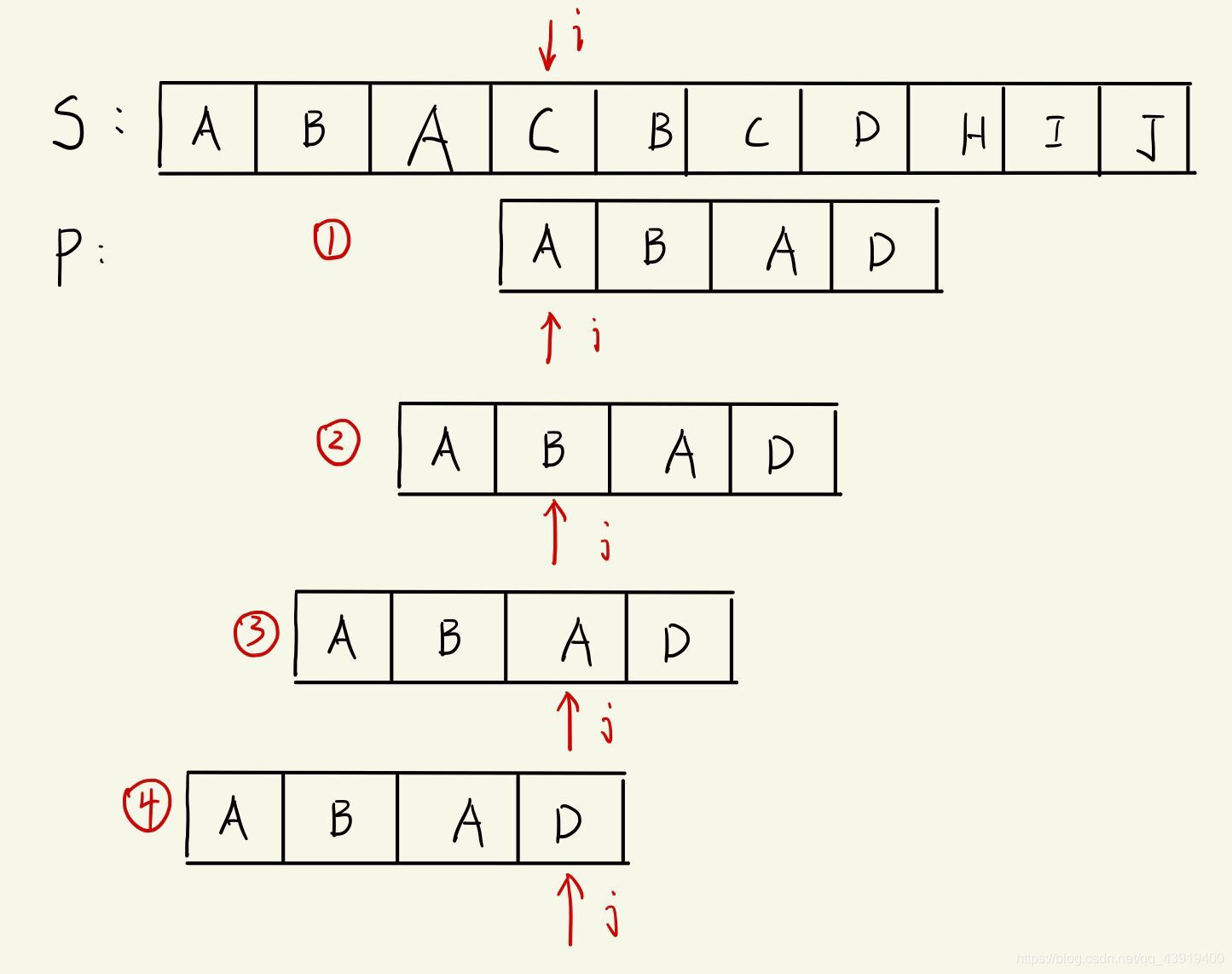
如果移动的情况是（1），那么显然不匹配，之后就会继续去寻找下一个位置，而且这样的移动毫无逻辑，匹配结果还会出现问题。
如果是（2），会不会出现匹配结果出错的可能性呢。我们看到之前主串的第一个A和子串的第一个A匹配失匹了（指从子串的第一个开始比较没有完成最终的匹配），所以断定P中第一个A不能和S中第一个A在一个位置。那P中的第一个A应该在哪里呢，因为之前匹配过所以可以看到S中还有第二个A，把P移动到这里，这样我们可以看到少比较了前面的A字符。
那可不可以是（3）呢，直接移到第二个A的位置，一看就不可以，因为这样移动前面就早已经不匹配了呀，指针怎么还可能在第二个A的位置呢。
那（4）的情况呢，不就和（3）一样嘛，前面就已经不匹配了。

cat经过脑中暴力的枚举，于是举手到黑板上，换下了如下的图形：

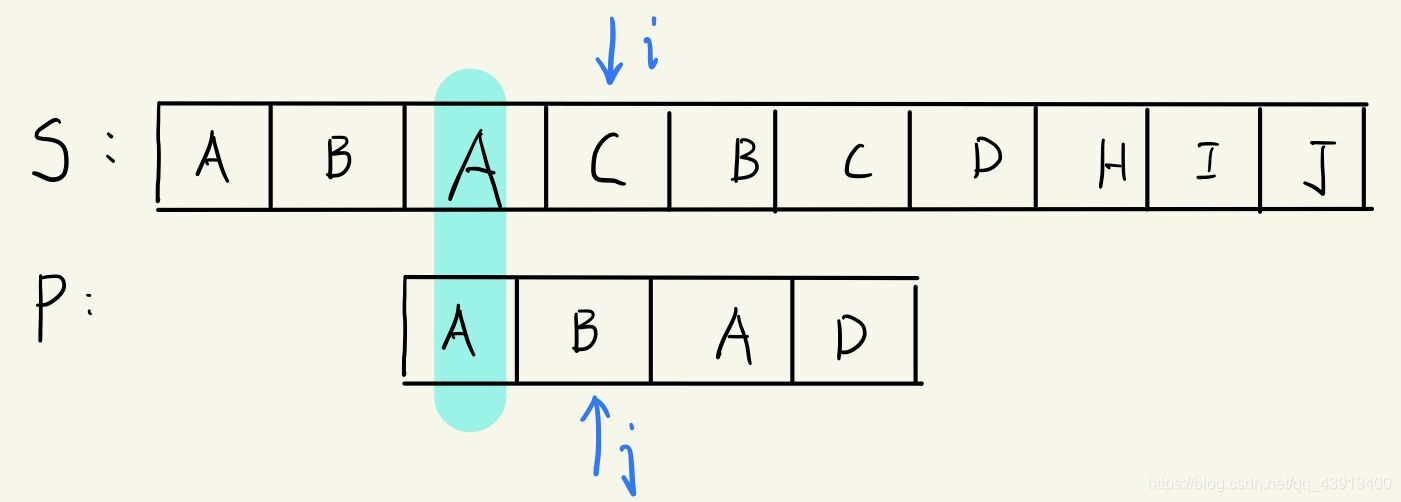
并且假装做了解释：“这里将子串移动到B的位置，这样前面的A不用匹配，因为由于前面的记忆我们知道这个A本来就是和主串匹配的。”，说完潇洒离去。

A教授抬了抬眼镜框，又在黑板上花了一个例子，“请大家再次找一找规律”，说完，戏谑的看向同学们。

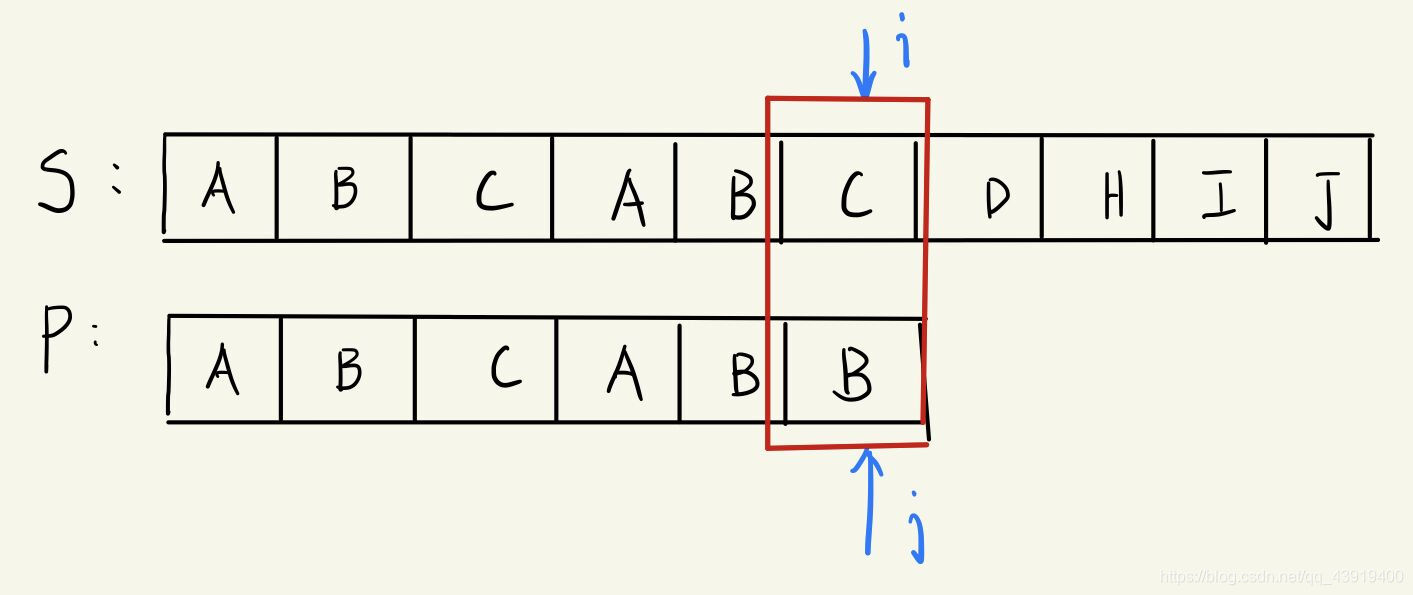
cat看向黑板，这里C、B位置出现不配了，那么子串的j应该移动到哪里呢？先不要暴力搜索，找一找规律看看。说完cat看向黑板。

“按照我之前的操作，我可以在心里试着向右平移P，看看到哪一个位置合适：开始！移动一位，首位A和主串B不匹配；再移动一位，首位A与主串C不匹配；再移动一位，匹配了！！！那如果再移动一位呢，不配了！”所以正确的位置应该是把j移动到C的位置，这样前面的AB因为是相同的，就不需要比较了。可是这个相同时因为和主串有关系吗？，不对，即使换一个主串，当我在最后一个B出现不匹配的时候，我都可以把指针移动到C的位置，因为C之前的字符串和之后的字符串都是AB，他们都是相同的。第一次AB比较说明两个情况，（1）第一个AB与主串前面的是匹配的，第二个AB与主串也是匹配的，（2）从第一个AB开始那么一定不能匹配。所以给我什么启发呢？

cat继续思考，那么肯定可以试试第二个AB可不可以匹配，而且我也不需要再次去比较第二个AB，因为他们在之前的记忆里面本来就是匹配的，所以指针直接指向C就好了。

cat再次举手，“老师，应该将j指针移动到C的位置”。例如这样：

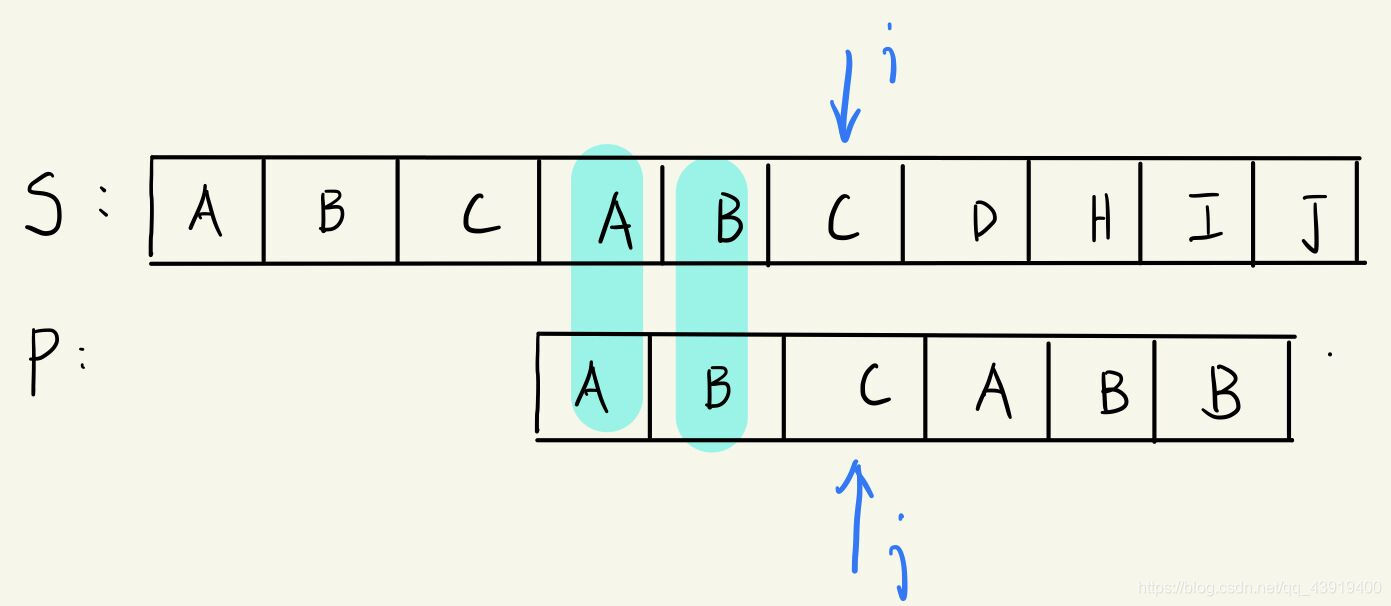
A教授微笑着示意cat坐下，但又想试试这个最强学生的实力，“cat，你能够带领我们一起找出为什么这样移动子串指针的规律吗？”。

说完，cat吃了一块巧克力，说着“~~我是要成为海贼王的男人~~”（走错片场了），然后走到黑板上。

最强分割线：

“其实我们这里移动j的位置和主串没有任何的关系，而仅仅和我们的子串有关系，当出现不匹配，应该把j移动到哪一个位置，其实你会发现是去找某个位置k，k之前和k之后有相同的位置，正如我上面思考的一样。首先它们都是已经得证在主串里面是有匹配对象的，而且前一个位置必然不匹配，那么我们就会想办法移到到k，让子串的前k和主串后k个比较，这样才就少比较了几个，节约时间”。

“等等，我这样说的话大家还是不明白，我自己都绕进去了，让我用数学表达式来展示一下”。

要移动的k的位置有这样的性质：最前面的k个字符和j之前的k个字符是相同的（这样我们移动到k的位置可以少比较k个字符），表达式如下：

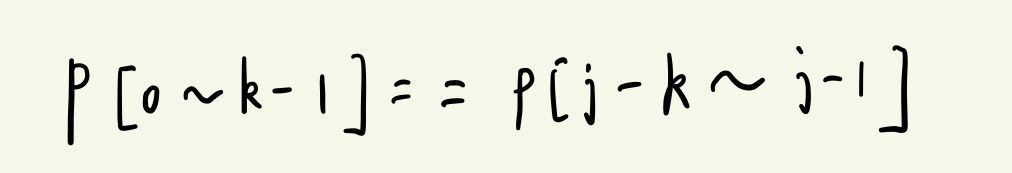
有这样的性质就可以证明我们是可以直接移动k，而不需要比较前面k个字符的：

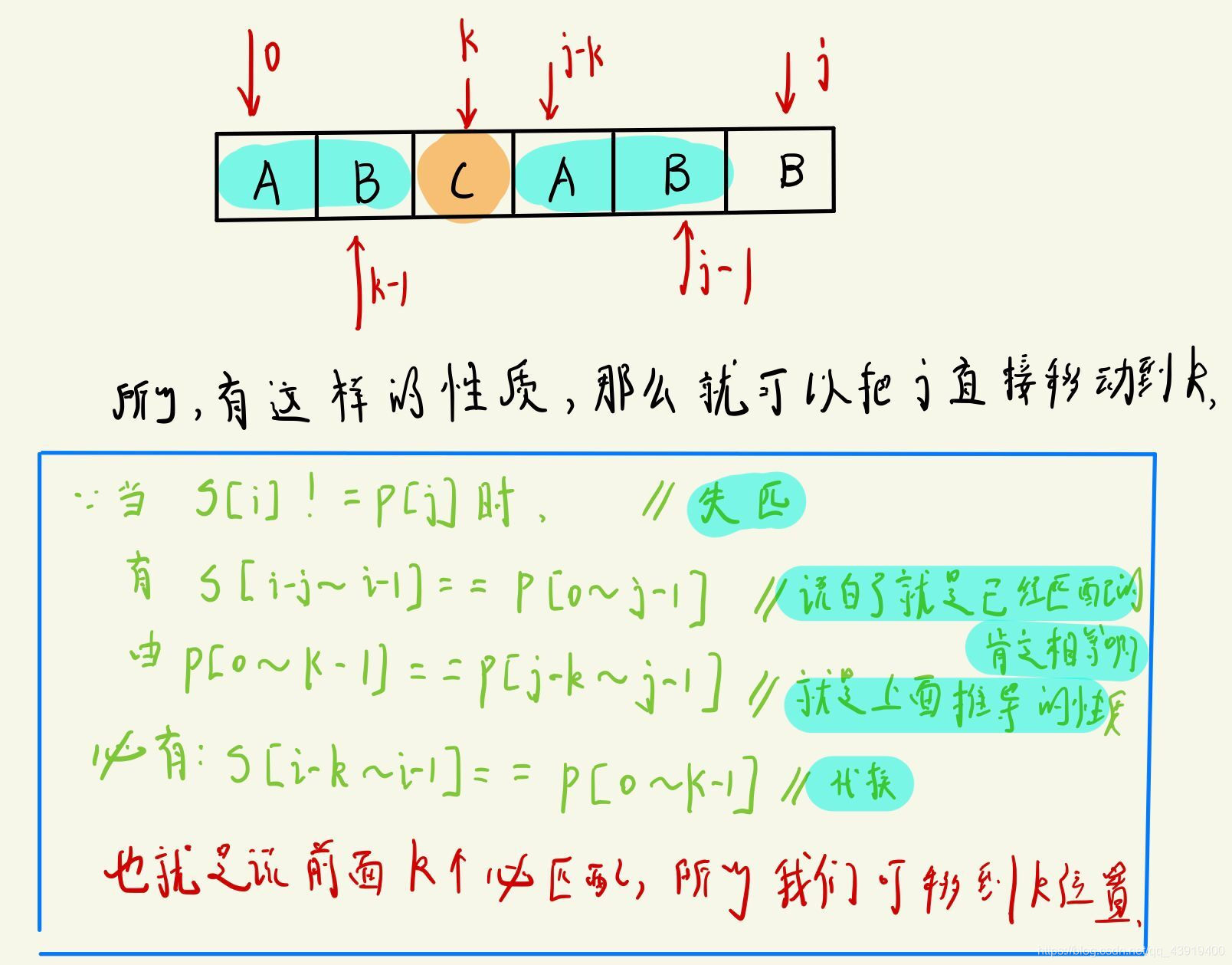
上面的证明其实只是想说因为j之前的k个相等，那么主串i之前的k个字符肯定和k之前的k歌字符相等，也就不用比较了（注意这里k依旧是数组小标，最小为0）。

cat说完，班上响起了一片掌声（不知道听没听懂，鼓掌就完事）。

“所以我们发现，我们只需要找到模式串中当不匹配时j移动的位置k就好了，这里我们可以用next数组来保存它（言简意赅，next意为下一个k的位置）”cat帅气拿起粉笔，开会板书。

黑板内容：

首先给出next[j]详细的定义：表示当P[j]!=S[i]时，j指针的下一步移动的位置。接下来我们就是去找next的值......
1、当我们第一个就不匹配，也就是next[0]是多少？显然子串不能够向后移动了，所以我们的i++，j的0和i=1比较。（这里就定义next[0]=-1，用来表示这个特殊的情况）

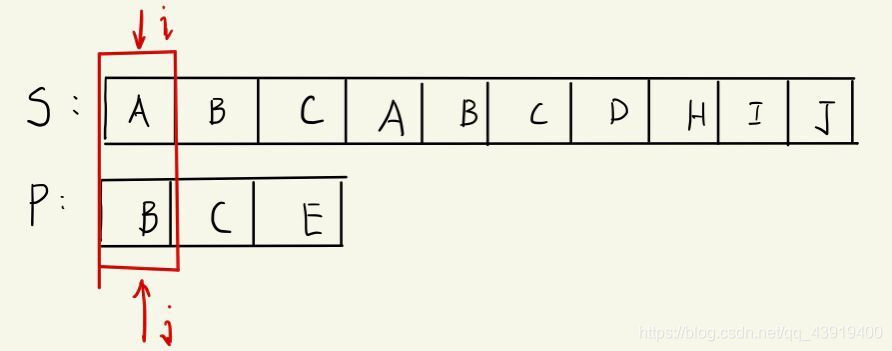
2、next[1]的值呢？

我们j需要向后移动，移动到哪里呢？肯定只能移到到第一位啦，因为也没有位置可以移动了，所以next[1]=0】。

3、那么next[2]、next[3]呢？（这是最重要的内容！！！）我们肯定是要根据已知的next值来推导后面的next值，所以一起看看...

首先我们来看看下面这张图片，说完cat就画了如下图：

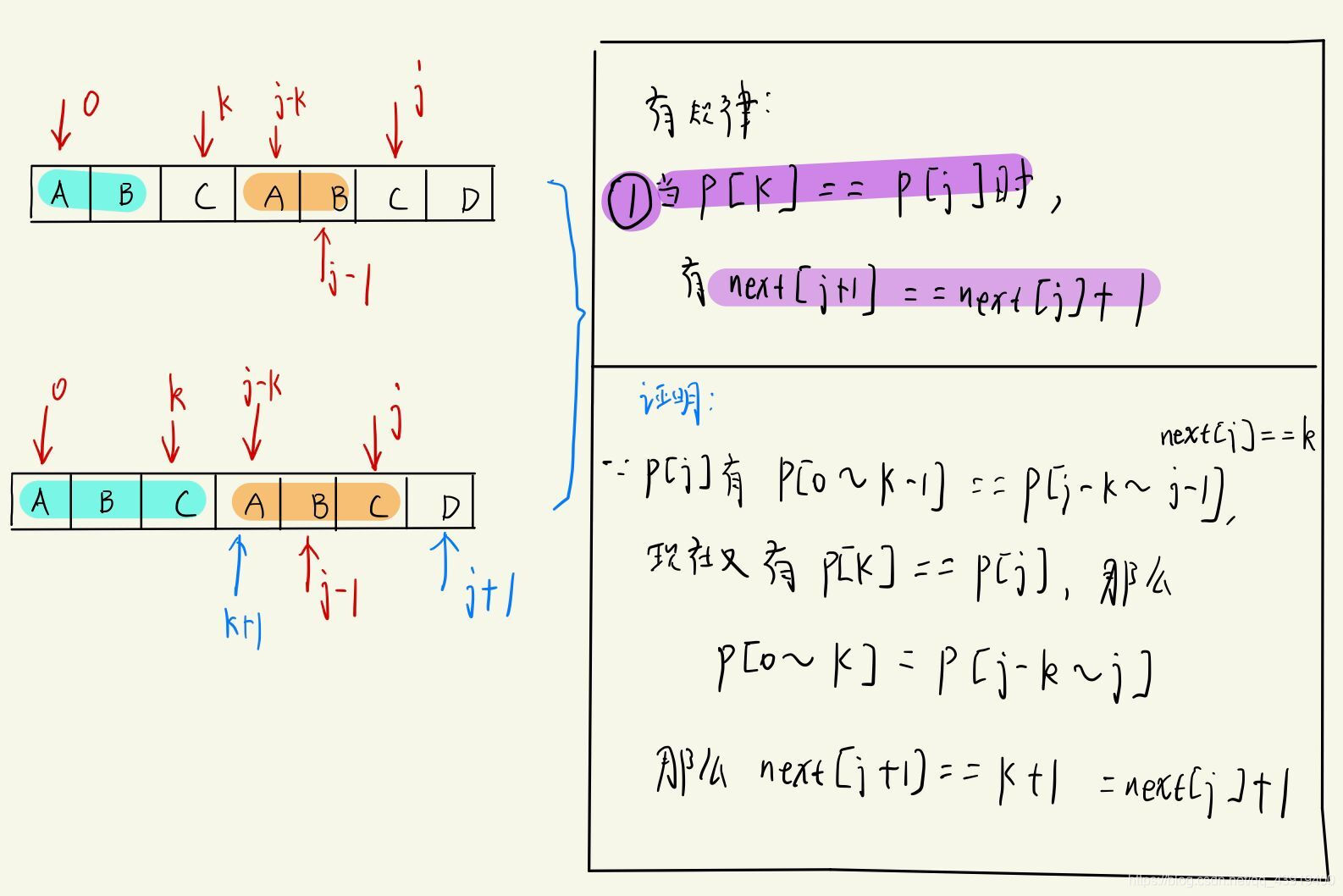
如果P[k]==P[j]，那么有next[j+1]==next[j]+1。如果不等于呢？

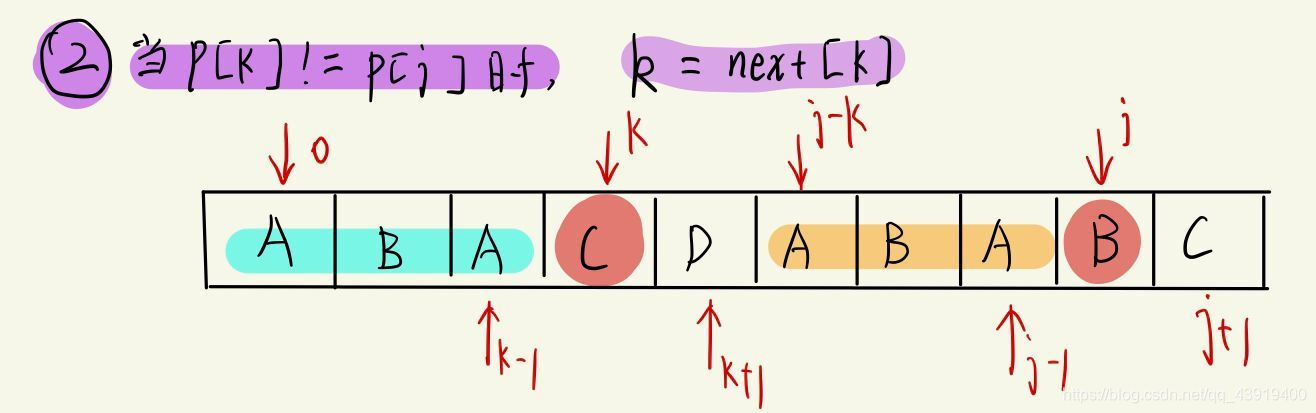
我们看到上面的图片中，就出现了P[k]!=P[j]的情况，指针k怎么移动呢？不清楚对吧，那么我们继续看看下面这张图片！

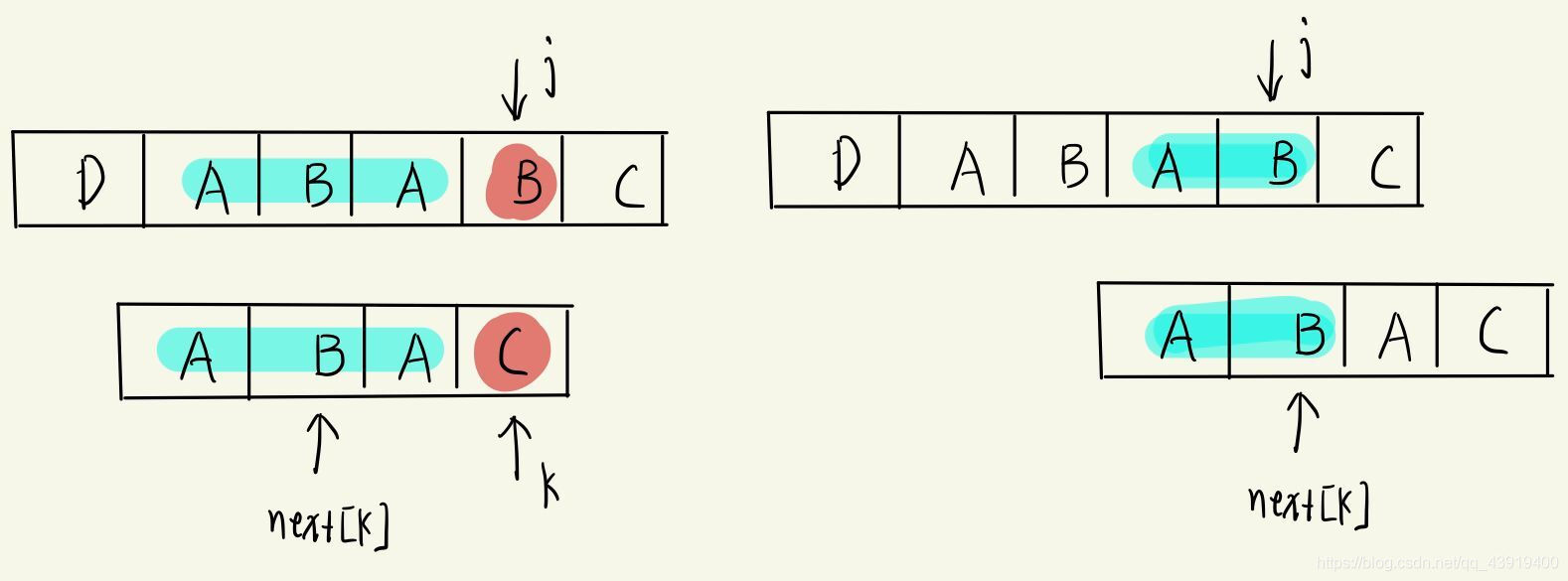
上面的图片是模式串自己的匹配，如果j不匹配，那么我们肯定移动到k的位置，而如果是j+1不匹配需要移动的位置就会发现因为P[i]、P[j]不相等，所以就不会存在子串这里也就是ABAC，所以不可能像之前一样将k的位置移动到D处，这样前面肯定不匹配呀。所以我们需要照到上图中移动可以匹配的位置，也就看到有最长的子串AB，移动到B的位置前面肯定匹配（右边图），所以k=next[k]。

所以我们就可以写出求一个模式串的next数组了，有：


void getNext(string p，int next[]) {
	next[0] = -1;//初始化，当在第一个位置不匹配定义为-1
	int k = -1;//当不匹配时移动的k的位置 
	int j = 0;//模式串的位置
	while(j<p.length()-1) {
		if(k==-1||p[j]==p[k]) {
			next[++j] = ++k;//P[j]==P[i]时，下一个next数组的值就是当前next值加一 
		} else {
			k = next[k];//P[i]!=P[j]是，next数组的值为next[k] 
		}
	}
}

仔细一看，不正是对应上面说过的情况嘛，先初始化，然后p[i]==p[j]和p[i]!=p[j]的情况都有了。

那么之前我用BF算法，现在可以改一改了，之前如果不匹配的话主串移动，子串也移动，现在主串不用移动，我们主需要子串移动就好。

所以改进的匹配算法就有：

int Kmp(string s,string p) {
	int i = 0;//主串的位置
	int j = 0;//子串的位置
	while(i<s.length()&&j<p.length()) {
		if(j==-1||s[i]==p[j]) {//j为-1也就是在第一个位置就不匹配对吧，所以j归零
			i++;
			j++;
		} else{//不匹配
            //i = j-i+1;
			j = next[j];//j归0 
		} 
	}
	if(j==p.length()){
		//子串走完了，匹配成功 
		return i-j;
	} 
	return -1;
}

Perfect!？不！上面和之前的暴力相比仅仅是i不动，j回溯到next数组指定的位置而已。

三、情景三

A教授：“太棒了，但是你看看这种情况呢？”

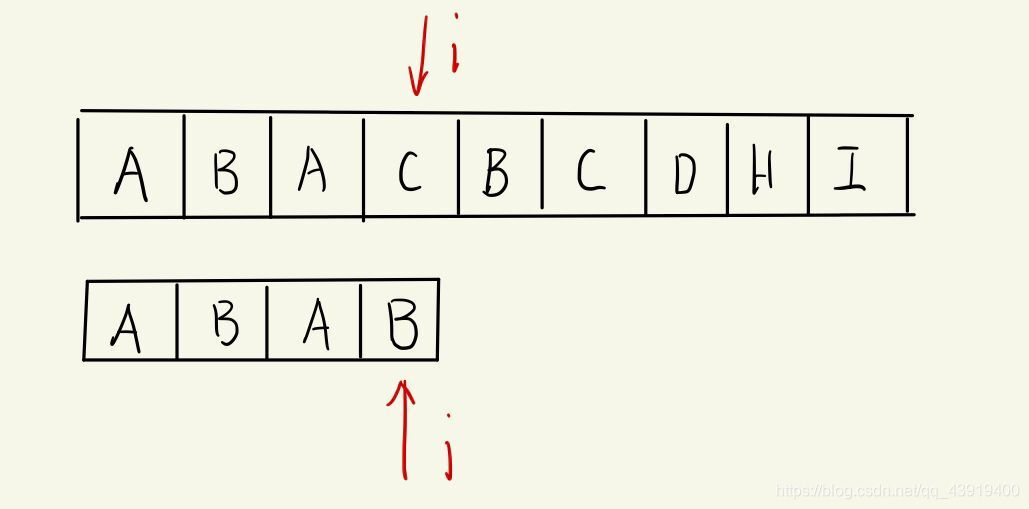
cat：“我们得到的next数组是：[-1,0,0,1]。所以现在遇到不匹配的情况我们应该退到k=1的位置，也就是这样”。

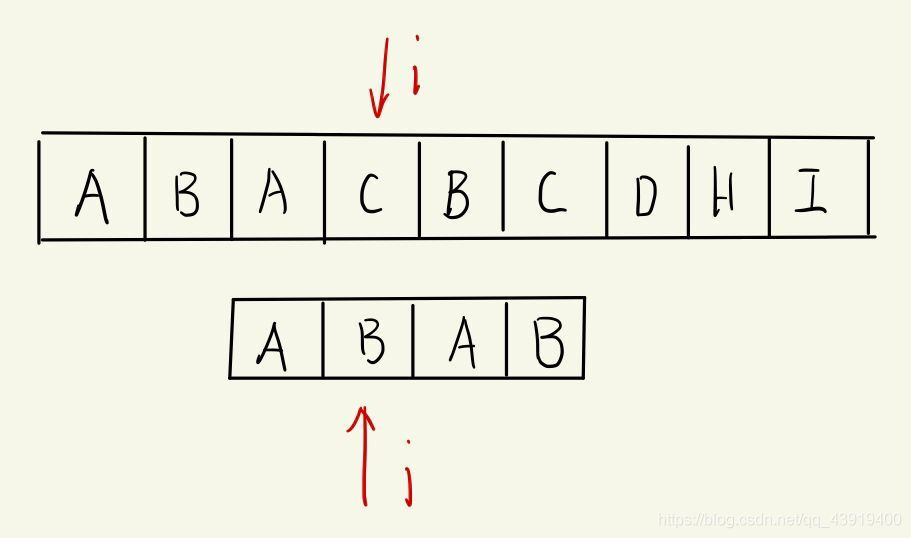
但是这里直接不匹配了，没有任何意义，也就是P[j]==P[next[j]]这种情况时，如果按照之前的next数组就浪费了，所以如果是这样的情况，我们就跳过它。所以getNext代码更改为：

void getNextVal(string p,int next[]) {
	next[0] = -1;//初始化，当在第一个位置不匹配定义为-1
	int k = -1;//当不匹配时移动的k的位置 
	int j = 0;//模式串的位置
	while(j<p.length()-1) {
		if(k==-1||p[j]==p[k]) {
			if(p[++j]==p[++k]) {
				next[j] = next[k];//这里跳过它，让next[k]赋值为next[j]
			} else {
					next[j] = k;//P[j]==P[i]时，下一个next数组的值就是当前next值加一 
			}
		} else {
			k = next[k];//P[i]!=P[j]是，next数组的值为next[k] 
		}
	}
}

A教授：“完美！”~