IEEE 754 浮点数

1. 定点数(Fixed Point Number)

2. 浮点数(Floating Point Number)

3. IEEE 754 标准

  3.1 什么是 IEEE 754

  3.2 IEEE 754 由来

  3.3 IEEE 754 构成

  3.4 IEEE 754 格式及编码

    （1）单精度浮点格式（32位）
    （2）双精度浮点格式（64位）

  3.5 格式化值与非格式化值

    （1）格式化值
    （2）非格式化值
    （3）特殊数值

  3.6 舍入误差

1. 定点数(Fixed Point Number)

---

  在计算机系统的发展过程中，业界曾经提出过许多种实数的表达方法，比较典型的是定点数。

  在定点数表达法中，其小数点固定地位于实数所有数字中间的某个位置。例如，货币的表达就可以采用这种表达方式，如 55.00 或者 00.55 可以用于表达具有4位精度(Precision)，小数点后有两位的货币值。由于小数点位置固定，所以可以直接用 4 位数值来表达相应的数值。

  但我们不难发现，定点数表达法的缺点就在于其形式过于僵硬，固定的小数点位置决定了固定位数的整数部分和小数部分，不利于同时表达特别大的数或者特别小的数。因此，最终绝大多数现代的计算机系统都采纳了所谓的浮点数表达法。

2. 浮点数(Floating Point Number)

---

  浮点数表达法采用了科学计数法来表达实数，即用一个有效数字(Significant)、一个基数(Base)、一个指数(Exponent)以及一个表示正负的符号(Sign）来表达实数。比如，123.45用十进制可以表达为 1.2345×10²——其中，1.2345 为有效数字，10 为基数，2 为指数。浮点数利用指数达到了浮动小数点的效果，从而可以灵活地表达更大范围的实数。其中，有效数字有时也称为尾数(Mantissa)。

  当然，对实数的浮点表示仅作如上的规定是不够的的，因为同一实数的浮点表示还不是唯一的。123.45 同样也可以表达为 0.12345×10³ 和 12.345×10¹这两种方式。正是因为这种表达的多样性，因此有必要对其加以规范以达到统一表达的目的。

  规范的浮点数表达方式具有如下形式：

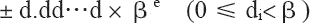
其中，d.dd…d为有效数字，β为基数，e为指数。

  有效数字中数字的个数称为精度，可以用 p 来表示有效数字精度。有效数字中的每个数字 d 介于 0（包括0） 和基数 β 之间，更精确地说，

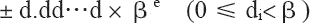
表示以下数：

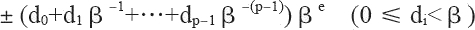
  其中，对十进制的浮点数，即基数 β 等于 10 的浮点数而言，如 12.345 可以表达为：1×10²+2×10¹+3×10⁰+4×10^-1+5×10^-2，则该十进制的浮点数的规范浮点数表达为 1.2345×10¹。

  同样地，对于二进制也可以如此简单地表达。唯一不同之处在于：二进制的 β 等于2，而每个数字 d 只能在 0 和 1 之间取值。如 1001.101，我们可以根据上面的表达式表达为：1×2³+0×2²