方格填数

题目描述

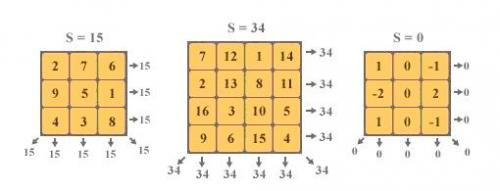
给一个n*n的方格矩阵，还有nn个整数，让你将这些整数填入矩阵，使得每行每列每个对角线上整数的和都相等。下面给出几个例子：

2 7 6 9 5 1 4 3 8

输入输出格式

输入格式：

第一行一个整数n.（1<=n<=4)

第二行n*n个整数 ai (-10^8<=ai<=108)

输出格式：

第一行一个整数s 代表每行每列每个对角线的和值

接下来输出一个n*n的矩阵，表示填数方案。

数据保证有解，可能存在多种方案，输出字典序最小的（将每行顺次相连之后，字典序最小）

输入输出样例

输入样例#1：

3
1 2 3 4 5 6 7 8 9

输出样例#1：

15
2 7 6
9 5 1
4 3 8

n乘n矩形只用搜索(n-1)乘(n-1)矩形即可

其余位置均可以通过已搜索位置确定

每一行的最后一列可以通过该行前(n-1)列之和确定

最后一行的第一列和最后一列需要满足对角线之和

其余列只用该列前(n-1)行之和确定

满足字典序 排序一下就行

#include<stdio.h>
#include<stdlib.h>
int n;
int a[20];
int used[20];
int ans[5][5];
int s;
int leap;
int comp(const void*a,const void*b)
{
	return *(int*)a-*(int*)b;
}
void search(int x,int y,int sum)      sum表示该行前(y-1)列之和
{
	int i,j,k;
	if(leap==1)
		return ;
	if(x==n&&y==n+1)
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=n;j++)
				printf("%d ",ans[i][j]);
			printf("\n");
		}
		leap=1;
	}
	else if(x==n)
	{
		int f=0;
		for(i=1;i<n;i++)
			f+=ans[i][y];
		for(i=1;i<=n*n;i++)
		{
			if(!used[i])
			{
				if(f+a[i]==s)
				{
					if(y==1)
					{
						int m=0;
						for(j=1,k=n;j<n;j++,k--)
							m+=ans[j][k];
						if((m+a[i])!=s)
							continue;
					}
					if(y==n)
					{
						int m=0;
						for(j=1,k=1;j<n;j++,k++)
							m+=ans[j][k];
						if((m+a[i])!=s)
							continue;
					}
					ans[x][y]=a[i];
					used[i]=1;
					search(x,y+1,sum);
					used[i]=0;
				}
			}
		}
	}
	else if(y==n)
	{
		for(i=1;i<=n*n;i++)
		{
			if(!used[i])
			{
				if(sum+a[i]==s)
				{
					ans[x][y]=a[i];
					used[i]=1;
					search(x+1,1,0);
					used[i]=0;
				}
			}
		}
	}
	else
	{
		for(i=1;i<=n*n;i++)
		{
			if(!used[i])
			{
				ans[x][y]=a[i];
				used[i]=1;
				search(x,y+1,sum+a[i]);
				used[i]=0;
			}
		}
	}
}
int main(void)
{
	int i;
	scanf("%d",&n);
	for(i=1;i<=n*n;i++)
	{
		scanf("%d",&a[i]);	
		s+=a[i];
	}
	qsort(a+1,n*n,sizeof(int),comp);
	s/=n;
	printf("%d\n",s);
	search(1,1,0);
}