最大的公共字符串

问答题

问答题1：二叉树遍历
某二叉树的前序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为？

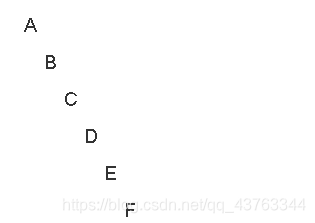
这个还是感觉不太友好，第一次还没想到有这种情况的二叉树，这也是一种固化思维，以为所有的二叉树都必须要有左右子树；上图的这种情况前序中序遍历都一样，层序遍历也是一样的，但是后续遍历是:FEDCBA；

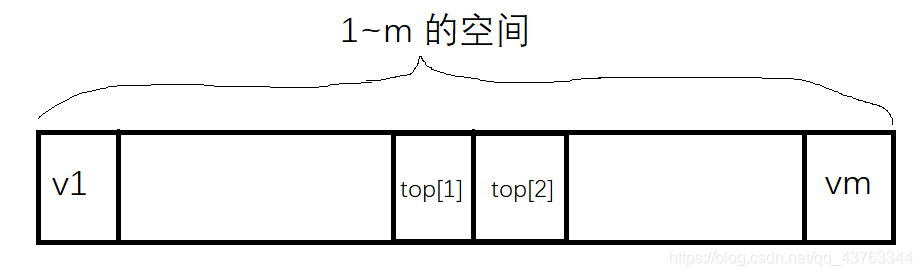
问答题2： 若栈采用顺序存储方式存储，现两栈共享空间V[1…m]，top[i]代表第i个栈( i =1,2)栈顶，栈1的底在v[1]，栈
2的底在V[m]，则栈满的条件是？

(A) top[1]+top[2]=m
(B) top[1]+1=top[2]
(C) top[2]-top[1]|=0
(D) top[1]=top[2]

提示：v₁到 top[1]表示栈1的空间，v_m到top[2] 表示栈2的空间，所以当top[1] + 1 == top[2]的时候，栈满.

问答题3：某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为？

提示：有二叉树计算公式，叶子节点为度为2的节点个数+1

答案：200

问答题4：在具有 2n 个结点的完全二叉树中，叶子结点个数为?

提示：完全二叉树是指除最后一层外，每一层上的结点数均达到最大值，在最后一层上只缺少右边的若干结点

根据完全二叉树性质，如果共 2n 个结点，从根结点开始按层序用自然数 1 ， 2 ，…， 2n 给结点编号，则编号为 n 的结点左子结点编号为 2n ，因此叶子结点编号为 n+1,n+2, … ,2n ，故叶子结点个数为 n

总结：如果节点数n为偶数，则在完全二叉树里叶子节点为 n/2,如果为奇数则叶子节点为 n/2+1

问答题5：为提高散列（Hash）表的查找效率，可以采取的正确措施是？
Ⅰ．增大装填（载）因子
Ⅱ．设计冲突（碰撞）少的散列函数
Ⅲ．处理冲突（碰撞）时避免产生聚集（堆积）现象

提示：装填因子的计算公式为=关键字个数 / 表长度 这个装填因子和hash表的平均查找长度有关。如果要增大装填因子显然要么增加关键字个数，要么减少表长度，这两种方式都只会导致更多冲突的产生

答案：Ⅱ、Ⅲ

问答题6： 将整数数组（7-6-3-5-4-1-2）按照堆排序的方式原地进行升序排列，请问在第一轮排序结束之后，数组的顺序是？

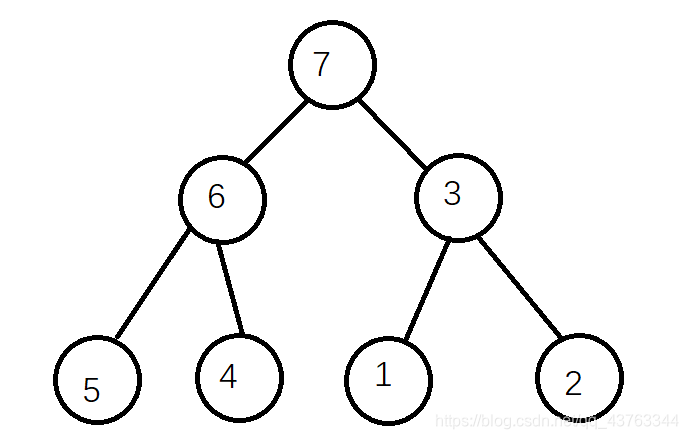
堆排序的顺序

第一步：将堆顶元素和最后一个元素交换
第二步：删除最后一个元素(这里指的是把最后一个元素放到了最后的位置)
第三步：调整新的堆结构
第四步：重复第二、三步

那么第一轮结束后，得出的堆结构为

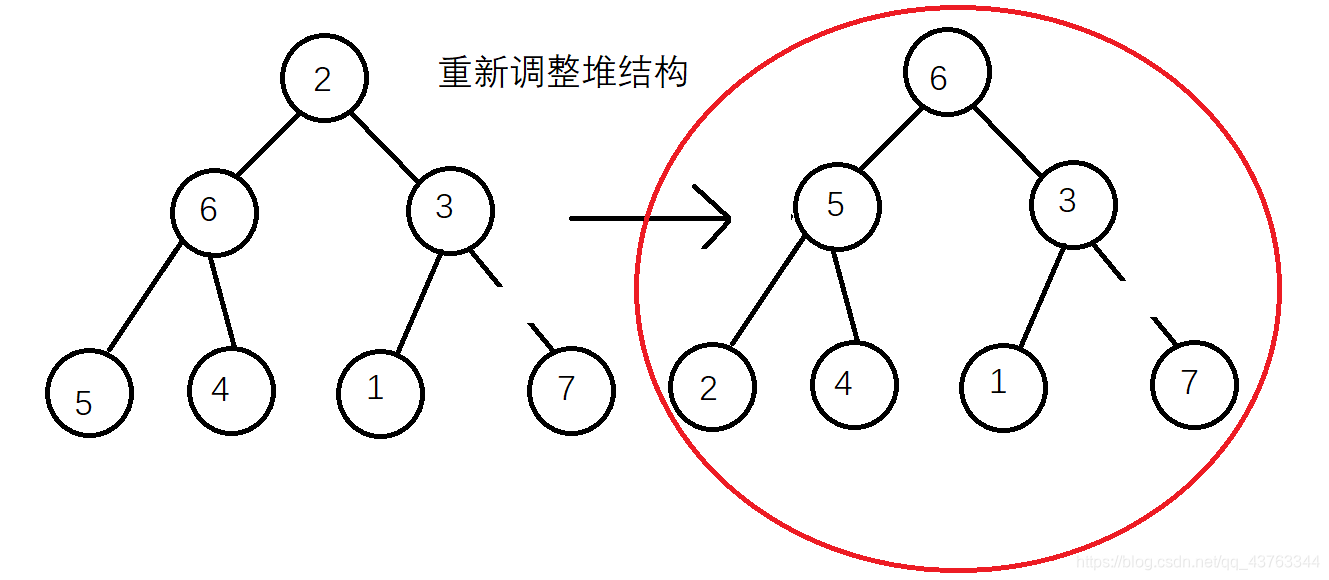
答案：6532417

问答题7：要连通具有 n 个顶点的有向图，最少需要几条边？

提示：连通就是要能走通，对于有向图来说，就是 n 条边，如果是无向图n-1条边就行了.

编程题

编程题1：公共字符串

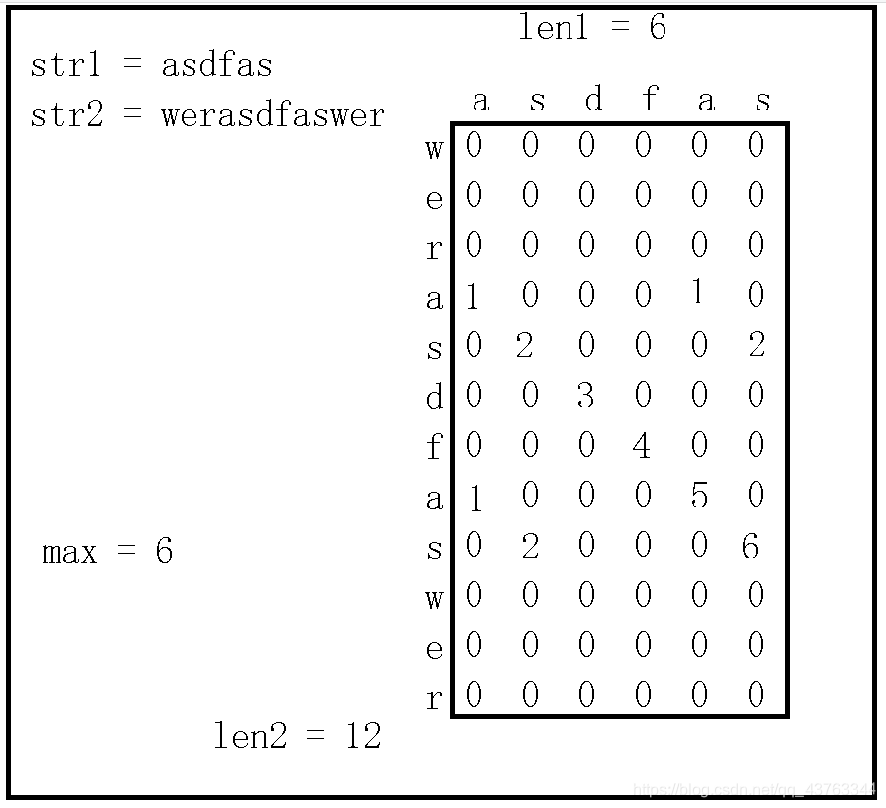
计算两个字符串的最大公共字串的长度，字符不区分大小写

例:
输入 asdfas werasdfaswer
输出 6

#include<iostream>
#include<vector>
#include <string>
using namespace std;

int main(){
	int max = 0; //max初值.
	string str1, str2;
	while (cin >> str1 >> str2){
		int len1 = str1.size();
		int len2 = str2.size();
		int max = 0;
		//所有值初始化为0
		vector<vector<int>> dp(len1, vector<int>(len2, 0));
		for (int i = 0; i < len1; i++){
			for (int j = 0; j < len2; j++){
				//如果当前结尾的字符相等，则在dp[i-1][j-1]的基础上加1
				if (str1[i] == str2[j]){
					if (i >= 1 && j >= 1)
						dp[i][j] = dp[i - 1][j - 1] + 1;

					else
						//dp[i][0] or dp[0][j]
						dp[i][j] = 1;
				}
				//更新最大值
				if (dp[i][j] > max)
					max = dp[i][j];
			}
		}
		cout << max << endl;
	}
	return 0;
}

编程题2：洗牌

洗牌在生活中十分常见，现在需要写一个程序模拟洗牌的过程

现在需要洗2n张牌，从上到下依次是第1张，第2张，第3张一直到第2n张。首先，我们把这2n张牌分成两堆，左手拿着第1张到第n张(上半堆)，右手拿着第 n+1 张到第 2n 张(下半堆)

先放下右手的最后一张牌，再放下左手的最后一张牌，接着放下右手的倒数第二张牌，再放下左手的倒数第二张牌，直到最后放下左手的第一张牌.

接着把牌合并起来就可以了。 例如有6张牌，最开始牌的序列是1,2,3,4,5,6。首先分成两组，左手拿着1,2,3；右手拿着4,5,6。在洗牌过程中按顺序放下了6,3,5,2,4,1。把这六张牌再次合成一组牌之后，我们按照从上往下的顺序看这组牌，就变成了序列1,4,2,5,3,6。 现在给出一个原始牌组，请输出这副牌洗牌k次之后从上往下的序列

输入描述：第一行第一个数 T 表示数据组数，对于每组数据，前两个数为 n , k ；n代表每组数字的个数，k 代表洗牌的次数

输出描述：对于每组数据，输出一行，最终的序列。数字之间用空格隔开，不要在行末输出多余的空格

输入
3 3 1 1 2 3 4 5 6 3 2 1 2 3 4 5 6 2 2 1 1 1 1
输出
1 4 2 5 3 6 1 5 4 3 2 6 1 1 1 1

//3组
//第一组 3 1 
//      1 2 3 4 5 6
//第二组 3 2
//      1 2 3 4 5 6
//第三组 2 2 
//      1 1 1 1
#include <iostream>
#include <vector>
using namespace std;

int main(){
    int t,n,k;
    // 一共有t组数据
    cin>>t;
    while(t--){
        cin>>n>>k;
        int num = 2*n;
        vector<int>table(num);
        for(int i=0;i<num;++i){
            cin>>table[i];
        }
        //洗牌
        while(k--){
            vector<int>n1(table.begin(),table.end());
            for(int i=0;i<n;++i){
                table[2*i] = n1[i];
                table[2*i+1] = n1[i+n];
            }
        }
        // 输出洗好后的牌
        for(int i=0;i<num-1;++i){
            cout<<table[i]<<' ';
        }
        cout<<table[num-1]<<endl;
    }
    return 0;
}