Dijkstra算法详解-优快云博客

转载

——————————————

Dijkstra算法思想

如果图是不带负权的有向图或者无向图，我们可以利用贪心策略，从起点s每次扩展一个距离起点s最短的点，并且利用这个点，更新起点到其他点的距离。

Dijkstra算法流程

1、用一个数组a[i]记录其它点到起点s的最短距离，用一个数组b[i]标记是否得到从起点s到点i的最短距离
2、初始化数组a[i]，修改其它点到起点s的距离，其中a[s]=0（起点到起点的距离为0），其他a[i]=∞（无限大）
3、选择一个没有被标记的点k并且d[k]的值是最小的
4、如果找不到，退出
5、标记点k，b[k]=true;
6、以k为中点，修改其他点到起点s的距离

Dijkstra算法流程模拟

下面用一个实例来具体说明：
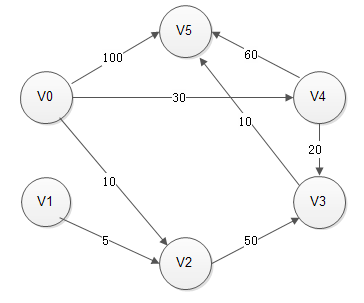
在这里插入图片描述
（1）V0-V5 共6个节点，节点间路径已标出，现要求从V0到其余各节点的最短路径；
（2）有上面的算法流程可知，在使用Dijkstra算法时需要几个结构来保存我们想要的信息：
1.保存这张图的结构体
2.记录V0到其余各节点最短路径的数组（这里设为len[n+1]）
3.记录某节点是否已找到最短路径的数组（这里设为note[n+1]）
（3）接下来就是算法实现部分：
1.标记note[V0]=true;初始化 Len[]={0,∞,0,∞,10,∞,30,100}

2.第一次循环与V0相邻的有V2、V4、V5，其中V2距离最短为10，标记V2，并且以V2为中间点（路径为V0->V2->Vx）更新最短路表,此时V3被更新为10+50=60。

3.进入第二次循环，此时未被标记的有V1、V3、V4、V5,，其中从V0到这些的临时最短路分别为∞、60、30、100，从中找到最小的即V4，将V4标记为1，以V4为中间点（路径为V0->V4->Vx）更新最短路表，此时V3被更新为50，V5被更新为90。

4.进入第三次循环，此时未被标记的有V1、V3、V5，其中临时最短路分别为∞、50、90，从中找到最小的即V3，将V3标记为1，以V3为中间点（路径为V0->V4->V3->Vx）更新最短路表，此时V5被更新成60。

5.进入第四次循环，此时未被标记的有V1、V5，其中临时最短路分别为∞、60，找到V5，标记为1，以V5为中间点更新最短路表，此时没有元素被更新

6.进入第五次循环，这次循环没找到任何东西

7.退出循环，Len表中即为V0到其余各个节点的最短路径。

Dijkstra模板例题（没有优化O（n²））

题目来源：https://www.luogu.org/problemnew/show/P2299
【题目描述】
从1城市到n城市有很多条路，经过每条路所用的时间有可能不同，请问从1城市到n城市至少需要多少时间
【输入输出格式】
【输入格式】：
第一行有两个数n，m。n表示有n个停留站，m表示共有m条路。
之后m行，每行三个数ai bi ci，表示第ai个停留站到第bi个停留站需要ci的时间。（无向）
【输出格式】：
一行，输出1到n最短时间。
【输入输出样例】
【输入样例】
5 8
1 2 3
2 3 4
3 4 5
4 5 6
1 3 4
2 4 7
2 5 8
1 5 100
【输出样例】
11
【说明】
时空限制：1000ms,128M
数据规模：
n≤2500 m≤2∗10的5次方

Dijkstra模板例题程序：

//Dijkstra
//https://www.luogu.org/problemnew/show/P2299
#include<fstream>
#include<cstring>
#include<iostream>
#define xb 2505
using namespace std;
int n,m,x,y,v;
int xy[xb][xb];
bool ifx[xb];//标记每个点最短路有没有被确定 
int weight[xb];//每个点到1城市的最小值 
void begin()
{
    memset(weight,0x7f,sizeof(weight));//把每个城市到1城市的所用时间调到最大
    weight[1]=0;//1到1的最小值为0 
    for(int i=1;i<=n;i++)
    {//初始化每个点到点1的值 
        weight[i]=xy[1][i];
    }
    ifx[1]=true;//1的最短路径已被确定
}
void Dijkstra()
{
    begin();//初始化
    for(int i=2;i<=n;i++)
    {
    	//打擂台找哪个城市到1城市所用的时间最少且这座城市的最短路径还没被确定 
        int num=0,sum=weight[0];
        for(int j=1;j<=n;j++)
        {
            if(!ifx[j]&&weight[j]<sum)
            {
            	sum=weight[j];
            	num=j;
            }
        }
        //如果找不到城市，退出 
        if(!num)break; 
        ifx[num]=true;//标记 
        for(int j=1;j<=n;j++)
        {
        	if(xy[num][j]+weight[num]<weight[j])
        	{//修改最短路径 
        		weight[j]=weight[num]+xy[num][j];
            }
        }
    }
}
int main()
{
    memset(xy,0x7f,sizeof(xy));//先调到最大值 
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
    	scanf("%d%d%d",&x,&y,&v);
    	if(v<xy[x][y])//x到y可能有很多条道路，要找出最小值 
    	xy[x][y]=xy[y][x]=v;
    }
    Dijkstra();
    printf("%d",weight[n]);
    return 0;
}

【堆优化】
题目：https://www.luogu.org/problem/P4779

#include<queue>
#include<fstream>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int n,m,s,f;
int next[200005],one[200005],g[200005],w[200005];
LL weight[100005];
bool note[100005];
priority_queue<pair<int,int> >q;
void Dij()
{
	memset(weight,0x7f,sizeof(weight));
	weight[s]=0;
	q.push(make_pair(0,s));//优先队列排序第一个优先级更高，顺序不能乱
	while(q.size())
	{
		int now=q.top().second;
		q.pop();
		if(note[now])continue;
		note[now]=true;
		for(int i=one[now];i;i=next[i])
		{
			if(weight[g[i]]>weight[now]+w[i])
			{
				weight[g[i]]=weight[now]+w[i];
				q.push(make_pair(-weight[g[i]],g[i]));
			}
		}
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&f,&g[i],&w[i]);
		next[i]=one[f];
		one[f]=i;
	}
	Dij();
	for(int i=1;i<=n;i++)
	{
		printf("%d ",weight[i]);
	}
	return 0;
}