常用的八种排序算法——Java实现_排序算法全局有序性-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43722914/article/details/112547989

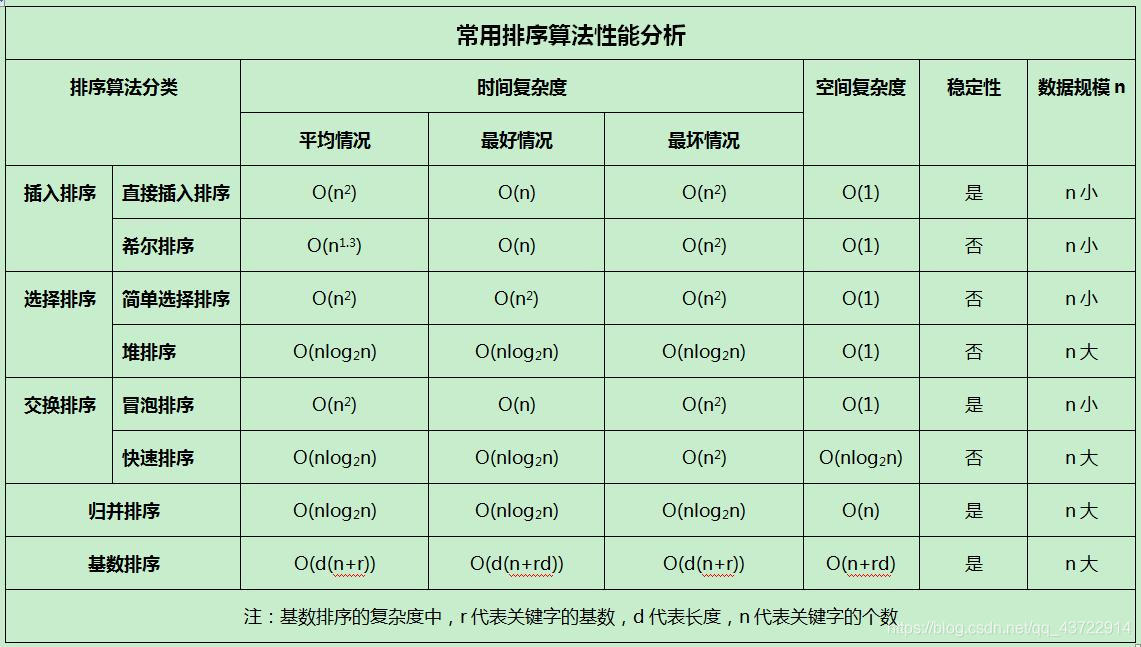
算法性能对比

000000

插入排序

直接插入排序

思想

实现思路：初始构建有序区，对于无序区的数据，在有序序列中从后向前扫描，找到相应位置并插入。
说明：每趟排序产生的有序区不一定是全局有序区。

实现

public class InsertSort {
    public static int[] insertSort(int[] arrays){
        if(arrays == null || arrays.length < 2){
            return arrays;
        }
        //抽取元素
        int tmp;
        //对每个元素进行抽取
        for (int i = 1; i < arrays.length; i++) {
            tmp = arrays[i];
            int j;
            for (j = i-1;j >= 0;j--){
                if(tmp >= arrays[j]) break;
                arrays[j+1] = arrays[j];
            }
            //将抽出元素插入
            arrays[j+1] = tmp;
        }
        return arrays;
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        arrays = insertSort(arrays);
        System.out.println(Arrays.toString(arrays));
    }
}

希尔排序

思想

实现思路：实际上是一种分组插入方法。先将整个待排序列分割成若干子序列分别进行直插排序、待整个序列基本有序以后，再对全体序列进行直插排序。
说明：每趟排序产生的有序区不一定是全局有序区。

实现

public class HillSort {
    public static int[] hillSort(int[] arrays){
        //初始增量
        int increment = arrays.length/2;
        //定义交换变量
        int tmp;
        //增量为0时 排序完成
        while (increment != 0){
            //选择排序
            for (int i = increment; i < arrays.length; i++) {
                tmp = arrays[i];
                int j;
                for (j = i-increment; j >= 0; j -= increment) {
                    if(tmp >= arrays[j]){
                        break;
                    }
                    arrays[j+increment] = arrays[j];
                }
                //将抽出元素插入
                arrays[j+increment] = tmp;
            }
            increment = increment>>1;
        }
        return arrays;
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(hillSort(arrays)));
    }
}

选择排序

简单选择排序

思想

排序思路：还是分为有序区和无序区，第一次默认都是无序区，每次排序把无序区里最小的元素换至无序区的第一位置，然后将其划入有序区，以此类推。
说明：每趟产生的有序区一定是全局有序区，因为每趟都能把一个元素归位。
优化：每次归位最小、最大两个元素。

实现

public class SelectSort {
    //双for循环排序 O(n^2)
    public static int[] selectSort(int[] arrays){
        if(arrays == null || arrays.length == 0){
            return arrays;
        }
        //记录最小元素的下标
        int index;
        //用于交换的临时变量
        int tmp;
        //遍历数组
        for (int i = 0; i < arrays.length; i++) {
            index = i;
            //遍历数组找到从当前位置及之后元素的最小元素
            for (int j = i+1;j < arrays.length;j++){
                if(arrays[index] >= arrays[j]){
                    index = j;
                }
            }
            //交换
            tmp = arrays[i];
            arrays[i] = arrays[index];
            arrays[index] = tmp;
        }
        return arrays;
    }

    //优化选择排序
    public static int[] optSelectSort(int[] arrays){
        if(arrays == null || arrays.length == 0){
            return arrays;
        }
        //记录最小元素的下标
        int minIndex;
        //记录最大元素的下标
        int maxIndex;
        //用于交换的临时变量
        int tmp;
        //遍历数组
        for (int i = 0; i < arrays.length>>1; i++) {
            minIndex = i;
            maxIndex = i;
            for (int j = i+1;j < arrays.length-i;j++){
                //找最小元素
                if(arrays[minIndex] > arrays[j]){
                    minIndex = j;
                    continue;
                }
                //找最大元素
                if(arrays[maxIndex] < arrays[j]){
                    maxIndex = j;
                }
            }
            //交换最小元素
            tmp = arrays[i];
            arrays[i] = arrays[minIndex];
            arrays[minIndex] = tmp;
            //当array[i]为最大元素时
            if(arrays[i] == arrays[maxIndex]){
                maxIndex = minIndex;
            }
            //交换最大元素
            tmp = arrays[arrays.length-1-i];
            arrays[arrays.length-1-i] = arrays[maxIndex];
            arrays[maxIndex] = tmp;
        }
        return arrays;
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        int[] arrays1 = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(selectSort(arrays)));
        System.out.println(Arrays.toString(optSelectSort(arrays1)));
    }
}

堆排序

思想

排序思路：一种树形选择排序方法，（以大根堆为例）第一次循环：将待排序序列构造成一个大根堆，此时，整个序列的最大值就是堆顶的根结点，将其与末尾元素进行交换，然后，末尾就为最大值。第二次循环：将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值，再将其与次尾元素交换。如此反复执行，便能得到一个有序序列了。
说明：堆排序每趟产生的有序区一定是全局有序区。

实现

public class HeapSort {
    
    public static int[] heapSort(int[] arr){
        if (arr == null || arr.length == 0) {
            return arr;
        }
        //构建大顶堆
        int length = arr.length;
        for (int i = (length>>1)-1; i >= 0; i--) {
            adjust(arr, i, length);
        }
        // 交换堆顶和当前末尾的节点，重置大顶堆
        for (int i = length - 1; i > 0; i--) {
            swap(arr, 0, i);
            length--;
            adjust(arr, 0, length);
        }
        return arr;
    }

    //调整
    protected static void adjust(int []arr,int index,int length){
        // 先根据堆性质，找出它左右节点的索引
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        // 默认当前节点（父节点）是最大值。
        int largestIndex = index;
        if (left < length && arr[left] > arr[largestIndex]) {
            // 如果有左节点，并且左节点的值更大，更新最大值的索引
            largestIndex = left;
        }
        if (right < length && arr[right] > arr[largestIndex]) {
            // 如果有右节点，并且右节点的值更大，更新最大值的索引
            largestIndex = right;
        }
        if (largestIndex != index) {
            // 如果最大值不是当前非叶子节点的值，那么就把当前节点和最大值的子节点值互换
            swap(arr, index, largestIndex);
            // 因为互换之后，子节点的值变了，如果该子节点也有自己的子节点，仍需要再次调整。
            adjust(arr, largestIndex, length);
        }
    }

    //交换
    protected static void swap(int[] arr,int index1,int index2){
        int temp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = temp;
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(heapSort(arrays)));
    }
}

交换排序

冒泡排序

思想

通过无序区中相邻元素之间的比较和位置的交换使最大的元素逐渐移动至待排序列的最后。
说明：每趟产生的有序区一定是全局有序区。
优化：如果在某一次循环中元素位置未进行交换，那么跳出循环。

实现

public class BubbleSort {
     //双for循环 冒泡 O(n^2)
     public static int[] bubbleSort(int[] array){
         //定义临时交换变量
        int temp;
         //排序
         for(int i= 0;i<array.length-1;i++){
             for(int j = 0;j < array.length-1-i;j++){
                 if(array[j] > array[j+1]){
                     temp = array[j];
                     array[j] = array[j+1];
                     array[j+1] = temp;
                 }
             }
         }
         return array;
     }

     //利用标记 位置记录 优化后的冒泡排序
     public static int[] optBubbleSort(int[] array){
         //标记
         boolean flag;
         //位置记录
          int tempPosition = 0;
         int len = array.length-1;
         //临时交换变量
         int temp;
         //排序
         for(int i= 0;i<array.length-1;i++){
             flag = true;
             for(int j = 0;j < len;j++){
                 if(array[j] > array[j+1]){
                     temp = array[j];
                     array[j] = array[j+1];
                     array[j+1] = temp;
                     flag = false;
                     tempPosition = j;  //记录交换的位置
                 }
             }
             if (flag){
                 return array;
             }
             len = tempPosition;
         }
         return array;
     }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        int[] arrays1 = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(bubbleSort(arrays)));
        System.out.println(Arrays.toString(optBubbleSort(arrays1)));
    }
}

快速排序

思想

排序思路：冒泡的改进版，采用递归的思想，在待排序的n个元素中任取一个元素（通常取第一个元素）作为基准，把该元素放入适当位置后，数据序列被此元素划分成两部分。所有关键字比改元素关键字小的放在基准的前面，比它大的放在基准的后面，然后基准放在中间位置，这就是一次排序。之后对前后两个部分分别重复上述过程，直至每部分内只有一个元素或没有元素为止。
说明：每趟产生的有序区一定是全局有序区，因为每趟都能把一个元素归位。

实现

public class QuickSort {
 
     public static int[] RecursionQuickSort(int left,int right,int[] array) {
         if(array == null || array.length == 0){
             return array;
         }
         //定义变量  左哨兵l 右哨兵r 基准base 临时变量temp
         int l, r, base, temp;
         if (left > right) {
             return array;
         }
         base = array[left];
         l = left;
         r = right;
         while (l != r) {
             //哨兵r从右向左找小于基准base的值
             while (array[r] >= base && l < r)
                 r--;
             //哨兵l从左向右找小于基准base的值
             while (array[l] <= base && l < r)
                 l++;
             //交换两哨兵找到的值
             if (l < r){
                 temp = array[l];
                 array[l] = array[r];
                 array[r] = temp;
             }
         }
         //将基准数归位  交换哨兵array[l]与array[left]的值
         array[left] = array[l];
         array[l] = base;
         //递归调用
         RecursionQuickSort(left,l-1,array);
         RecursionQuickSort(l+1,right,array);
         return array;
   }
   
   public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(RecursionQuickSort(0,arrays.length-1,arrays)));
   }
}

归并排序

思想

排序思路：将1个长度为n的待排序列划分为n个长度为1的序列，然后进行两两归并，得到n/2个长度为2的有序序列，再进行两两归并，一直到得到一个长度为n的有序序列。
说明：每趟产生的有序区只是局部有序区。

实现

public class MergeSort {
    //分治
    public static int[] mergeSort(int[] array,int left,int right){
        //数组内只有一个数则不用排序
        if(left >= right){
            return array;
        }
        //将大数组分为两个小数组
         int mid = (left + right) / 2;
        //左边小数组排序
        array = mergeSort(array,left,mid);
        //右边小数组排序
        array = mergeSort(array,mid+1,right);
        //合并数组
        merge(array, left, mid, right);

        return array;
    }

    //归并
    public static void merge(int[] array, int left, int gap, int right){
        //临时合并数组
        int[] arr = new int[array.length];
        //左右指针
        int leftIndex = left;
        int rightIndex = gap+1;
        //遍历数组
        int i = 0;
        //
        while (leftIndex <= gap && rightIndex <= right){
            if(array[leftIndex] < array[rightIndex] ){
                arr[i++] = array[leftIndex++];
            }else {
                arr[i++] = array[rightIndex++];
            }
        }
        //右边已排完序 将左边挪至新数组
        while (leftIndex <= gap){
            arr[i++] = array[leftIndex++];
        }
        //左边已排完序 将右边挪至新数组
        while (rightIndex <= right){
            arr[i++] = array[rightIndex++];
        }
        // 把临时数组复制到原数组
        for (int j = 0; j < i; j++) {
            array[left++] = arr[j];
        }
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        System.out.println(Arrays.toString(mergeSort(arrays,0,arrays.length-1)));
    }
}

基数排序

思想

基数排序有两种：最低位优先（LSD）和最高位优先（MSD）
排序思路：最低位优先的过程是先按最低位的值对元素进行排序，在此基础上再按次低位进行排序，依此类推。由低位向高位，每趟都是根据关键字的一位并在前一趟的基础上对所有元素进行排序，直到最高位。
最高位优先则与此相反
说明：基数排序每趟并不产生有序区，只有最后一次排序完成后整个序列才是有序的。

实现

public class BaseSort {

    public int[] sort(int[] sourceArray) {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
        int maxDigit = getMaxDigit(arr);
        return radixSort(arr, maxDigit);
    }

    //获取最高位数
    private int getMaxDigit(int[] arr) {
        int maxValue = getMaxValue(arr);
        return getNumLenght(maxValue);
    }

    private int getMaxValue(int[] arr) {
        int maxValue = arr[0];
        for (int value : arr) {
            if (maxValue < value) {
                maxValue = value;
            }
        }
        return maxValue;
    }

    protected int getNumLenght(long num) {
        if (num == 0) {
            return 1;
        }
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) {
            lenght++;
        }
        return lenght;
    }

    private int[] radixSort(int[] arr, int maxDigit) {
        int mod = 10;
        int dev = 1;
        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
            //考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数(bucket + 10)
            int[][] counter = new int[mod * 2][0];
            for (int item : arr) {
                int bucket = ((item % mod) / dev) + mod;
                counter[bucket] = arrayAppend(counter[bucket], item);
            }
            int pos = 0;
            for (int[] bucket : counter) {
                for (int value : bucket) {
                    arr[pos++] = value;
                }
            }
        }
        return arr;
    }

    //自动扩容，并保存数据
    private int[] arrayAppend(int[] arr, int value) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    }

    public static void main(String[] args) {
        int[] arrays = {8,4,6,1,5,3,9,2,7,0};
        BaseSort baseSort = new BaseSort();
        System.out.println(Arrays.toString(baseSort.sort(arrays)));
    }
}