hdu5875 - Function（线段树 暴力）ICPC网络赛大连赛区

题目链接

关于线段树的一道题
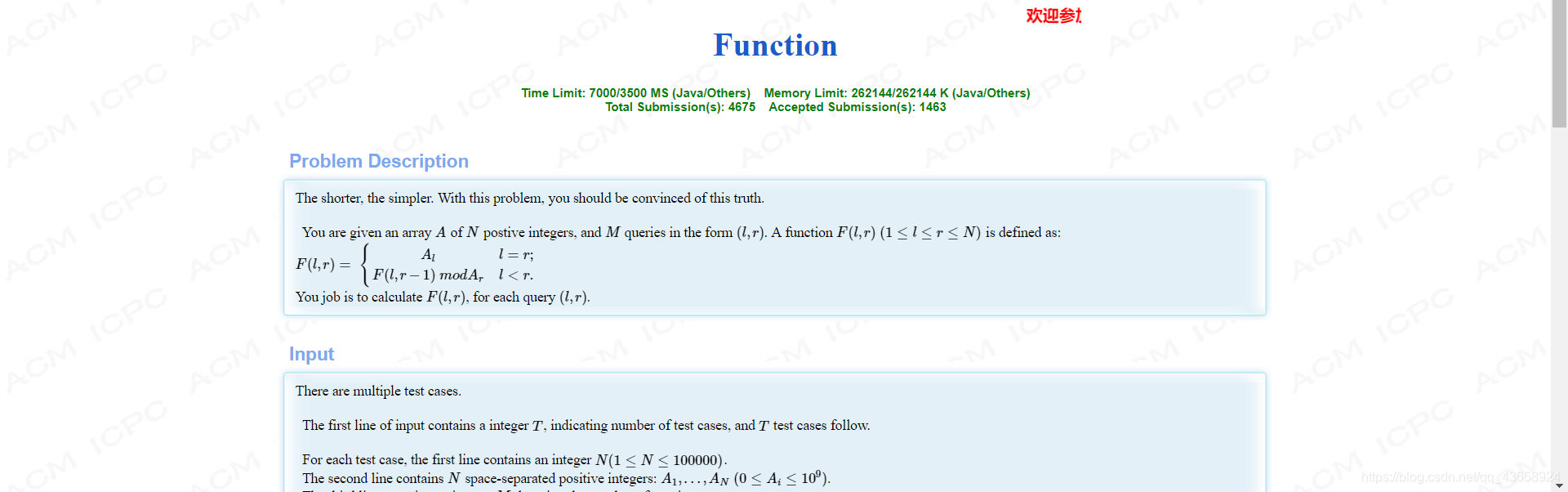
主要考察建树、更新、查询和最后输出的操作
F（l,r）分解后就是-
A(l) % A(l+1) % A(l+2) %…% A(r-1) % A®
分解后会发现最后的取值只与 A(l)和 >=A(l)的数值有关
这题对树的维护比较麻烦

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn =0x3f3f3f3f;

struct node
{
    int r,l,mmin;  //l,r分别表示线段区间左右端点
}tree[400010];

int a[100000];
void buildtree(int node,int b,int e)
{
    int mid =(b+e)/2;
    tree[node].l=b;
    tree[node].r=e;
    tree[node].mmin = maxn;
    if(b==e) return;
    if(b<=mid)
        buildtree(node*2,b,mid);  //左右同时进行建树，进行初始化
    if(e>mid)
        buildtree(node*2+1,mid+1,e);
}

void update(int node,int b,int e,int add)
{
    if(tree[node].l>=b&&tree[node].r<=e) {tree[node].mmin=add;return;}
    int mid=(tree[node].l+tree[node].r)/2;
    if(b<=mid)
        update(node*2,b,e,add);
    if(mid<e)
        update(node*2+1,b,e,add);
    tree[node].mmin=min(tree[node*2].mmin,tree[node*2+1].mmin);
}

int query(int node,int ql,int qr,int x)
{
    if(tree[node].l==tree[node].r)
    {
        if(tree[node].mmin<=x)
            return tree[node].l;
        else return -1;
    }

    int mid=(tree[node].l+tree[node].r)/2;

    //先看左儿子中最小值是否小于x
    if(mid>=ql && tree[node*2].mmin<=x)
    {
        int temp=query(node*2,ql,qr,x);
        if(temp!=-1)
            return temp;
        //在左儿子中没找到这个最小值那一定在右儿子里面
        else if(mid <qr && tree[node*2+1].mmin<=x)
            return query(node*2+1,ql,qr,x);
    }
    //左儿子的最小值不小于x并且右儿子最小值小于x那一定在右儿子里
    else if(mid<qr && tree[node*2+1].mmin<=x)
    {
        return query(node*2+1,ql,qr,x);
    }
    //左右区间都没有比x小的
    return -1;
}


int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        buildtree(1,1,n);
        for(int i=1;i<=n;++i)
        {
            scanf("%d",&a[i]);
            update(1,i,i,a[i]);
        }

        int m;
        scanf("%d",&m);
        while(m--)
        {
            int ql,qr;
            scanf("%d%d",&ql,&qr);
            int x=a[ql];
            while(ql<qr)
            {
                ql=query(1,ql+1,qr,x);//从下一个开始
                if(ql==-1)//找不到比x更小的了（已经找到答案了）
                    break;
                x%=a[ql];
            }
            printf("%d\n",x);
        }
    }
    return 0;
}