机器学习数学基础

什么是机器学习

对于某给定的任务T，在合理的性能度量方案P的前提下，某计算机程序可以自主学习任务T的经验E。随着提供合适、优质、大量的经验E，该程序对于任务T的性能逐步提高。
即:随着任务的不断执行,经验的累积会带来计算机性能的提升。

机器学习的对象:
1、一个或者多个任务 Task——T
2、经验 Experience——E
3、性能 Performance——P

机器学习可以解决什么
1、给定数据的预测问题
2、数据清洗/特征选择
3、确定算法模型/参数优化
4、结果预测

机器学习不能解决什么
1、大数据存储/并行计算
2、做一个机器人

机器学习的一般流程
数据收集–数据清洗–特征工程–数据建模–模型预测

机器学习的角度看数学

数学分析

导数与梯度

简单的说，导数就是曲线的斜率，是曲线变化快慢的反应。根据求导公式得到函数$f(x)=Inx$的导数后，进一步根据换底公式、反函数求导等，得到其他初等函数的导数。


1、凸函数
二阶导数是斜率变化快慢的反应，表征曲线凸凹性。二阶导数连续的曲线，往往称之为“光顺”的。

凸函数举例：

2、一阶可微

3、二阶可微

4、方向导数

5、梯度

泰勒展开式

泰勒展开式的应用
数值计算：初等函数值的计算(在原点展开)
在实践中，往往需要做一定程度的变换。

概率论

古典概型

概率公式

概率统计量

1、事件的独立性

2、期望

期望的性质

3、方差

方差的性质

4、协方差

协方差的性质


协方差和独立、不相关

协方差的意义

5、协方差矩阵

6、相关系数

常见概率分布

Beta分布

Beta分布的期望：

Sigmoid/Logistic函数

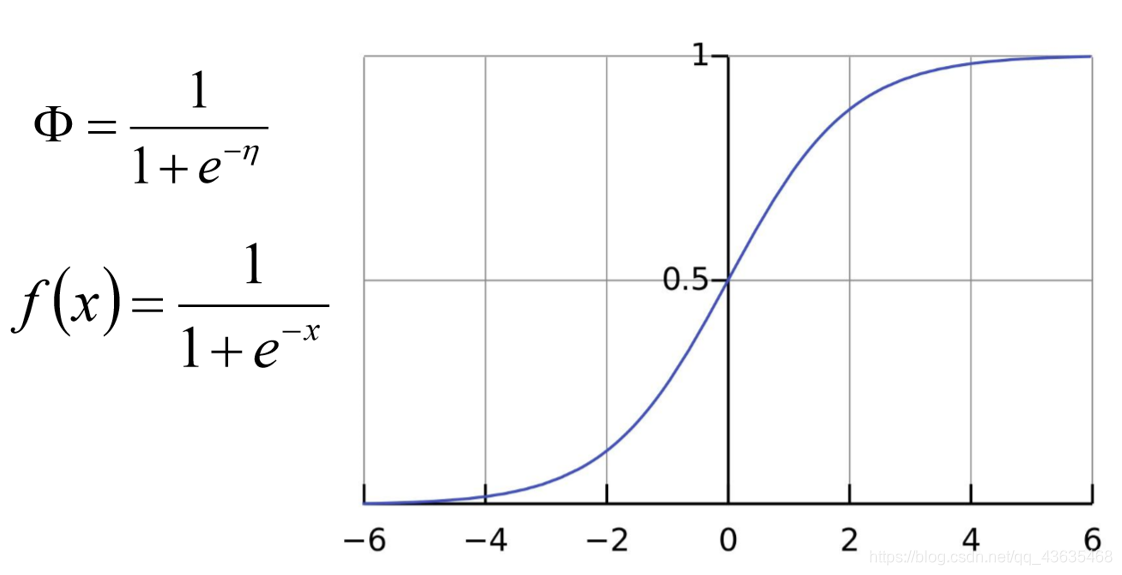
Sigmoid函数的导数

切比雪夫不等式

大数定律

大数定律的意义

中心极限定理

中心极限定理的意义

最大似然估计

线性代数

矩阵

1、行列式


2、代数余子式

3、伴随矩阵

4、方阵的逆

5、范德蒙行列式

6、矩阵乘法

7、矩阵和向量的乘法

8、矩阵的秩


9、向量组的等价

10、正交阵

特征值和特征向量

特征值的性质

特征向量的性质



正定阵

正定阵的判定

矩阵求导

1、向量的导数

2、标量对向量的导数

3、标量对方阵的导数