机器学习（八）：DBSCAN算法（基础篇）

机器学习（八）：DBSCAN算法（基础篇）

  K-Means算法和 Mean Shift算法都是基于距离的聚类算法，基于距离的聚类算法的聚类结果是球状的簇，当数据集中的聚类结果是非球状结构时，基于距离的聚类算法的聚类效果并不好。

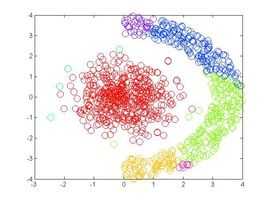
与基于距离的聚类算法不同的是，基于密度的聚类算法可以发现任意形状的聚类。在基于密度的聚类算法中，通过在数据集中寻找被低密度区域分离的高密度区域，将分离出的高密度区域作为一个独立的类别。

密度聚类

  密度聚类也被称作“基于密度的聚类”（density-based clustering），此算法假设聚类结构能通过样本分布的紧密程度确定，通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类以获取最终的聚类结果。

DBSCAN算法

 DBSCAN算法是一种著名的聚类算法，它基于一组“邻域”（neighborhood)参数来刻画样本分布的紧密程度。想要了解DBSCAN算法，DBSCAN是一种很典型的密度聚类算法，和K-Means，BIRCH这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。首先需要知道下面几个概念：

给定数据集$D={x_1,x_2,…,x_m} $:,则：

• $ϵ$-邻域：对$x_i\in D$，其$\in$-邻域包含样本集D中于$x_j$不大于$ϵ$的样本，即 N ϵ ( x j ) = { x i ∈ D ∣ d i s t ( x i , x j ) ≤ ϵ } N_{\epsilon}(x_j)=\{x_i\in D|dist(x_i, x_j )\le \epsilon\} Nϵ​(xj​)={ xi​∈D∣dist(xi​,xj​)≤ϵ} 其中，dist()默认情况下为欧式距离。（可以将邻域理解为一个圆，圆内包含着一定数量的样本）
• 核心对象：若$x_j$的$ϵ$-邻域至少包含$MinPts$个样本，即$|N_{ϵ}|\ge MinPts$,则$x_j$是一个核心对象。(简单理解就是：圆的中心(即核心对象)周围必须超过MinPts个样本。）
• 密度直达：若$x_j$位于$x_i$的$ϵ$-邻域中，且$x_i$是核心对象，则称 x j x_j