机器学习day1

batch梯度下降算法

假设有训练数据

这是42个房屋的数据，包括房子大小以及房屋价格
我们的假设满足数据的函数是这样的线性函数Hypothesis:$h\theta (x)=\theta 0+\theta 1x$
$\theta i:模型参数$
$\theta 取不同的值有不同的模型$

我们因该选取最佳的$\theta$like this尽量拟合数据:

为了求出最适合的$\theta$我定义一个代价函数

$J(\theta 0,\theta 1)=\frac{1}{2m}{\sum }_{i=0}^M(h_{\theta }(x^i)-y^i{)}^2$
minimize$J(\theta 0,\theta 1)$
我们将使用梯度下降算法minimize$J(\theta 0,\theta 1)$，以及得到相应的$\theta$
这是梯度下降算法的工作图，我们随机挑选一个点，不断改变$\theta$，使代价函数最小化或局部最小
这是初始点

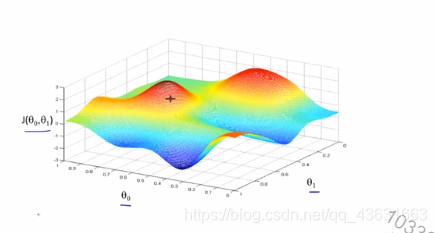
工作过程

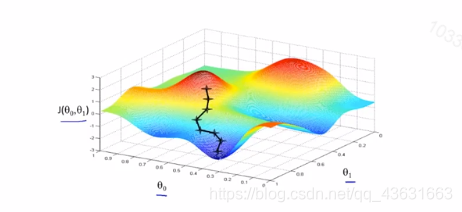
或初始化令一个随机点like this

这样我们就得到了最小化代价函数的$\theta$
这是其背后的数学公式：
${\Theta }_j:={\Theta }_j-\alpha \frac{\partial J(\theta 0,\theta 1)}{\partial {\Theta }_j}$(这里j=0或1)
不断的重复更新$\theta$like this这是带进去之后的结果