树和二叉树——二叉树遍历与构建_树的遍历,每个结点都两次-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43627109/article/details/103137655

1、二叉树的遍历
二叉树的遍历是指从根结点出发，按照某种次序访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次。
属于抽象操作，可以是对结点进行的各种处理，这里简化为输出结点的数据。
包括前序遍历、中序遍历、后序遍历、层序遍历。
遍历操作的目的：非线性结构线性化

前序（根）遍历
若二叉树为空，则空操作返回；否则：
①访问根结点；
②前序遍历根结点的左子树；
③前序遍历根结点的右子树。
中序（根）遍历
若二叉树为空，则空操作返回；否则：
①中序遍历根结点的左子树；
②访问根结点；
③中序遍历根结点的右子树。
后序（根）遍历
若二叉树为空，则空操作返回；否则：
①后序遍历根结点的左子树；
②后序遍历根结点的右子树。
③访问根结点；
层序遍历
二叉树的层次遍历是指从二叉树的第一层（即根结点）开始，从上至下逐层遍历，在同一层中，则按从左到右的顺序对结点逐个访问。
2、二叉树的存储–顺序存储
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置（下标）应能体现结点之间的逻辑关系——父子关系。
二叉树的顺序存储结构一般仅存储完全二叉树
前序

void Preorder(int root, char data[]){
	if(data[root]!='\0'){
		cout<<data[root] ;			
		Preorder(2*root,data);
		Preorder(2*root+1,data);

	}
	return;
}

中序

void InOrder(int root, char data[]){
	if(data[root]!='\0'){
		InOrder(2*root,data);
		cout<<data[root] ;			
		 InOrder(2*root+1,data);	
	}
	return;
}

后序

void PostOrder(int root, char data[]){
	if(data[root]!='\0'){
		 PostOrder(2*root,data);
		 PostOrder(2*root+1,data);
		cout<<data[root] ;			
	}
	return;
}

void create(char preorder[],char inorder[],int start_p, int end_p,int start_i,int end_i, char data[],int root){
	if(start_p>end_p)
		return ;
	else{
		int k;
		for(int i=start_i;i<=end_i;i++){
			if(inorder[i]==preorder[start_p]){
				k=i;
				break;
			}
		}
		data[root]=preorder[start_p];
		create(preorder,inorder,start_p+1,start_p+k-start_i,start_i,k-1,data, 2*root);
		create(preorder,inorder,start_p+k-start_i+1,end_p,k+1,end_i,data,2*root+1);
	}
	return ;
}
int main(){   
    char * data;
	int total=1;
	char preorder[100],inorder[100];
	cin>>preorder>>inorder;
	int length=0;
	while(preorder[length]!='\0')
		length++;
	data=new char[pow(2,length+1)];
	memset(data,'\0',pow(2,length+1));
	create(preorder,inorder,0,length-1,0,length-1,data,1);
	order(1,data);
	return 0;
}

3、二叉树的存储–二叉链表
基本思想：令二叉树的每个结点对应一个链表结点，链表结点除了存放与二叉树结点有关的数据信息外，还要设置指示左右孩子的指针。
在这里插入图片描述

template <class T>
struct BiNode
{
    T data;
    BiNode<T> *lchild, *rchild;
};

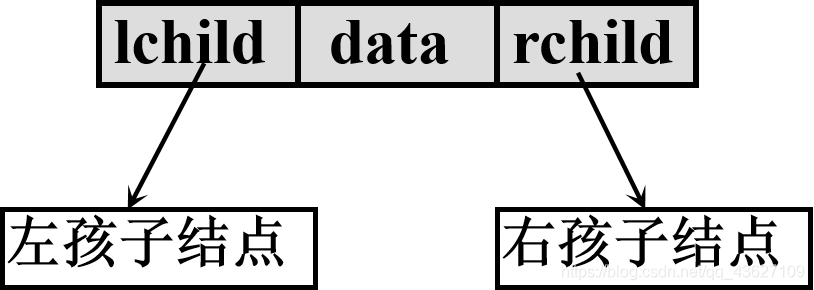
在这里插入图片描述
具有n个结点的二叉链表中，有n+1个空指针。
4、具体实现

声明

template <class T>
class BiTree
{    
  public:
       BiTree(); 
        ~BiTree( );            
        void PreOrder(){PreOrder(root);} 
        void InOrder() {InOrder(root);} 
        void PostOrder() {PostOrder(root);} 
        void LevelOrder(){LeverOrder(root)};
  private:
        BiNode<T> *root; 
        BiNode<T> * Creat( ); 
        void Release(BiNode<T> *root);
        void PreOrder(BiNode<T> *root); 
        void InOrder(BiNode<T> *root); 
        void PostOrder(BiNode<T> *root); 
        void LevelOrder(BiNode<T> *root);
 };

前序遍历–递归算法

template   <class T>
void   BiTree::PreOrder(BiNode<T> *root) 
{
        if (root ==NULL)  return;     
        else {
            cout<<root->data;         
            PreOrder(root->lchild);    
            PreOrder(root->rchild);    
        }
 }

前序遍历–非递归算法
二叉树前序遍历的非递归算法的关键：
在前序遍历过某结点的整个左子树后，如何找到该结点的右子树的根指针。
解决办法：在访问完该结点后，将该结点的指针保存在栈中，以便以后能通过它找到该结点的右子树。
思想：
遇到一个结点，就访问该结点，并把此结点推入栈中，然后遍历它的左子树；遍历完它的左子树后，从栈顶托出这个结点，并按照它的右链接指示的地址再去遍历该结点的右子树结构。

伪代码：
1.栈s初始化（空栈）；
2.循环直到root为空且栈s为空 
　2.1 当root不空时循环
　　2.1.1 输出root->data;
    　2.1.2 将指针root的值保存到栈中；
    　2.1.3 继续遍历root的左子树（root=root->lchild）
　2.2 如果栈s不空，则
　　2.2.1 将栈顶元素弹出至root（root=s.pop()）；
　　2.2.2 准备遍历root的右子树(root=root->rchild)；

template <class T>
void BiTree::PreOrder(BiNode<T> *root) {
  SeqStack<BiNode<T> *>  s;
     while (root!=NULL | | !s.empty()) {
         while (root!= NULL)  {
             cout<<root->data;
             s.push（root）;
             root=root->lchild;  
         }
         if (!s.empty()) { 
             root=s.pop();
             root=root->rchild;  
         }
     }
}

中序遍历–递归算法

template <class T>
void BiTree::InOrder (BiNode<T> *root)
{
         if (root==NULL) return;     
         else {
               InOrder(root->lchild); 
               cout<<root->data; 
               InOrder(root->rchild);
         }
}

中序遍历–非递归算法
思想：
遇到一个结点，就把它推入栈中，并去遍历它的左子树
遍历完左子树后，从栈顶托出这个结点并访问之，然后按照它的右链接指示的地址再去遍历该结点的右子树。

伪代码：
1.栈s初始化（空栈）；
2.循环直到root为空且栈s为空 
　2.1 当root不空时循环
        2.1.1 将指针root的值保存到栈中；
    　2.1.2 继续遍历root的左子树（root=root->lchild）
　2.2 如果栈s不空，则
　　2.2.1 将栈顶元素弹出至root（root=s.pop()）；
 　　  2.2.2 输出root->data;
　　2.2.3 准备遍历root的右子树(root=root->rchild)；

template <class T>
void BiTree::InOrderwithoutD (BiNode<T> *root)
	 {
     	stack< BiNode<T> * > aStack;

while(!aStack.empty()||root) {
	while(root){
    aStack.push(root);
    root=root->lchild; 	 
    }
    if(!aStack.empty()){
		  root=aStack.top();				
		  aStack.pop(); 
          cout<<root->data;
           root=root->rchild; 
  }
}

后序遍历–递归算法

template <class T>
void BiTree::PostOrder(BiNode<T> *root)
{ 
    if (root==NULL) return; 
    else {
         PostOrder(root->lchild); 
         PostOrder(root->rchild); 
         cout<<root->data;          
    }
}

后序遍历–非递归算法
思想:
遇到一个结点，把它推入栈中，遍历它的左子树
左子树遍历结束后，还不能马上访问处于栈顶的该结点，而是要再按照它的右链接结构指示的地址去遍历该结点的右子树
遍历遍右子树后才能从栈顶托出该结点并访问之。
解决方案：
需要给栈中的每个元素加上一个特征位，以便当从栈顶弹出一个结点时区别是从栈顶元素左边回来的(则要继续遍历右子树)，还是从右边回来的(该结点的左、右子树均已遍历)
特征为Left表示已进入该结点的左子树，将从左边回来；特征为Right表示已进入该结点的右子树，将从右边回来

算法分析
定义一个栈；从根节点出发开始遍历，p=root，如果，root==NULL, 不进行遍历；
无条件进行下面的工作
①如果指针不空，指针打上left标记，并将指针进栈，执行②;否则，执行③
②p=p->lchild,重复①
③栈顶元素出栈P
④查看P的标志，如果标志为right,进行下面的工作，否则，执行⑤
a)访问当前节点P
b)如果栈空 ，算法结束；
c)否则，栈顶元素出栈，转④
⑤修改P的标志，让P重新入栈，p=P->rchild,执行2

栈中的元素类型定义StackElement
 	enum Tags{Left,Right};	//特征标识定义
	template <class T>
	class StackElement		//栈元素的定义
	{
	public:
	BiTreeNode<T>* pointer;     //指向二叉树结点的指针
	Tags tag; //特征标识申明
	};

#include <stack>
using namespace std;
template<class T>
void BiTree<T>::PostOrderWithoutRecusion(BiTreeNode<T>* root){
	StackElement<T> element;
	stack<StackElement<T > > aStack;//栈申明
	BiTreeNode<T>* pointer;
	if(root==NULL)
		return;//空树即返回
	else    
		pointer=root;				
	while(true){
		while(pointer!=NULL){//进入左子树
			element.pointer=pointer;
			element.tag=Left; //沿左子树方向向下周游
			aStack.push(element);
			pointer=pointer->lchild; 	
		}
   		element=aStack.pop();
        pointer=element.pointer; 
	    while(element.tag==Right){
	        cout<<pointer->data;
	        if(aStack.empty())  return;
		    else{
		       element=aStack.pop();
			   pointer=element.pointer;
	  	 }//end else
        } //endwhile
	element.tag=Right; 
    aStack.push(element);
    pointer=pointer->rchild(); 
     }//end while
}

层序遍历

1.队列Q初始化；
2. 如果二叉树非空，将根指针入队；
3.  循环直到队列Q为空
      3.1 q=队列Q的队头元素出队；
      3.2 访问结点q的数据域；
      3.3 若结点q存在左孩子，则将左孩子指针入队；
      3.4 若结点q存在右孩子，则将右孩子指针入队；

#include <queue>
using namespace std;
template<class T>
void BiTree<T>::LevelOrder(BinaryTreeNode<T>* root){
	queue<BiTreeNode<T>*> aQueue;
	if(root)
		aQueue.push(root);
	while(!aQueue.empty())
		{
		root=aQueue.front(); //取队列首结点
	 	aQueue.pop();
                     cout<<pointer->data;//访问当前结点
		if(root->lchild)	//左子树进队列
			aQueue.push(root->lchild);
		if(root->rchild) //右子树进队列
			aQueue.push(root->rchild); 	
	}//end while
}

析构

template<class T>
BiTree<T>::~BiTree(void)
{
	Release(root);
}

template<class T>
void BiTree<T>::Release(BiNode<T>* root){
  if (root != NULL){                  
      Release(root->lchild);   //释放左子树
      Release(root->rchild);   //释放右子树
      delete root;
  }  
}

5、遍历小结
都是沿着左分支访问，直到左分支为空时，再依次对栈中节点的右分支进行处理。（遵循从左至右的遍历原则，体现深度优先搜索的思想）
前序遍历：每个节点只进栈一次，在进栈前访问节点
中序遍历：每个节点进栈一次，在出栈时访问节点
后序遍历：每个节点进栈两次，在第二次出栈时访问节点
5、二叉树的建立
由遍历序列完成二叉树的构建：为了建立一棵二叉树，将二叉树中每个结点的空指针引出一个虚结点，其值为一特定值如“#”，以标识其为空，把这样处理后的二叉树称为原二叉树的扩展二叉树。
二叉树的建立：
设二叉树中的结点均为一个字符。假设扩展二叉树的前序遍历序列由键盘输入，root为指向根结点的指针，二叉链表的建立过程是：
①按扩展前序遍历序列输入结点的值
②如果输入结点值为“#”,则建立一棵空的子树
③否则，根结点申请空间，将输入值写入数据域中，
④以相同方法的创建根结点的左子树
⑤以相同的方法创建根结点的右子树
递归方法

template <class T>
BiTree ::BiTree(){ 
      root=creat()；
}

template <class T>
BiNode<T> * BiTree ::Creat(){
     BiNode<T> *root; char ch;
    cin>>ch;
    if (ch=='# ')     root=NULL; 
    else {
        root=new BiNode<T>; 
        root->data=ch;
        root->lchild=creat(); 
        root->rchild= creat(); 
    }  
  return root
}

声明：

template <class T>
class BiTree{
public:
       BiTree(); 
        ~BiTree( );            
        void PreOrder(){PreOrder(root);} 
        void InOrder() {InOrder(root);} 
        void PostOrder() {PostOrder(root);} 
        void LevelOrder();
  private:
        BiNode<T> *root; 
        void Creat(BiNode<T> *& root); 
        void Release(BiNode<T> *root);
        void PreOrder(BiNode<T> *root); 
        void InOrder(BiNode<T> *root); 
        void PostOrder(BiNode<T> *root); 
        void LevelOrder(BiNode<T> *root);
};

template <class T>
void BiTree<T>::Creat(BiNode<T> * &root  )
{
	    T ch;
	    cout<<"请输入创建一棵二叉树的结点数据"<<endl;
	    cin>>ch;
         if (ch=="#") root = NULL;
         else{ 
	           root = new BiNode<T>;       //生成一个结点
                root->data=ch;
               Creat(root->lchild );    //递归建立左子树
               Creat(root->rchild);    //递归建立右子树
    } 
}