Treap 平衡二叉查找树

【基本概念】
Treap=Tree+Heap。Tree是指二叉搜索树，而Heap指的是二叉堆，一般是最小堆。Treap需要维护两值，一个是二

叉搜索树中的键值（key），另一个是最小堆中的优先级（aux）。Treap是一棵aux值满足最小堆性质的二叉树。

Treap的aux值是在插入时随机赋值的。所以会出现新插入的节点不满足堆的性质，所以需要引入旋转操作。

如下图所示：

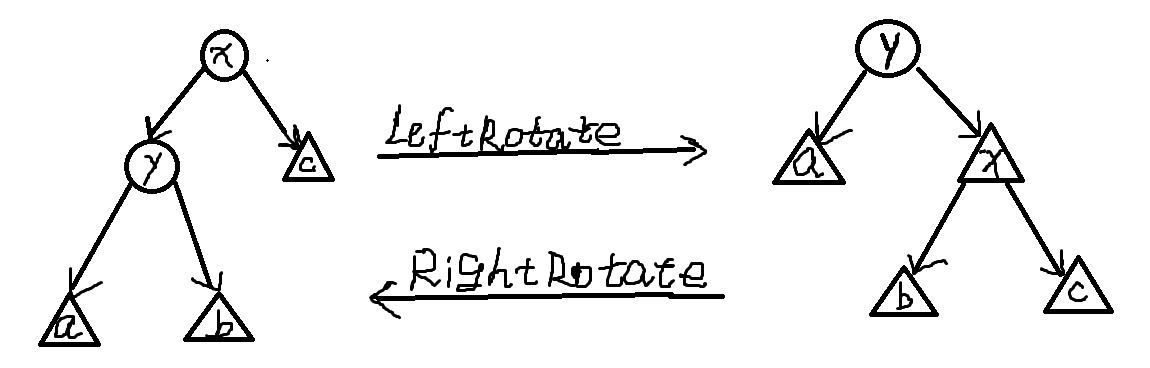
图中圆圈表示单个节点，而三角形表示一个子树，子树可以为空树。

容易发现，旋转操作不会影响到Treap的二叉搜索树的性质。所以当不满足堆性质时，可以通过旋转操作来使它满

足堆性质。

右旋操作：

void zig(int &p)
{
    int q=a[p].l;
    a[p].r=a[q].l;
    a[q].r=p;
    p=q;  //p这里是引用
}

左旋操作：

void zag(int &p)
{
    int q=a[p].r;
    a[p].l=a[q].r;
    a[q].l=p;
    p=q;  //p这里是引用
}

左旋一个子树，会把它的根节点旋转到根的左子树位置，同时根节点的右子节点成为子树的根
右旋一个子树，会把它的根节点旋转到根的右子树位置，同时根节点的左子节点成为子树的根
如图666所示，我们可以从图中清晰地看出左旋后的根节点降到了左子树，右旋后根节点降到了右子树
而且仍然满足BSTBSTBST性质，于是有：
旋转的性质2
对子树旋转后，子树仍然满足BST性质。

利用旋转的两条重要性质
我们可以来改变树的结构
实际上我们恰恰是通过旋转使Treap节点之间满足堆序。
如图777所示的左边的一个Treap，它仍然满足BSTBSTBST性质，但是由于某些原因，节点4和节点2之间不满足最小堆序，4作为2的父节点，它的修正值大于左子节点的修正值
我们只有将2变成4的父节点，才能维护堆序
根据旋转的性质我们可以知道，由于2是4的左子节点，为了使2成为4的父节点，我们需要把以4为根的子树右旋
右旋后，2成为了4的父节点，满足堆序。

 

【性质】

可以证明，优先级值随机赋值，可以使Treap的期望深度为O（logN）。

【算法】

1.查找和普通的二叉搜索树相同。

2.插入的时候，需要判断插入后是否符合堆的性质，不符合则需要一直旋转，直到满足堆性质。

算法：Treap的插入Insert（T，x）。

具体流程：

1.如果T是空树，将T变成一个只含有一个节点x的二叉搜索树

2.如果T的根节点的值为x,属于重复值，返回

3.如果x少于T的根节点的值

（3.1）Insert(T的左子树，x)

（3.2）如果T的左儿子不满足堆性质(即优先级比T的小)，则LeftRotate(T)

4.否则

（4.1）Insert(T的右子树，x)

（4,2）如果T的右子树不满足堆的性质，则RightRotate(T)

3，删除操作在引入了旋转操作后显得更直观。只需要将待删除节点在保证其他节点堆性质的情况下，将其旋转成叶子节点即可。

算法：Delete（T），删除树T的根节点

输入：节点T

具体流程：

（1）如果T有左儿子或右儿子，做如下过程

（1.1）如果T没有右儿子，T <- LeftRotate（T）

（1.2）否则如果T没有左儿子，T <- RightRotate(T)

（1.3）否则

（1.3.1）如果T的左儿子优先级小于T的右儿子，T <-LeftRotate(T)

（1.3.2）否则，T <-RightRotate(T)

（1.4）转到（1）

（2）删除节点T。