HDU 6362 oval-and-rectangle （数学）_adjusting the compensation, parallel to the coordi-优快云博客

本篇探讨了在给定椭圆的长半轴和短半轴的情况下，求顶点位于椭圆上的矩形周长的数学期望。通过解析几何原理，利用定积分求解均值，最终给出了一个精确的数学表达式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description：

Patrick Star find an oval.

The half of longer axes is on the x-axis with length aa.

The half of shorter axes is on the y-axis with length bb.

Patrick Star plan to choose a real number cc randomly from [0,b][0,b], after that, Patrick Star will get a rectangle :

1. The four vertexes of it are on the outline of the oval.

2. The two sides of it parallel to coordinate axis.

3. One of its side is y=cy=c.

Patrick Star want to know the expectations of the rectangle's perimeter.

Input

The first line contain a integer TT (no morn than 10), the following is TT test case, for each test case :

Each line contains contains two integer a, b (0<b<a<1050<b<a<105). Separated by an white space.

Output

For each test case output one line denotes the expectations of the rectangle's perimeter .

You should keep exactly 6 decimal digits and ignore the remain decimal digits.

It is guaranted that the 7-th decimal digit of answer wont be 0 or 9.

Sample Input
1
2 1
Sample Output
8.283185

题意：给出椭圆的长半轴和短半轴，求顶点在椭圆上的矩形的周长的期望。

题解：

求期望也就是求均值。

设椭圆的方程为 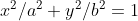$x^{2}/a^{2}+y^{2}/b^{2}=1$ ，

设矩形在第一象限的一个顶点坐标为(x,y)，则 y的范围为(0,b)，由椭圆方程可知 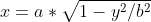$x=a*\sqrt{1-{y^{2}/{b^{2}}$ ，

所以矩形周长可表示为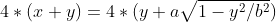 $4*(x+y)=4*(y+a\sqrt{1-y^{2}/b^{2}})$

因为要求周长的期望即均值，而定积分除以积分的区间长度就是均值

所以将周长对y积分之后再除以b即为所求。

积分过程中用到了用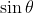 $\sin \theta$ 换元，最后的积分结果为 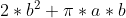$2*b^{2}+\pi *a*b$ ，再除以区间长度b即为最后结果。

需要注意的是题目要求输出6位小数，且输出的数不要求有四舍五入，可以将结果 -0.0000005来达到题目要求。

AC代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<stdlib.h>
#include<queue>
#include<map>
#include<set>
#include<iomanip>
#include<math.h>
using namespace std;
typedef long long ll;
typedef double ld;
int i,j,k;
const double PI = acos(-1.0);

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        double c = 2*b+PI*a;
        c *= 1000000;
        c = floor(c)/1000000;
        printf("%.6lf\n",c);
    }
    return 0;
}