PAT---乙级---1049 数列的片段和

最新推荐文章于 2025-01-23 21:45:00 发布

Bear in mind

最新推荐文章于 2025-01-23 21:45:00 发布

阅读量217

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_43625313/article/details/87396174

本文探讨了在处理大量数值计算时如何避免浮点数精度损失和计算效率问题，通过调整计算顺序和使用适当的类型转换，可以显著提高计算的准确性和性能。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

现在，有如下题目：
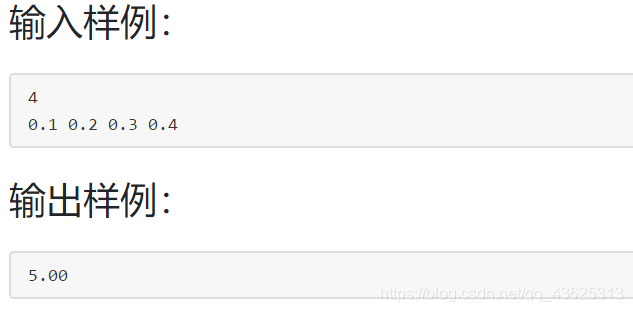
在这里插入图片描述

看到这个题目，感觉思路上很好理解，但是写起来，如果暴力的话，这样的题放在哪里都会超时。并且在大量的数累加之后浮点数就会损失精度。计算的过程越多，误差累积越大。使用浮点型进行大量计算时要尽可能地减小计算，这个时候神奇的地方就发生了：
在这里插入图片描述
从上面的描述中我们可以清楚的看到存在的规律。
sum+=a[i](n-i)(i+1)和sum=(n-i)(i+1)a[i]
在效果上是存在差异的。
前者在运算的时候都是double类型，而后者在运算时前两个是int，最后变为double
后者的写法精确度更高。但是要用long long的强制类型转换来防止溢出。
不说了，上代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
double a[100001];
int main()
{
	double sum=0;
	int n,i,j;
	cin>>n;
	for(i=0;i<n;i++)
	{
		scanf("%lf",&a[i]);
		sum+=(long long)(n-i)*(i+1)*a[i];
	}
	printf("%.2f",sum);
	return 0;
}

代码很简短，但是很巧妙，很神奇。