图的最小生成树（普里姆和克鲁斯卡尔）算法

最小生成树

文章的目录如下：

• 最小生成树的相关概念
• 普里姆算法
• 克鲁斯卡尔算法

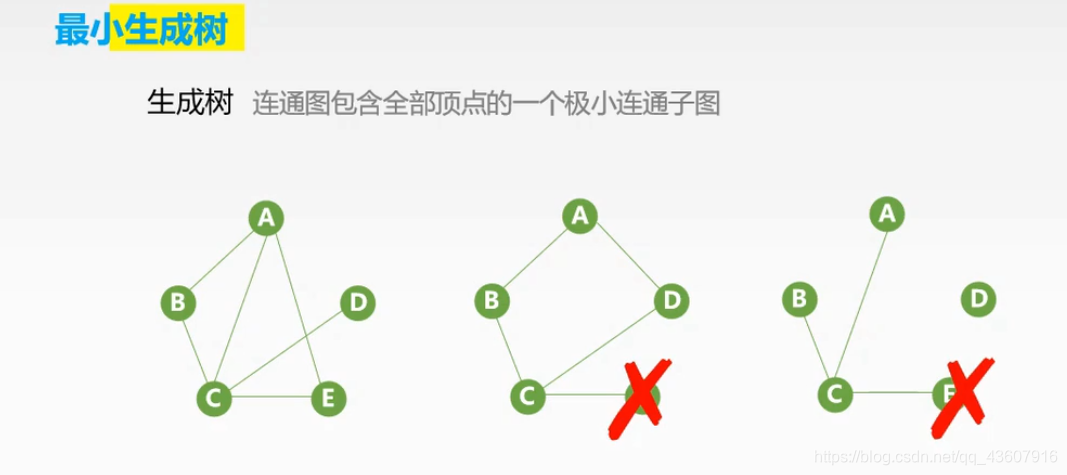
1.最小生成树

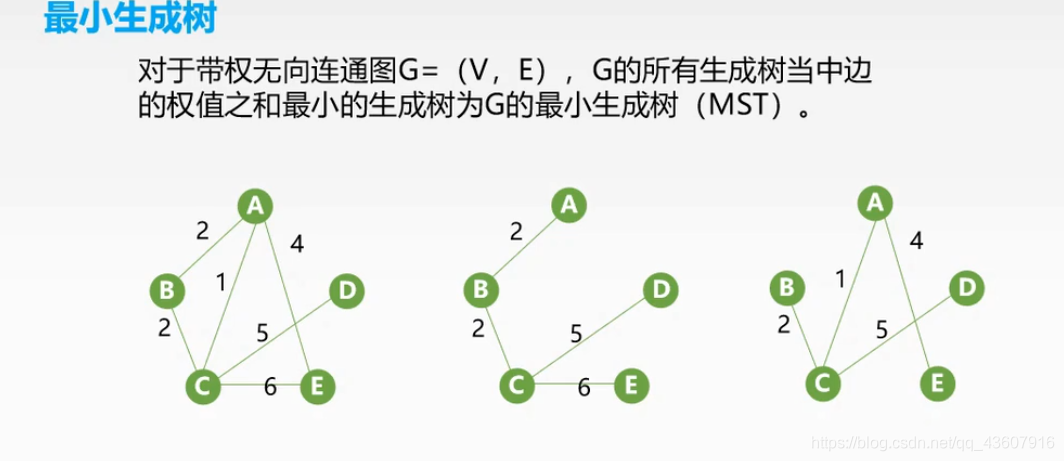
• 当最小生成树的边的权值都不等时，它是唯一的
• 当最小生成树的边的权值部分相等时，可能存在最小生成树不唯一的情况，即不一定唯一
• 当其边等于顶点数减1的时候它本身就是唯一的最小二叉树

首先要知道什么是最小生成树，这里的最小指的是图的生成树的权值之和最小，最小生成树可由以下几点的概念组成：

• 一个图的生成树集合当中权值之和最小的生成树，可以有一种，也可以有多种，这与图本身结构有关。

• 包括了图中的所有节点，所有节点之间都有边，但是没有连通图；
  就是有 N个顶点 有N-1个边；

• 就是一个连通图的极小连通子图（它包含图中的所有顶点，并且只含有尽可能少的边。），这意味着对于生成树来说，若看去他的一条边，则会使该生成树（极小连通子图）变为非连通图；同样，你多添加一条边，则图中肯定会形成一条回路。

• prim算法又称“加点法”，用于边数较多的带权无向连通图
  方法：每次找与之连线权值最小的顶点，将该点加入最小生成树集合中
  注意：相同权值任选其中一个即可，但是不允许出现闭合回路的情况。
  注意：一个图的最小生成树是不是唯一的，还得看连通图中的各边权值是不是互不相等；

   1.如果互不相等，那么连通图G的生成树肯定是唯一的；而且如果无向连通图的边数比顶点数少 （此时G本身是一棵树），此时G的最小生成树就是它本身。
   2.最小生成树的边的权值之和总是唯一的，虽然最小生成树可能不唯一（就是图形不一致），但其对应的变得权值之和总是唯一的，而且是最小的。
   3.最小生成树的边数为顶点数减1。
  

2.普里姆算法

知道了最小生成树的概念之后，我们来谈构造最小生成树的算法，一共有两种构造算法，一是普里姆算法，二是克鲁斯卡尔算法，废话不多说，下面首先来谈普里姆算法
1.算法思想
设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。
直到图中所有顶点都被并入树中为止，此时得到的生成树就是该图的最小生成树。

2.图解执行过程

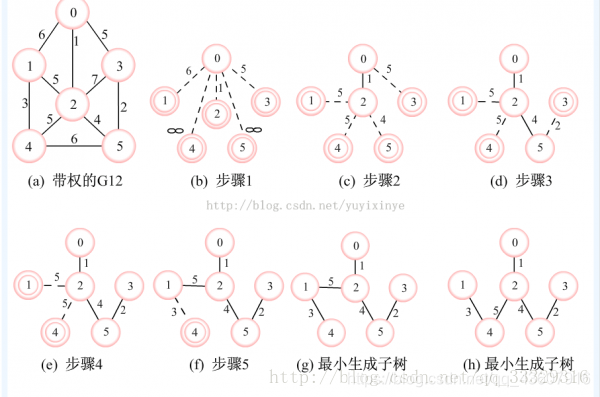
3.代码执行过程

首先需要建立两个数组vset[]和lowcost[]。vset[i]=1表示顶点i已经被并入生成树中，vset[i]=0表示顶点i未被并入生成树中，lowcost[]数组中存放当前生成树到剩余各顶点最短边的权值。
注意：“当前生成树到剩余各顶点最短边的权值”：

• 首先这句话说的是树这一整体到其余顶点的权值，而不是针对树中的某一顶点

• 当前生成树到某一顶点可能有多条边，lowcost[i]中保存的是当前生成树到顶点i的多条边中最短的一条边的权值，lowcost[]中有多个最短边的权值，最短边条数对应于剩余顶点个数，已并入生成树的边不在考虑范围内。
  执行过程：
  从树中