图论基础习题解析-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43592674/article/details/113184440

判断题
1-1
无向连通图所有顶点的度之和为偶数。T
1-2
无向连通图至少有一个顶点的度为1。F
1-3
用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。T
1-4
在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍.T
1-5
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。F
1-6
在一个有权无向图中，若b到a的最短路径距离是12，且c到b之间存在一条权为2的边，则c到a的最短路径距离一定不小于10。T
1-7
用一维数组G[]存储有4个顶点的无向图如下：

G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。T
1-8
Kruskal 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。F
1-9
Prim 算法是通过每步添加一条边及其相连的顶点到一棵树，从而逐步生成最小生成树。T
1-10
若图G有环，则G不存在拓扑排序序列。T
1-11
若图G为连通图且不存在拓扑排序序列，则图G必有环.T
1-12
P 是顶点 S 到 T 的最短路径，如果该图中的所有路径的权值都加 1，P 仍然是 S 到 T 的最短路径。
F
1-13
对于带权无向图 G = (V, E)，M 是 G 的最小生成树，则 M 中任意两点 V1 到 V2 的路径一定是它们之间的最短路径。F
1-14
如果从有向图 G 的每一点均能通过深度优先搜索遍历到所有其它顶点，那么该图一定不存在拓扑序列。T

1-15
如果 e 是有权无向图 G 唯一的一条最短边，那么边 e 一定会在该图的最小生成树上。T
选择题
2-1
在拓扑排序算法中用堆栈和用队列产生的结果会不同吗？

(1分)

A.
是的肯定不同

B.
肯定是相同的

C.
有可能会不同

D.
以上全不对
2-2
若要检查有向图中有无回路，除了可以利用拓扑排序算法外，下列哪种算法也可以用？

(2分)

A.
Dijkstra算法

B.
Prim算法

C.
广度优先搜索

D.
深度优先搜索
2-3
下图为一个AOV网，其可能的拓扑有序序列为：
在这里插入图片描述
A.
ABCDFEG

B.
ADFCEBG

C.
ACDFBEG

D.
ABDCEFG
2-4
下列选项中，不是下图深度优先搜索序列的是：
在这里插入图片描述

2-5
若将n个顶点e条弧的有向图采用邻接表存储，则拓扑排序算法的时间复杂度是：

2-6
使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：
2-7
使用迪杰斯特拉（Dijkstra）算法求下图中从顶点1到其他各顶点的最短路径，依次得到的各最短路径的目标顶点是：在这里插入图片描述
2-8
设无向图为 G=(V，E)，其中 V={v1,v2,v3,v4}，E={(v1,v2)，(v3,v4)，(v4,v1)，(v2,v3)，(v1,v3)}。则每个顶点的度依次为：

(2分)

A.
2, 1, 1, 1

B.
1, 1, 2, 1

C.
3, 2, 3, 2

D.
2, 3, 2, 3

2-9
对于给定的有向图如下，其逆邻接表为：
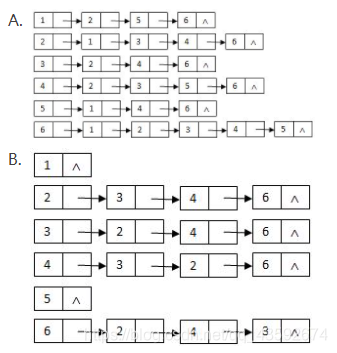
在这里插入图片描述

因为是逆连接矩阵，所以选a

2-11
给定一个图的邻接矩阵如下，则从V1出发的宽度优先遍历序列（BFS，有多种选择时小标号优先）是：
2-12
给出如下图所示的具有 7 个结点的网 G，哪个选项对应其正确的邻接矩阵？在这里插入图片描述

2-13
已知无向图 G 如下所示，使用克鲁斯卡尔（Kruskal）算法求图 G 的最小生成树，加入到最小生成树中的边依次是：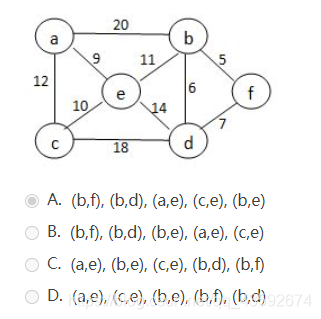
2-14
若使用 AOE 网估算工程进度，则下列叙述中正确的是：