图的拓扑排序
主要解决一个工程能否顺序进行的问题。
(1)基本概念
-
AOV网的定义:
在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网叫AOV网。 -
AOE网的定义:
在一个表示工程的带权邮有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网,称为AOE网。(AOE网中没有入边的顶点称为始点,没有出边的顶点称为终点) -
拓扑序列的定义:
设G = (V,E)是一个具有n个顶点的有向图,V中的顶点序列V1、V2…Vn,若满足从顶点Vi1到Vj有一条路径,则在顶点序列中顶点Vi必须在顶点Vj之前(不能存在回路),则V中的这个顶点序列叫拓扑序列。 -
拓扑排序的定义:
对一个有向图构造拓扑序列的过程。
(2)对AOV网拓扑排序的思路(使用邻接表)
从AOV网中选择一个入度为0的顶点输出,然后删除此顶点,并删除以此顶点为尾的弧,继续重复此步骤,直到输出全部顶点或AOV网中不存在入度为0的顶点为止。
(3)对AOV网拓扑排序的举例
下图是一个AOV网

对应的邻接表如下(in表示该下标所对应顶点的入度)

算法步骤:
- 由邻接表可以看到入度为0的顶点分别有V0、V1、V3,所以这三个顶点入栈(第2步中V3位于栈顶,先出栈)
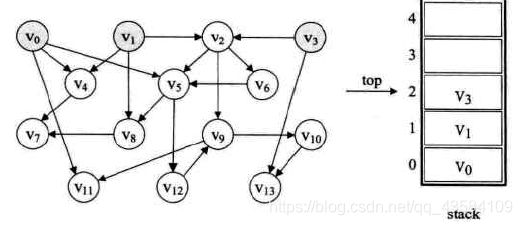
- V3出栈,输出V3,并将所有以V3为出发点的弧从网中删除(显然,V2和V13的入度会- 1)
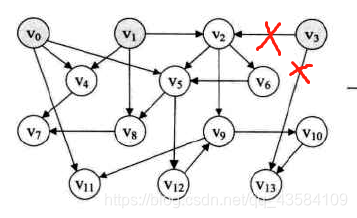
此时的输出序列: V3
- 此时,由与网中V3的去除,网中的一些顶点的入度会减小(所以有可能会有新的入度为0的顶点产生)
更新后的邻接表如下,所以栈中入度为0的顶点有V0、V1,此时V1出栈(V1位于栈顶),输出V1。并删除网所有以V1为出发点的弧(显然,V2、V4、V8的入度会 -1)
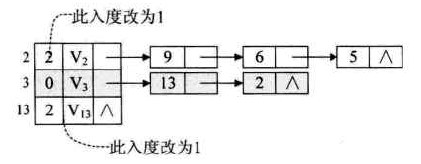
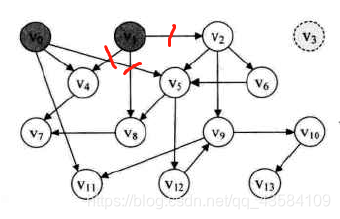
此时的输出序列: V3→V1
- 在更新邻接表后(即更新V2、V4、V8的入度),此时V2的入度为0,故V2入栈。输出V2,同时V2出栈(因为V2位于栈顶),并删除网所有以V2为出发点的弧。(V6的入度也变为0)
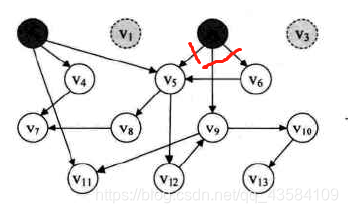
此时的输出序列: V3→V1→V2
- V6入栈。输出V6,同时V6出栈(因为V6位于栈顶),并删除网所有以V6为出发点的弧。
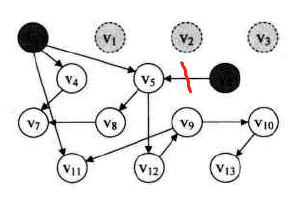
此时的输出序列: V3→V1→V2→V6
-
此时栈中只有V0了。输出V0,同时V0出栈,并删除网所有以V0为出发点的弧。(此时的 V4、V5的入度变为0,故 V4、V5进栈,拓扑序列不唯一,故V4、V5谁为栈顶无所谓,这里V4为栈顶(其实入栈顺序与网的邻接表有关))
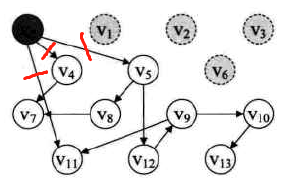
此时的输出序列: V3→V1→V2→V6→V0 -
由于V4在栈顶,故V4出栈,输出V4,并删除网所有以V4为出发点的弧。
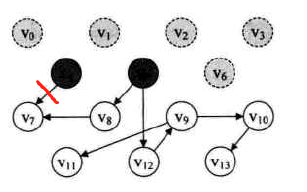
此时的输出序列: V3→V1→V2→V6→V0→V4
8.此时栈中只有V5了。输出V5,同时V5出栈,并删除网所有以V5为出发点的弧。(此时的 V8、V12的入度变为0,故 V8、V12进栈,设 V8在栈顶)
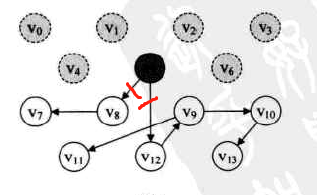
此时的输出序列: V3→V1→V2→V6→V0→V4→V5
-
由于V8在栈顶,故V8出栈,输出V8,并删除网所有以V8为出发点的弧。(此时V7的入度变为0,故V7入栈,并位于栈顶)
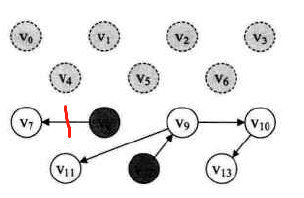
此时的输出序列: V3→V1→V2→V6→V0→V4→V5→V8 -
此时栈中只有V7了。输出V7,同时V7出栈,并删除网所有以V7为出发点的弧(没有弧可删)。
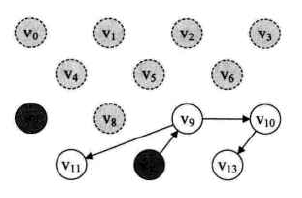
此时的输出序列: V3→V1→V2→V6→V0→V4→V5→V8→V7 -
此时栈中只有V12了。输出V12,同时V12出栈,并删除网所有以V12为出发点的弧。(此时的 V9的入度变为0,故 V9进栈)
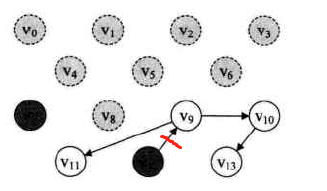
此时的输出序列: V3→V1→V2→V6→V0→V4→V5→V8→V7→V12
- 此时栈中只有V9了。输出V9,同时V9出栈,并删除网所有以V9为出发点的弧。(此时的 V10、 V11的入度变为0,故 V10、 V11进栈,V10为栈顶)
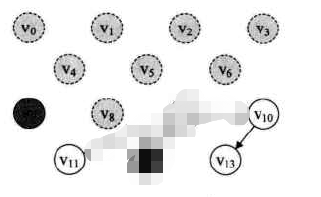
此时的输出序列: V3→V1→V2→V6→V0→V4→V5→V8→V7→V12→V9
13.此时的栈为{(栈底)V11、V10(栈顶)},故V10出栈,输出V10,删除V10为出发点的弧后,V13的入度变为0,故V13入栈。因此,最后一次输出V10→V13→V11。
因此,最终的输出序列: V3→V1→V2→V6→V0→V4→V5→V8→V7→V12→V9→V10→V13→V11








 本文详细介绍了图的拓扑排序,包括AOV网的定义、AOE网的定义、拓扑序列的定义以及拓扑排序的定义。通过具体的例子展示了如何使用邻接表对AOV网进行拓扑排序,逐步解释了每个步骤,并给出了一个完整的输出序列。
本文详细介绍了图的拓扑排序,包括AOV网的定义、AOE网的定义、拓扑序列的定义以及拓扑排序的定义。通过具体的例子展示了如何使用邻接表对AOV网进行拓扑排序,逐步解释了每个步骤,并给出了一个完整的输出序列。
















 6708
6708

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








