排序算法(尽量博采众长)
排序算法的对比
| 排序算法 | 最好情况 | 平均情况 | 最差情况 | 空间复杂度 | 稳定性 | 类别 |
|---|---|---|---|---|---|---|
| 快速排序 | n log n n\log n nlogn | n log n n\log n nlogn | n 2 n^2 n2 | log n \log n logn | 不稳定 | 比较/交换 |
| 冒泡排序 | n n n | n 2 n^2 n2 | n 2 n^2 n2 | 1 | 稳定 | 比较/交换 |
| 堆排序 | n log n n\log n nlogn | n log n n \log n nlogn | n log n n \log n nlogn | 1 | 不稳定 | 比较/选择 |
| 选择排序 | n n n | n 2 n^2 n2 | n 2 n^2 n2 | 1 | 不稳定 | 比较/选择 |
| 归并排序 | n log n n\log n nlogn | n log n n \log n nlogn | n log n n \log n nlogn | n n n | 稳定 | 比较/归并 |
| 插入排序 | n n n | n 2 n^2 n2 | n 2 n^2 n2 | 1 | 稳定 | 比较/插入 |
| 希尔排序 | n log n n \log n nlogn | n 4 / 3 n^{4/3} n4/3 | n 3 / 2 n^{3/2} n3/2 | 1 | 不稳定 | 比较/插入 |
| 计数排序 | n + m a x V − m i n V n+maxV-minV n+maxV−minV | m a x V − m i n V maxV-minV maxV−minV | 稳定 | 非比较类 | ||
| 桶排序 | n + k n+k n+k | n + k n+k n+k (k 桶个数) | 稳定 | 非比较类 | ||
| 基数排序 | n d nd nd | n + k n+k n+k (k进制) | 稳定 | 非比较类 |
排序算法详解
快速排序
原理
快速排序是一种基于分治思想的排序算法,它的基本思想是选择一个基准值,将待排序数组分成两部分,一部分比基准值小,另一部分比基准值大,然后对这两部分分别进行递归排序,最终将整个序列排序完成。
具体来说,快速排序的步骤如下:
- 选定一个基准值pivot,将待排序数组分成两部分:小于pivot的部分和大于等于pivot的部分。
- 对小于pivot的部分和大于等于pivot的部分分别递归调用快速排序。
- 合并两部分排序结果。
在实现快速排序时,一般采用双指针法来进行分区操作。具体来说,从左侧选择一个指针i,从右侧选择一个指针j。从右到左扫描(j),遇到比基准值小的元素就停下来,然后从左到右扫描,遇到比基准值大的元素就停下来。循环往复,直到i和j相遇,将基准值与相遇位置的元素交换。这样,基准值左边的元素就都小于基准值,右边的元素就都大于等于基准值。
快排需要注意,如果要升序排序那么需要先从右开始向左扫描。因为j停止的条件是当前元素小于pivot,i停止的条件是当前元素大于pivot。如果先从左开始扫描,那么i停止位置的元素大于pivot,那么这个时候交换它和pivot会导致大于pivot的元素交换到pivot的左边。

代码
def quick_sort(nums, low, high):
if low < high:
# divide and put the pivot in the correct position
pivot = partition(nums, low, high)
quick_sort(nums, low, pivot - 1) # conquer
quick_sort(nums, pivot + 1, high) # conquer
return nums
def partition(nums, low, high):
pivot = nums[low]
while low < high:
# from right to left
while low < high and nums[high] >= pivot:
high -= 1
# from left to right
while low < high and nums[low] <= pivot:
low += 1
nums[low], nums[high] = nums[high], nums[low]
# put the pivot in the correct position
nums[low], nums[0] = nums[0], nums[low]
return low
简洁一点的代码
def quick_sort_brief(nums):
if len(nums) <= 1: # Termination condition of recursion
return nums
else:
pivot = nums[0]
# left is smaller than pivot
left = [each for each in nums[1:] if each < pivot]
# right is not smaller than pivot
right = [each for each in nums[1:] if each >= pivot]
# recursion
return three_way_quick_sort(left) + [pivot] + three_way_quick_sort(right)
优化
快速排序对于时间复杂度的降低在于pivot可以把数组分割为子数组,如果数组处于基本有序状态那么pivot对数组的分割效果就会下降严重,时间复杂度最差会退化到 n 2 n^2 n2。
1. 那么对于快速排排序的一种优化就是改进pivot的选择方式。我们可以随机取三个值,然后取三个值中中间的那一个作为pivot。
2. 还可以改进分支的过程,分治的最后阶段,数组很短了,可以使用插入排序代替快排。
2. 三路快速排序可以有效地处理待排序数组中有大量重复元素的情况。具体思路是将待排序数组分成三部分:小于枢纽元、等于枢纽元和大于枢纽元。然后对小于和大于枢纽元的两部分进行递归排序,而对于等于枢纽元的部分则不需要再排序,可以直接跳过。这样可以减少重复元素的比较和移动次数,提高排序效率。
def three_way_quick_sort(nums):
if len(nums) <= 1: # Termination condition of recursion
return nums
else:
pivot = nums[0] # choose the first element as pivot
# left is smaller than pivot
left = [each for each in nums if each < pivot]
# right is bigger than pivot
right = [each for each in nums if each > pivot]
# mid is equal to pivot, it doesn't to be sorted.
mid = [each for each in nums if each == pivot]
# recusion
return three_way_quick_sort(left) + mid + three_way_quick_sort(right)
冒泡排序
原理
冒泡排序重复遍历整个数组,比较相邻的两个元素,如果它们的顺序不正确,就交换它们的位置。

代码
def bubble_sort(nums):
for i in range(len(nums) - 1):
for j in range(len(nums) - 1 - i):
# Big elements bubble towards the end
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
return nums
优化
- 设置flag,当某一轮不产生位置交换时,数组已经有序,此时可以结束排序
- 记录有序区间:每次排序时,记录最后一次交换的位置,该位置后面的元素已经有序,下一轮排序时无需再比较。
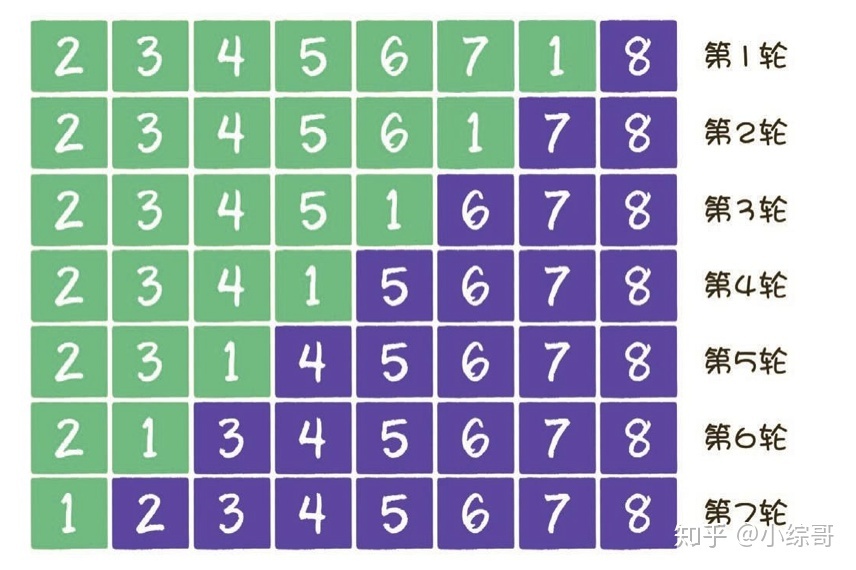
- 鸡尾酒排序:它的思想是在每一轮排序中同时从两端开始进行冒泡排序,即先从左往右进行一次冒泡排序,然后再从右往左进行一次冒泡排序。这样可以减少排序的时间,尤其是在序列大致有序的情况下。如下图所示,只有1是无序状态,但是却进行了7轮才完成排序。那么,可以考虑鸡尾酒排序的形式对其进行优化。
def cocktail_sort(nums):
left, right = 0, len(nums)-1
while left < right:
flag = False
# Forward
for i in range(left, right):
if nums[i] > nums[i+1]:
nums[i], nums[i+1] = nums[i+1], nums[i]
flag = True
right -= 1
# Reverse
for i in range(right, left, -1):
if nums[i] < nums[i-1]:
nums[i], nums[i-1] = nums[i-1], nums[i]
flag = True
left += 1
if not flag:
break
return nums
堆排序
原理
它的基本思想是将待排序的序列构造成一个堆,堆顶元素是序列中最大或最小的元素,将堆顶元素与序列末尾的元素交换,然后对序列前n-1个元素重新构造堆,依次类推直到排序完成。
堆是一种特殊的树形数据结构,满足堆的性质:对于一棵完全二叉树,每个节点的值都大于等于(或小于等于)它的子节点的值。我们把堆分为最大堆和最小堆两种。
堆排序的实现需要解决两个问题:如何构建初始堆和如何排序。
构建初始堆可以从最后一个非叶子节点开始,依次往上调整。排序时,先将堆顶元素与末尾元素交换,然后将堆的大小减1,重新调整堆,重复以上步骤直到堆的大小为1。排序完成后,序列就变成了有序的。
升序排序用大根堆,降序排序用小根堆。

代码
def heap_sort(nums):
n = len(nums)
# build min heap
for i in range(n // 2 - 1, -1, -1):
heapify(nums, n, i)
# Swap the minimum values to the end and take the minimum values in turn
# attention: the range of i is [n-1, 1], not [n-1, 0]
for i in range(len(nums) - 1, 0, -1):
nums[0], nums[i] = nums[i], nums[0]
heapify(nums, i, 0) # adjust the heap, the length of heap is i not n
print(nums)
def heapify(nums, n, i):
"""
Adjust the subtree rooted at i to be a min heap
"""
left = 2 * i + 1
right = 2 * i + 2
smallest = i
if left < n and nums[left] < nums[smallest]:
smallest = left
if right < n and nums[right] < nums[smallest]:
smallest = right
if smallest != i:
nums[i], nums[smallest] = nums[smallest], nums[i]
heapify(nums, n, smallest)
return nums
选择排序
原理
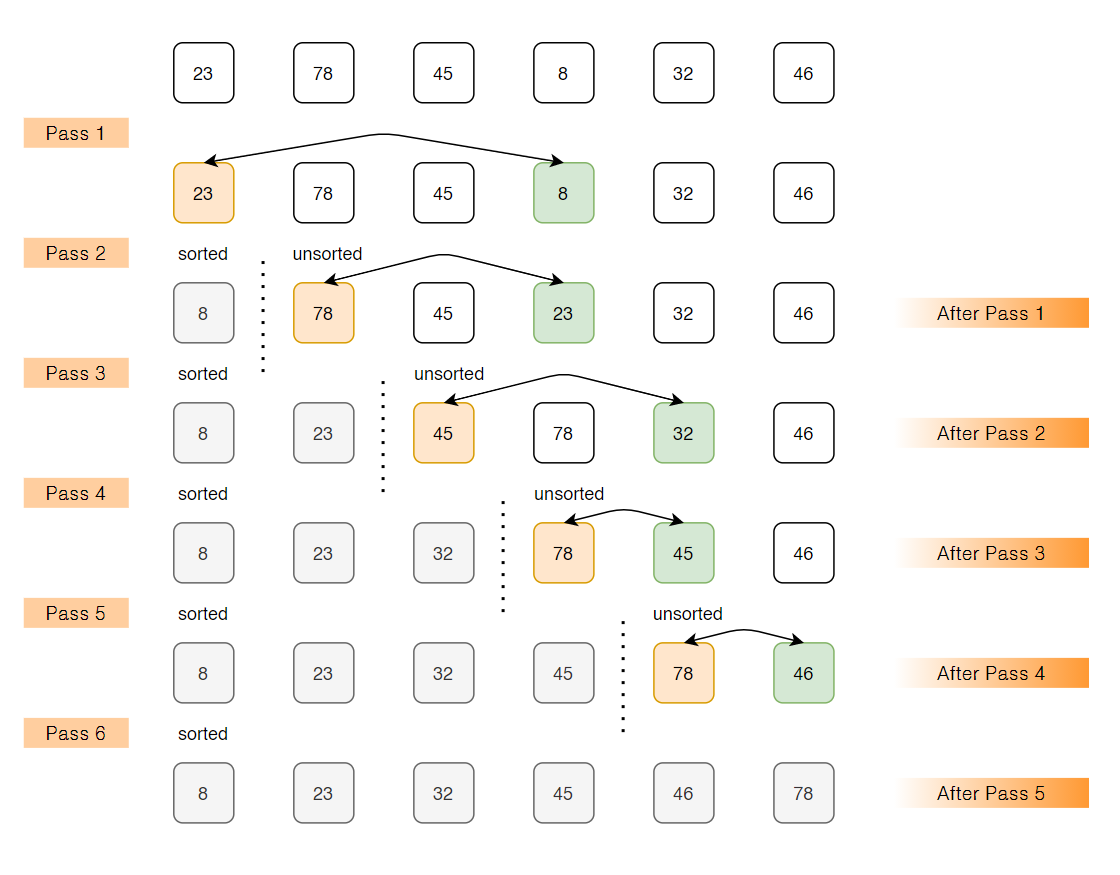
首先找到待排序数组中最小元素,并将其放到数组的最前面,然后再找到剩下的元素中最小的元素,放在已排序元素的后面,依次重复这个过程,直到整个数组都被排序。
具体实现过程如下:
- 遍历整个数组,找到最小的元素;
- 将最小元素与数组第一个元素交换位置;
- 对剩下的元素重复以上两个步骤,直到整个数组被排序。
在每一轮中,选择排序只需要进行一次交换,因此它在某些情况下可能比其他排序算法更加高效。但是,它的时间复杂度为 O(n^2),因此对于大规模的数据排序来说,选择排序并不是一个最优的选择。
代码
def select_sort(nums):
for i in range(0, len(nums) - 1):
smallest = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[smallest]:
smallest = j
nums[i], nums[smallest] = nums[smallest], nums[i]
print(nums)
归并排序
原理
归并排序的原理是将一个数组不断拆分成两个小数组,直到每个小数组只有一个元素为止,然后将这些小数组进行合并,合并时按照从小到大的顺序将元素逐个加入到一个新的数组中,最终得到的新数组就是排好序的。
具体实现时,归并排序可以采用递归的方法,即先将左半部分排序,再将右半部分排序,最后将左右两部分合并。合并时可以先复制两部分的元素到一个临时数组中,然后按照顺序比较两部分的元素,逐个加入到新数组中,直到其中一部分的元素全部加入完成,然后将剩下的另一部分的元素依次加入到新数组中。
归并排序递归的终止条件为数组长度为1,那么只有一个元素的数组自然为有序状态。

代码
def merge(left, right):
i, j = 0, 0
sorted_nums = []
while i < len(left) and j < len(right):
if left[i] <= right[j]:
sorted_nums.append(left[i])
i += 1
else:
sorted_nums.append(right[j])
j += 1
if i < len(left):
sorted_nums.extend(left[i:])
if j < len(right):
sorted_nums.extend(right[j:])
return sorted_nums
def merge_sort(nums):
# termination condition of recusion
if len(nums) <= 1:
return nums
mid = len(nums) // 2
# sort left and right
left = merge_sort(nums[:mid])
right = merge_sort(nums[mid:])
# merge two sorted arr
return merge(left, right)
优化
因为合并两个已排序的子数组时需要额外的空间存储,这就导致了空间复杂度为 O ( n ) O(n) O(n)。如果原地归并,也就是直接在原数组上进行合并,那么就需要使用额外的空间来暂存子数组的一部分,这样的空间复杂度也是 O ( n ) O(n) O(n)。
为了减小空间复杂度,可以考虑使用原地归并的方法,但是需要注意到在进行合并操作时,如果右半部分的第一个元素小于左半部分的最后一个元素,那么左半部分的所有元素都应该移动到右半部分,这就需要一个缓存数组暂存左半部分的元素,这个缓存数组的长度为 n / 2 n/2 n/2,因此空间复杂度为 O ( n / 2 ) O(n/2) O(n/2)。这样就将归并排序的空间复杂度降低到了 O ( n / 2 ) O(n/2) O(n/2),但时间复杂度仍然是 O ( n log n ) O(n\log n) O(nlogn)。这种实现方式称为“自然归并排序”。
另一种减小归并排序空间复杂度的方法是使用“循环赛制”,这种实现方式每次只需要申请一半大小的额外空间即可完成排序,但需要进行多次遍历和比较,时间复杂度会略有增加,不过在实际应用中仍然是比较高效的。
插入排序
原理
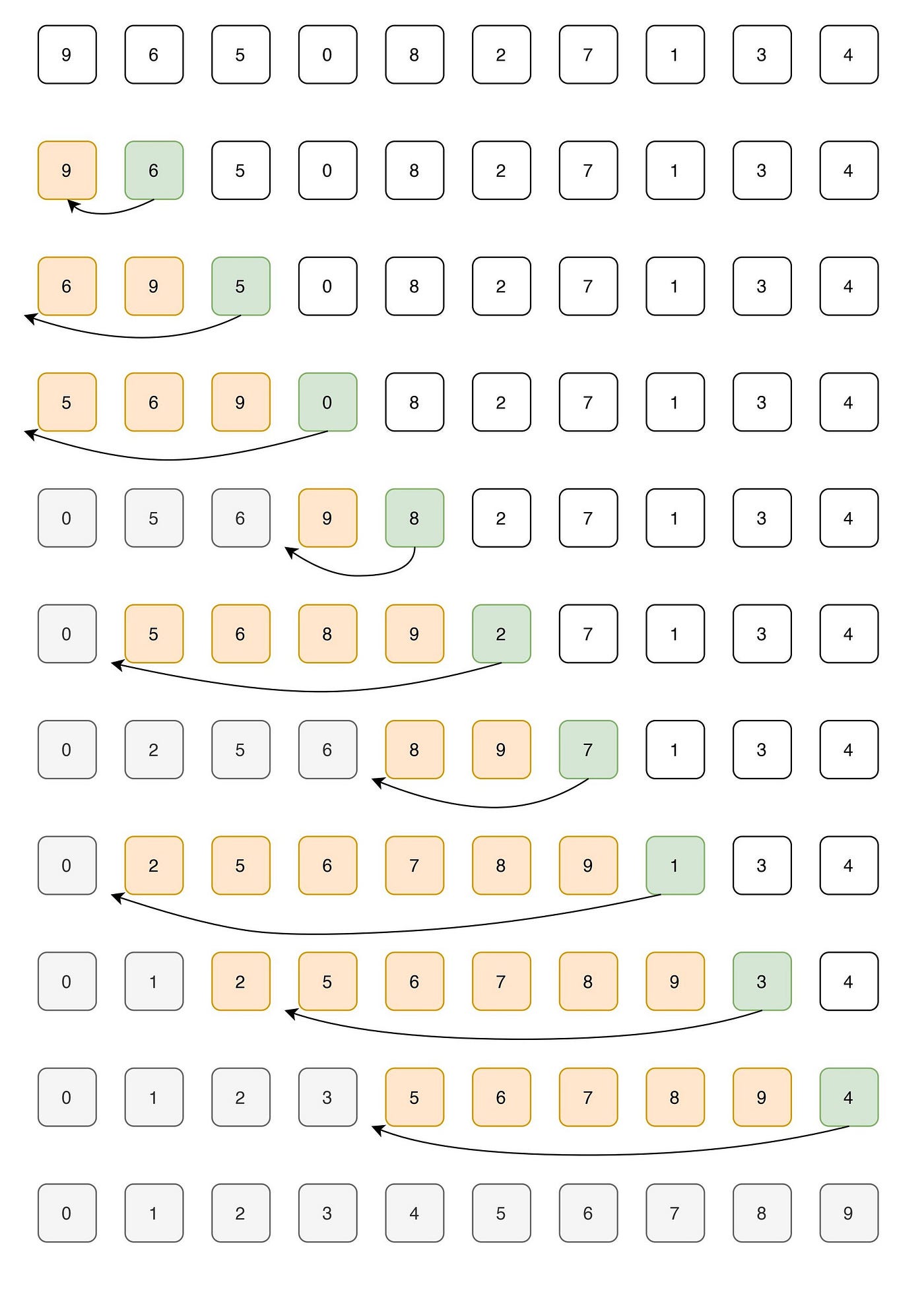
插入排序是一种简单直观的排序算法,其基本思想是将一个待排序的数组分为已排序和未排序两部分,然后每次从未排序部分选择一个元素插入到已排序部分的合适位置,最终使得整个数组有序。
具体实现方式如下:
- 将待排序数组分为已排序和未排序两部分,初始时已排序部分只包含一个元素,即数组的第一个元素;
- 遍历未排序部分的所有元素,依次将每个元素插入到已排序部分的合适位置。具体做法是将该元素与已排序部分的元素从后往前比较,找到第一个小于该元素的位置,然后将该元素插入到该位置后面;
- 重复步骤 2 直到未排序部分的所有元素都被插入到已排序部分为止。
插入排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( 1 ) O(1) O(1)。虽然插入排序的时间复杂度较高,但是由于其实现简单,常数较小,因此在小规模数据的排序中性能较优。
代码
def insert_sort(nums):
for i in range(1, len(nums)):
# The elements before i is an ordered sequence
j = i
while j > 0 and nums[j] < nums[j-1]:
nums[j], nums[j-1] = nums[j-1], nums[j]
j -= 1
print(nums)
优化
折半插入排序(Binary Insertion Sort):折半插入排序是对直接插入排序的一种优化,它在查找插入位置时采用了折半查找,可以提高查找的效率,从而减少了比较的次数。折半插入排序的时间复杂度为 O(n^2),空间复杂度为 O(1)。
def binary_insertion_sort(nums):
for i in range(1, len(nums)):
# The elements before i is an ordered sequence
temp = nums[i]
low, high = 0, i - 1
# binary search
while low <= high:
mid = (low + high) // 2
if temp < nums[mid]:
high = mid - 1
else:
low = mid + 1
# Move the elements after the insertion position to the right
for k in range(i - 1, high, -1):
nums[k + 1] = nums[k]
nums[high + 1] = temp
print(nums)
希尔排序(Shell Sort):希尔排序是对插入排序的一种优化,它采用了分组的思想,先将数组分成若干个小组进行插入排序,然后逐渐减小组的大小,最终进行一次全局的插入排序。希尔排序的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn) 到 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( 1 ) O(1) O(1)。希尔排序的优势在于能够在 O ( n log n ) O(n\log n) O(nlogn) 的时间内对大规模数据进行排序,而且相对于其他 O ( n log n ) O(n\log n) O(nlogn) 的排序算法,希尔排序的常数因子比较小,因此实际应用中表现较优。
希尔排序
原理
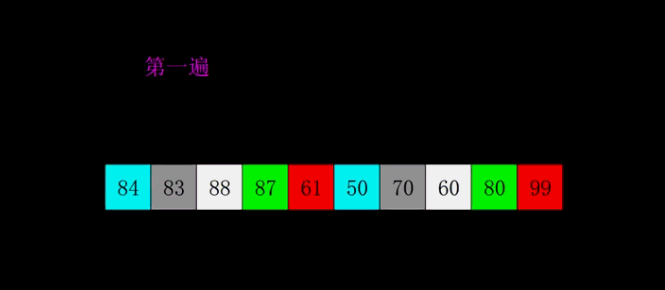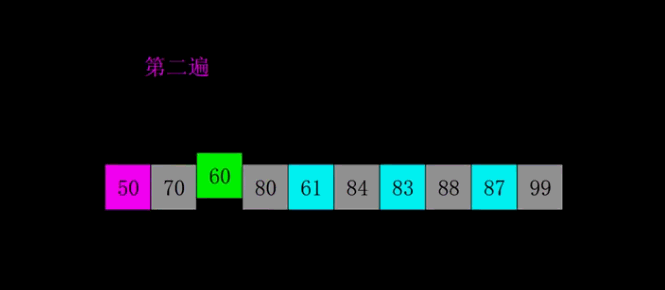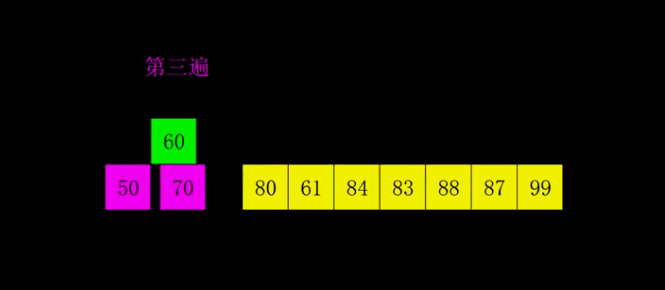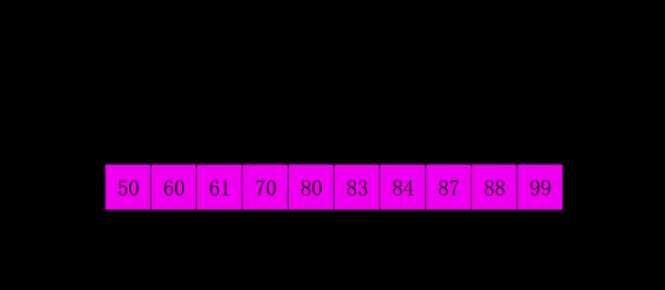
希尔排序,也称为缩小增量排序,是插入排序的一种改进版本。该算法的基本思想是将原始数组分成若干个子数组,对每个子数组进行插入排序,随后逐步减少子数组的数量并逐步增加每个子数组的元素数量,最终完成排序。
希尔排序的优化在于,它使用了增量序列来进行子数组划分,不同的增量序列会影响到排序的效率。常见的增量序列有希尔增量、Knuth增量等,它们可以提高排序的效率,使排序的时间复杂度达到O(nlogn)。
希尔排序的基本思路如下:
- 选择一个增量序列,如希尔增量h1 = n/2, h2 = h1/2, h3 = h2/2, … hn = 1
- 对每个增量 hi,将数组划分成若干个子数组,每个子数组包含相邻间隔为 hi 的元素,对每个子数组进行插入排序
- 逐渐减小增量 hi 的值,重复步骤 2,直至 hi = 1
代码
def shell_sort(nums):
n = len(nums)
# Start with a gap of n/2, and keep dividing by 2 until gap = 1
gap = n // 2
while gap > 0:
# Perform insertion sort on each subarray defined by the current gap
for i in range(gap, n):
temp = nums[i]
j = i
# Shift elements to the right until the correct position is found
while j >= gap and nums[j - gap] > temp:
nums[j] = nums[j - gap]
j -= gap
nums[j] = temp
gap //= 2
print(nums)
计数排序
原理
计数排序(Counting Sort)是一种非比较排序算法,它的基本思想是统计待排序序列中各元素出现的次数,再根据各元素出现的次数以及元素之间的大小关系,推导出每个元素在排序后所处的位置。
计数排序算法的步骤如下:
- 扫描整个待排序序列,统计每个元素出现的次数,即生成一个计数数组。计数数组的下标为待排序序列中的元素值,对应的元素值表示该元素出现的次数。
- 将计数数组进行顺序求和,即依次将当前元素与前面的元素累加,得到一个累加计数数组。此时,累加计数数组中的元素值表示的是待排序序列中小于或等于当前元素值的元素的个数。
- 从后往前扫描待排序序列,根据累加计数数组中的元素值确定当前元素在排序后的位置。具体地,假设当前待排序元素为 x,它在计数数组中的下标为 i,则 x 在排序后的位置为 sum[i] - 1,同时 sum[i] 需要减去 1 表示该位置已经被占用。
- 将排序后的元素复制到一个新的序列中,即可得到排好序的序列。
计数排序的时间复杂度为 O(n + k),其中 n 是待排序序列的长度,k 是元素取值范围。计数排序是一种稳定的排序算法,适用于元素取值范围较小的情况。但是,如果元素取值范围过大,将会消耗较多的空间,不适合使用计数排序。
代码
def count_sort(nums):
min_ = min(nums)
max_ = max(nums)
count = [0] * (max_ - min_ + 1)
for num in nums:
count[num-min_] += 1
# pre summary
for i in range(1, len(count)):
count[i] += count[i-1]
sorted_nums = [0] * len(nums)
# for i in range(len(nums)-1, -1, -1):
# sorted_nums[count[nums[i]-min_]-1] = nums[i]
# count[nums[i]-min_] -= 1
for num in reversed(nums):
sorted_nums[count[num-min_]-1] = num
count[num-min_] -= 1
print(sorted_nums)
桶排序
原理
桶排序是一种线性排序算法,适用于对一定范围内的整数排序。它的基本思想是将要排序的数据分配到有限数量的桶中,然后每个桶再单独进行排序,最后将每个桶中的数据按照次序依次取出,组成有序序列。具体步骤如下:
- 将待排序元素划分到不同的痛。先扫描一遍序列求出最大值 maxV 和最小值 minV ,设桶的个数为 k ,则把区间 [minV, maxV] 均匀划分成 k 个区间,每个区间就是一个桶。将序列中的元素分配到各自的桶。
- 对每个桶内的元素进行排序。可以选择任意一种排序算法。
- 将各个桶中的元素合并成一个大的有序序列。
假设数据是均匀分布的,则每个桶的元素平均个数为 n/k 。假设选择用快速排序对每个桶内的元素进行排序,那么每次排序的时间复杂度为 O ( n / k log ( n / k ) ) O(n/k \log(n/k)) O(n/klog(n/k)) 。总的时间复杂度为 O ( n ) + O ( k ) O ( n / k log ( n / k ) ) = O ( n + n log ( n / k ) ) = O ( n + n log n − n log k ) O(n)+O(k)O(n/k \log(n/k)) = O(n+n\log (n/k)) = O(n+n\log n-n \log k) O(n)+O(k)O(n/klog(n/k))=O(n+nlog(n/k))=O(n+nlogn−nlogk)。当 k 接近于 n 时,桶排序的时间复杂度就可以近似认为是 O ( n ) O(n) O(n) 的。即桶越多,时间效率就越高,而桶越多,空间就越大。
代码
def bucket_sort(nums, bucket_size=5):
max_ = max(nums)
min_ = min(nums)
bucket_count = (max_ - min_) // bucket_size + 1
# initialize the buckets
buckets = [[] for _ in range(bucket_count)]
# divide the data into buckets
for num in nums:
buckets[(num - min_) // bucket_size].append(num)
sorted_nums = []
for bucket in buckets:
# sort each bucket
bucket.sort()
# merge every bucket
sorted_nums.extend(bucket)
print(sorted_nums)
基数排序
原理
基数排序(Radix Sort)是一种非比较排序算法,它根据键值的每位数字来排序。它的时间复杂度为O(d(n+k)),其中d是数字位数,n是待排序数据个数,k是关键字的基数。
基数排序的基本思路是:将待排序的数字按照个位、十位、百位等位数上的数字分别进行排序,每次排序后根据排序结果重新排列待排序数组,重复上述过程直到所有位数上的数字都被排序完成。
基数排序可以采用LSD(Least Significant Digit)和MSD(Most Significant Digit)两种方式实现,其中LSD的实现较为简单,通常先对低位进行排序,再对高位进行排序。MSD则需要递归地对高位进行排序。
基数排序通常适用于位数较小的数列。
代码
def bucket_sort(nums):
max_len = len(str(nums))
for i in range(max_len):
buckets = [[] for _ in range(10)]
for num in nums:
buckets[num // (10 ** i) % 10].append(num)
nums = [num for bucket in buckets for num in bucket]
print(nums)
计数排序、基数排序和桶排序
- 基数排序和计数排序都可以看作是桶排序。
- 计数排序本质上是一种特殊的桶排序,当桶的个数取最大( maxV-minV+1 )的时候,就变成了计数排序。
- 基数排序也是一种桶排序。桶排序是按值区间划分桶,基数排序是按数位来划分;基数排序可以看做是多轮桶排序,每个数位上都进行一轮桶排序。
引用
自己的学习笔记,引用了如下图片,感谢原作者,侵删。























 511
511

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








