深度学习 激活函数理解

一、首先需要准备一个反向传播的例子。

举例：假设一个有两个隐藏层，每个隐藏层有一个神经元且接着一个sigmoid激活函数的神经网络例子，输入为x0,输出为pre，真实值为rel,经过第一个线性层为x11,第一个激活函数为x12;第二个线性层为x21,第二个激活函数为x22

1.

首先需要知道输出：pre = sig(w2*sig(w1*x0+b1)+b2) = sig(w2*x12+b2)  ,  x12 = sig(w1*x0+b1)

权重更新公式：w-a*df/dw （a为梯度的学习率）   ,激活函数sig(x)=1/（1+exp(-x)）对x求导为 sig(x)*(1-sig(x))

损失值为L2：loss = (pre-rel)**2

2.

1.计算w2权重更新变化值：df/dw2 = (dloss/dpre) * (dpre/dw2) = 2*(pre-rel) * sig(w2*x12+b2) * (1-sig(w2*x12+b2)) * x12

2.计算w1权重更新变化值：df/dw1 = (dloss/dpre) * (dpre/dx12) * (dx12/dw1) = (dpre/dx12)  *  sig(w1*x0+b1) * (1-sig(w1*x0+b1))  *  x0  = 2*(pre-rel)  * [ sig(w2*x12+b2) * (1-sig(w2*x12+b2)) ] * w2  * [sig(w1*x0+b1) * (1-sig(w1*x0+b1)) ] *  x0 

为简化方程 ： df/dw1 =  (pre-rel) * A * w2 * B *x0 , df/dw1 = (pre-rel) * A * x12  

其中  A，B 为sigmoid激活函数的偏导，恒大于 0 且 小于0.25

二、以Sigmoid和Relu两个激活函数举例

1.Sigmoid 

  

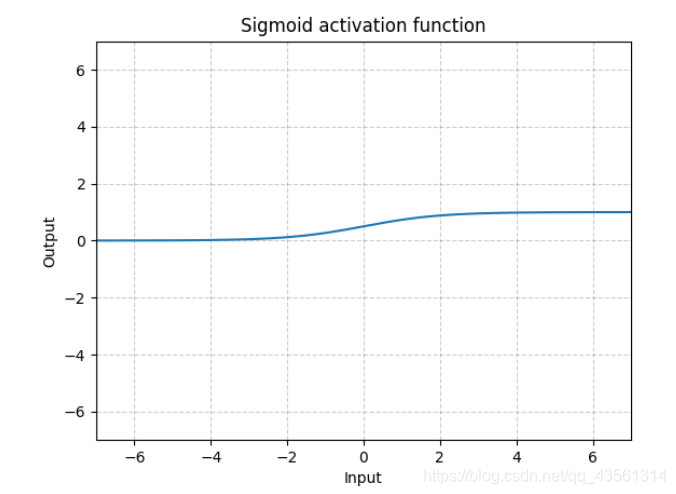
显而易见三个特征：

1.该激活函数将输入该激活函数的值压缩在了0-1之间

2.非0均值

3.数字越大或者越小，其梯度几乎无变化。

因此引发两个问题：

1. 当输入值非常大或者非常小时，神经元权重变化趋近于0，相当于“死去”，权重无更新。如第一部分的公式：df/dw2 = 2*(pre-rel) * sig(w2*x12+b2) * (1-sig(w2*x12+b2)) * x12 ，当x12极大或极小时，sig(w2*x12+b2) * (1-sig(w2*x12+b2))趋近于0，因此df/dw2无变化。df/dw1同理。

2.非0均值问题。激活函数的输出值恒大于 0，将会导致激活函数下一层的线性层权重w朝一个方向变化,既 不会朝相反方向变化（只会增大或只会减小）。如第一部分的w2的变化值：dpre/dw2 = sig(w2*x12+b2) * (1-sig(w2*x12+b2)) * x12 ，无论x11是大于还是小于0，x12恒大于0，导致dpre/dw2的都为正或负。(可以控制该层学习率减小这种问题。)

2.Relu

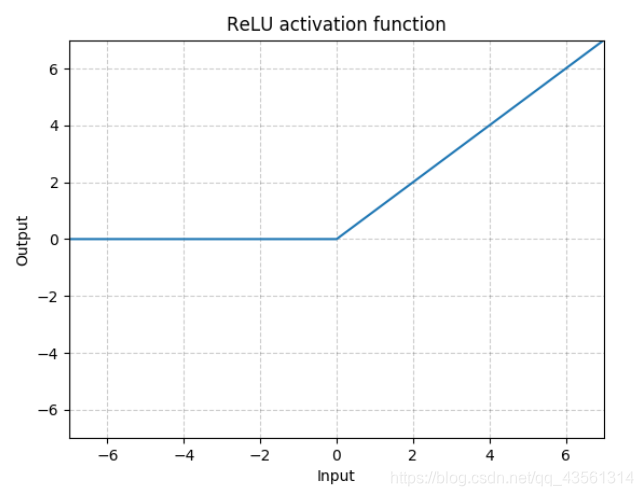
显而易见，x<0时，值和斜率都等于0；x>0时，斜率等于1.

因此优点很明显，收敛的速度快，小于0的部分直接忽略。大于0的部分直接乘以1（relu求导为1）

缺点：该神经元很容易“死去” 当x>0时，以第一部分举例，把sigmoid换成Relu: 当下输入值x0很大时 df/dw1 =  (pre-rel) * 1 * w2 * 1 *x0，df/dw1的改变值就很大，后面就不容易改正。

一般不能放置于最后一层，不然这么多零。

 

三、引出的其他问题。

1.为什么激活函数斜率为正？保持损失值函数为凸函数，然后优化器使变化朝斜率变化小的方向走。并且越接近最小值，其斜率越小，所以需要更小的学习率来逼近最优点。

2.为什么部分激活函数x<0时，斜率为0或趋近于0; x>0时斜率又比较大。如：ReLU、Softplus、CELU。有什么作用？

首先，梯度的变化值大小的影响因素可从第一部分（df/dw1 =  (pre-rel) * A * w2 * B *x0 ，w-a*df/dw ）看出，有五方面：1.a（梯度的学习率，可在优化器中设置）;2.后面隐藏层的权重; 3.激活函数的斜率 ;4. 当前层输入的x; 5.pre。然而我们可以直接控制的有两个，分别是第一和第三点。

其次，我们需知道梯度变化情况容易造成的问题。当梯度变化过大时：刚开始学习速度快，但容易造成损失值爆炸，易震荡的缺点（可以通过loss的变化了解及控制）。梯度变化过小时：拟合速度慢，容易过拟合，且局部最优值。

下面就是我对这问题的思考：由于激活函数直接影响了梯度变化的大小，当x<0时，斜率为0或趋近于0时，该权重近乎无变化；而x>0时，权重变化相对较大。即在一定程度上加快了训练的速度且使得震荡小。又使得x<0的部分，权重几乎不更新，避免了局部最优值，有点点类似dropout。

达到更好的效果也可以尝试控制每一层的学习率来更好的控制梯度变化大小。并且总体训练过程，可以使得刚开始学习率大，一段时间或条件后，逐渐减小。

 

Reference

https://blog.youkuaiyun.com/cyh_24/article/details/50593400