【8. 栈、队列和数组】

原创已于 2025-02-17 11:34:12 修改

· 208 阅读

0 ·

版权

文章标签：

#数据结构

于 2024-11-19 17:28:52 首次发布

数据结构专栏收录该内容

20 篇文章

订阅专栏

栈、队列和数组笔记记录

1. 栈
2. 队列
3. 栈和队列的应用
4. 数组和特殊矩阵

1. 栈

1.1 栈的基本概念

栈的定义：栈(Stack)是只允许在一端进行插入或删除操作的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。

栈顶(Top)。线性表允许进行插入删除的那一端。
栈底(Bottom)。固定的，不允许进行插入和删除的另一端。
空栈。不含任何元素的空表。

特性：后进先出(Last In First Out,LIFO)。每接触一种新的数据结构，都应从其逻辑结构、存储结构和运算三个方面着手。
栈栈的基本操作：

InitStack(kS):初始化一个空栈s。
StackEmpty(S):判断一个栈是否为空，若栈s为空则返回 true,否则返回 false。
Push(&S,x):进栈，若栈 s未满，则将x加入使之成为新栈顶。
Pop(&S,&x):出栈，若栈s非空，则弹出栈顶元素，并用x返回。
GetTop(S,&x):读栈顶元素，但不出栈，若栈s非空，则用x返回栈顶元素。
DestroyStack(&S):销毁栈，并释放栈s占用的存储空间(“&”表示引用调用)。

栈的数学性质：卡特兰数公式。

1.2 栈的顺序存储结构

栈是一种操作受限的线性表，类似于线性表，它也有对应的两种存储方式。

顺序栈的实现：
采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针(top)指示当前栈顶元素的位置。
栈的定义
#define MAXSIZE 5
typedef struct{
int data[MAXSIZE];
int top;
}SqStack;

栈顶指针：S.top,初始时S.top=-1;
栈顶元素：S.data[S.top];
进栈操作：栈不满时，栈顶指针先加1,再送值到栈顶。
出栈操作：栈非空时，先取栈顶元素，再将栈顶指针减1。
另一种常见的方式是：初始设置栈顶指针 S.top=0;进栈时先将值送到栈顶，栈顶指针再加1:出栈时，栈顶指针先减 1,再取栈顶元素；栈空条件是 S.top==0;栈满条件是S.top= =MAXSIZE -1。

总结：

实际就是一个静态链表,s.top==-1说明现在是个空栈，如果栈满那么 S.top==MAXSIZE-1，相当于下标从0开始，到4结束。

#define MaxSzie 50
typedef struct {
    int data[MaxSize];
    int top;
}SqStack;

1.2.1 顺序栈的基本操作

#include "iostream"

using namespace std;
#define MAXSIZE 5
typedef struct {
    int data[MAXSIZE];
    int top;
} Stack;

//初始化栈
void initStack(Stack &S) {
    //初始化栈顶指针
    S.top = -1;
}

//判断栈是否为空
bool isEmpty(Stack S) {
    return S.top == -1;
}

//判断栈是否已经满了
bool isFull(Stack S) {
    return S.top == MAXSIZE - 1;
}

//进栈
bool push(Stack &S, int x) {
    //栈如果满了 直接返回false
    if (isFull(S)) {
        return false;
    } else {
        //先将栈顶指针加一，再赋值
        S.data[++S.top] = x;
        return true;
    }
}

//出栈
bool pop(Stack &S, int &x) {
    //栈如果为空 直接返回false
    if (isEmpty(S)) {
        return false;
    } else {
        //先赋值再将栈顶指针减一
        x = S.data[S.top--];
        return true;
    }
}

//遍历栈
void traverse(Stack S) {
    for (int i = 0; i <= S.top; i++) {
        cout << S.data[i] << " ";
    }
    cout << endl;
}

int main() {
    Stack S;
    initStack(S);
    push(S, 1);
    push(S, 2);
    push(S, 3);
    push(S, 4);
    push(S, 5);
    traverse(S);
}

1.2.2 共享栈

两个栈的栈顶指针都指向栈顶元素，top0=-1时0号栈为空，top1=MaxSize时1号栈为空；
仅当两个栈顶指针相邻(top1-top0=1)时，判断为栈满。当0号栈进栈时 top0 先加1再赋值，1号栈进栈时 top1先减1再赋值；出栈时则刚好相反。
上溢是指存储器满，还往里写；下溢是指存储器空，还往外读。**为了解决上溢，可给栈分配很大的存储空间，但这样又会造成存储空间的浪费。**共享栈的提出就是为了在解决上溢的基础上节省存储空间，将两个栈放在同一段更大的存储空间内，这样，当一个栈的元素增加时，可使用另一个栈的空闲空间，从而降低发生上溢的可能性。
● 共享栈为了解决上溢问题。

1.3 栈的链式存储结构

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头结点，Lhead 指向栈顶元素。
typedef struct Linknode(
ElemType data; //数据域
struct Linknode *next; //指针域
)LiStack; //栈类型定义
采用链式存储，便于结点的插入与删除。链栈的操作与链表类似，入栈和出栈的操作都在链
表的表头进行。

2. 队列

2.1 队列的基本概念

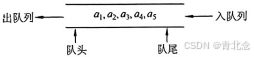
队列(Queue)简称队，也是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。向队列中插入元素称为入队或进队；删除元素称为出队或离队。这和我们日常生活中的排队是一致的，最早排队的也是最早离队的，其操作的特性是先进先出(First InFirst Out,FIFO).【队头出队，队尾入队】

栈和队列是操作受限的线性表，因此不是任何对线性表的操作都可以作为栈和队列的操作。比如，不可以随便读取栈或队列中间的某个数据。
队列的基本操作

InitQueue(&Q):初始化队列，构造一个空队列Q。
QueueEmpty(Q):判队列空，若队列Q为空返回 true,否则返回 false。
EnQueue(&Q,x):入队，若队列Q未满，将x加入，使之成为新的队尾。
DeQueue(&Q,&x):出队，若队列Q非空，删除队头元素，并用x返回。
GetHead(Q,&x):读队头元素，若队列Q非空，则将队头元素赋值给x。

2.2 队列顺序存储结构

2.2.1 队列的顺序存储

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素，并附设两个指针：队头指针front指向队头元素，队尾指针rear指向队尾元素的下一个位置(不同教材对front和rear的定义可能不同，例如，可以让rear指向队尾元素、front 指向队头元素。对）
初始时：Q.front=Q.rear=0。进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。出队操作：队不空时，先取队头元素值，再将队头指针加1。
为队列的初始状态，有Q.front= =Q.rear= =0成立，该条件可以作为队列判空的条件。但能否用Q.rear==MaxSize作为队列满的条件呢?显然不能，队列中仅有一个元素，但仍满足该条件。这时入队出现“上溢出”,但这种溢出并不是真正的溢出，在data数组中依然存在可以存放元素的空位置，所以是一种“假溢出”。

2.2.1 循环队列(解决顺序存储的【假溢出】)

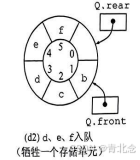
由于顺序队列“假溢出”的问题，这里引出循环队列的概念。将顺序队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环，称为循环队列。当队首指针Q.front=MaxSize-1后，再前进一个位置就自动到0,这可以利用除法取余运算(%实现。)

初始时：Q.front=Q.rear=0。
队首指针进1:Q.front=(Q.front+1)%MaxSize。
队尾指针进1:Q.rear=(Q.rear+1)%MaxSize。
队列长度：(Q.rear+MaxSize-Q.front)%MaxSize。
队空的条件是Q.front==Q.rear。

队满的判断有三种情况

1)牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是一种较为普遍的做法，约定以“队头指针在队尾指针的下一位置作为队满的标志”.队满条件：(Q.rear+1)%MaxSize= =Q.front。队空条件：Q.front==Q.rear。队列中元素的个数：(Q.rear-Q.front+MaxSize)%MaxSize。

2)类型中增设size数据成员，表示元素个数。删除成功 size减1,插入成功 size加1。队空时Q.size= =0;队满时Q.size= =MaxSize,两种情况都有Q.front==Q.rear。
3)类型中增设 tag 数据成员，以区分是队满还是队空。删除成功置tag=0,若导致Q.front==Q.rear,则为队空；插入成功置 tag=1,若导致 Q.front==Q.rear,则为队满。

2.2.3 循环队列的操作

#include "istream"
#define MAXSIZE 50
typedef struct {
    int data[MAXSIZE];
    int front,rear;
}Queue;
//队列初始化
void initQueue(Queue &Q){
    Q.front=Q.rear=0;
}
//队列是否为空
bool isEmpty(Queue Q){
    return Q.front==Q.rear;
}
//判断队列是否已满
bool isFull(Queue Q){
    return (Q.rear+1)%MAXSIZE==Q.front;
}
//入队
bool enQueue(Queue &Q,int x){
    if (isFull(Q)){
        return false;
    }
    Q.data[Q.rear]=x;
    //先放元素 后移动指针 front和rear刚开始在0位置，rear移动即可
    Q.rear=(Q.rear+1)%MAXSIZE;
    return true;
}
//出队
bool deQueue(Queue &Q,int &x){
    if (isEmpty(Q)){
        return false;
    }
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%MAXSIZE;
    return true;
}
int main() {

}

2.3 队列链式存储结构

2.3.1 队列的链式存储

队列的链式表示称为链队列，它实际上是一个同时有队头指针和队尾指针的单链表，如图3.8
所示。头指针指向队头结点，尾指针指向队尾结点，即单链表的最后一个结点。

链式队列声明

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode;
typedef struct{
    LNode *front,*rear;
}LinkQueue;

1 . 不带头结点时，当Q.front= =NULL且Q.rear= =NULL时，链式队列为空。
2. 入队时，建立一个新结点，将新结点插入到链表的尾部，并让Q.rear 指向这个新插入的结
点(若原队列为空队，则令Q.front也指向该结点)。出队时，首先判断队是否为空，若不空，则取出队头元素，将其从链表中摘除，并让 Q.front 指向下一个结点(若该结点为最后一个结
点，则置Q.front和Q.rear都为NULL)。不难看出，不带头结点的链式队列在操作上往往比较麻烦，因此通常将链式队列设计成一个带头结点的单链表，这样插入和删除操作就统一了。

用单链表表示的链式队列特别适合于数据元素变动比较大的情形，而且不存在队列满且产生溢出的问题。另外，假如程序中要使用多个队列，与多个栈的情形一样，最好使用链式队列，这样就不会出现存储分配不合理和“溢出”的问题。

2.3.2 链式队列的基本操作

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode;
typedef struct{
    LNode *front,*rear;
}LinkQueue;
void initQueue(LinkQueue &Q){
    Q.front=Q.rear=(LNode *)malloc(sizeof(LNode));
    Q.front->next=NULL;
}
bool isEmpty(LinkQueue Q){
    return Q.front==Q.rear;
}
bool enQueue(LinkQueue &Q,int x){
    LNode *s=(LNode *)malloc(sizeof(LNode));
    s->data=x;
    s->next=NULL;
    Q.rear->next=s;
    Q.rear=s;
    return true;
}
bool deQueue(LinkQueue &Q,int &x){
    if (isEmpty(Q)){
        return false;
    }
    LNode *p=Q.front->next;
    x=p->data;
    Q.front->next=p->next;
    if (Q.rear==p){
        Q.rear=Q.front;
    }
    free(p);
    return true;
}

2.4 双端队列

双端队列是指允许两端都可以进行插入和删除操作的线性表，如图3.10所示。双端队列两端
的地位是平等的，为了方便理解，将左端也视为前端，右端也视为后端。

在双端队列进队时，前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时，无论是前端还是后端出队，先出的元素排列在后出的元素的前面。
输出受限的双端队列许在一端进行插入和删除，但在另一端只允许插入的双端队列称为输出受限的双端队列。

输入受限的双端队列：允许在一端进行插入和删除，但在另一端只允许删除的双端队列称为输入受限的双端队列，如图3.12所示。若限定双端队列从某个端点插入的元素只能从该端点删除，则该双端队列就蜕变为两个栈底相邻接的栈。

例设有一个双端队列，输入序列为1,2,3,4,试分别求出以下条件的输出序列。
(1)能由输入受限的双端队列得到，但不能由输出受限的双端队列得到的输出序列。
(2)能由输出受限的双端队列得到，但不能由输入受限的双端队列得到的输出序列。
(3)既不能由输入受限的双端队列得到，又不能由输出受限的双端队列得到的输出序列。
其中不能通过输入受限的双端队列得到的是：4,2,3,1和4,2,1,3。
其中不能通过输出受限的双端队列得到的是：4,1,3,2和4,2,3,1。

1)能由输入受限的双端队列得到，但不能由输出受限的双端队列得到的是4,1,3,2。
2)能由输出受限的双端队列得到，但不能由输入受限的双端队列得到的是4,2,1,3。
3)既不能由输入受限的双端队列得到，又不能由输出受限的双端队列得到的是4,2,3,1。

3. 栈和队列的应用

3.1 栈在括号匹配中的应用

假设表达式中允许包含两种括号：圆括号和方括号，其嵌套的顺序任意即()或[([][])]等均为正确的格式，[(])或([())或(()]均为不正确的格式。
算法的思想如下：

1)初始设置一个空栈，顺序读入括号。
2)若是左括号，则作为一个新的更急迫的期待压入栈中，自然使原有的栈中所有未消解的期待的急迫性降了一级。
3)若是右括号，则或使置于栈顶的最急迫期待得以消解，或是不合法的情况(括号序列不匹配，退出程序)。算法结束时，栈为空，否则括号序列不匹配。

3.2 栈在表达式求值中的应用

括号匹配

#include <iostream>
#include <cstring>

using namespace std;
#define MaxSize 100001
typedef struct {
    char data[MaxSize]; //静态数组存放栈中元素
    int top;           // 栈顶元素
} SqStack;

void InitSqStack(SqStack &S) {
    S.top = -1;
}
bool StackEmpty(SqStack S) {
    return S.top == -1;
}
bool Push(SqStack &S, char x) {
    if (S.top == MaxSize - 1) {
        return false;
    }
    S.data[++S.top] = x;
    return true;
}
bool Pop(SqStack &S, char &x) {
    if (StackEmpty(S)) {
        return false;
    }
    x = S.data[S.top--];
    return true;
}
bool BracketCheck(char str[]) {
    SqStack S;
    InitSqStack(S);
    for (int i = 0; i < strlen(str); i++) {
        if (str[i] == '<' || str[i] == '(' || str[i] == '{' || str[i] == '[') {
            Push(S, str[i]);
        } else {
            char x;
            Pop(S, x);
            if (str[i] == '>' && x != '<')
                return false;
            if (str[i] == ')' && x != '(')
                return false;
            if (str[i] == '}' && x != '{')
                return false;
            if (str[i] == ']' && x != '[')
                return false;
        }
    }
    return StackEmpty(S);
}
int main() {
    char str[MaxSize];
    fgets(str, MaxSize, stdin);
    int len = strlen(str);
    if (len > 0 && str[len - 1] == '\n') {
        str[len - 1] = '\0';
    }
    if (BracketCheck(str)) {
        cout <<"yes"<<endl;
    }else{
        cout <<"no"<<endl;
    }
}

3.2.1 算术表达式

中缀表达式(如3+4)是人们常用的算术表达式，操作符以中缀形式处于操作数的中间。与前缀表达式(如+34)或后缀表达式(如34+)相比，中缀表达式不容易被计算机解析，但仍被许多程序语言使用，因为它更符合人们的思维习惯。与前缀表达式或后缀表达式不同的是，中缀表达式中的括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来，用于指示运算的次序。后缀表达式的运算符在操作数后面，后缀表达式中考虑了运算符的优先级，没有括号，只有操作数和运算符。中缀表达式A+B*(C-D)-E/F对应的后缀表达式为ABCD-*+EF/-,将后缀表达式与原表达式对应的表达式树(图3.15)的后序遍历序列进行比较，可发现它们有异曲同工之妙。

3.2.2 中缀表达式转后缀表达式

中缀A+B*(C-D)-E/F转后缀
1)加括号：((A+③(B*②(C-①D)))-⑤(E/④F))。
2)运算符后移：((A(B(CD)-①)②)+③(EF)/④)-⑤·
3)去除括号后，得到后缀表达式：ABCD-①②+③EF/④-⑤°

3.2.3 后缀表达式求值

3.3 栈在递归中的应用

3.4 队列在层次遍历中的应用

3.5 队列在计算机系统中的应用

第一个方面是解决主机与外部设备之间速度不匹配的问题.
第二个方面是解决由多用户引起的资源竞争问题。

对于第一个方面，仅以主机和打印机之间速度不匹配的问题为例做简要说明。主机输出数据
给打印机打印，输出数据的速度比打印数据的速度要快得多，因为速度不匹配，若直接把输出的
数据送给打印机打印，则显然是不行的。解**决的方法是设置一个打印数据缓冲区，主机把要打印
输出的数据依次写入这个缓冲区，写满后就暂停输出，转去做其他的事情。**打印机就从缓冲区中
按照先进先出的原则依次取出数据并打印，打印完后再向主机发出请求。主机接到请求后再向缓
冲区写入打印数据。这样做既保证了打印数据的正确，又使主机提高了效率。由此可见，打印数
据缓冲区中所存储的数据就是一个队列。
对于第二个方面，CPU(即中央处理器，它包括运算器和控制器)资源的竞争就是一个典型
的例子。在一个带有多终端的计算机系统上，有多个用户需要CPU各自运行自己的程序，它们分
别通过各自的终端向操作系统提出占用CPU 的请求。**操作系统通常按照每个请求在时间上的先后
顺序，把它们排成一个队列，每次把CPU分配给队首请求的用户使用。**当相应的程序运行结束或
用完规定的时间间隔后，令其出队，再把CPU 分配给新的队首请求的用户使用。这样既能满足每
个用户的请求，又使CPU能够正常运行。

4. 数组和特殊矩阵

矩阵在计算机图形学、工程计算中占有举足轻重的地位。在数据结构中考虑的是如何用最小的内存空间来存储同样的一组数据。所以，我们不研究矩阵及其运算等，而把精力放在如何将矩阵更有效地存储在内存中，并能方便地提取矩阵中的元素。

4.1 数组的定义

数组是由n(n≥1)个相同类型的数据元素构成的有限序列，每个数据元素称为一个数组元素，每个元素在n个线性关系中的序号称为该元素的下标，下标的取值范围称为数组的维界。数组与线性表的关系：数组是线性表的推广。一维数组可视为一个线性表；二维数组可视为其元素是定长数组的线性表，以此类推。数组一旦被定义，其维数和维界就不再改变。因此，除结构的初始化和销毁外，数组只会有存取元素和修改元素的操作。

4.2 数组的存储结构

大多数计算机语言都提供了数组数据类型，逻辑意义上的数组可采用计算机语言中的数组数据类型进行存储，一个数组的所有元素在内存中占用一段连续的存储空间。

多维数组：
对于多维数组，有两种映射方法：按行优先和按列优先。以二维数组为例，按行优先存储的基本思想是：先行后列，先存储行号较小的元素，行号相等先存储列号较小的元素。设二维数组的行下标与列下标的范围分别为[0,h1]与[0,h2],则存储结构关系式为：

3. 按照行存储公式为 LOC(ai,j)=LOC(a00)+[i*[列最大下标范围+1]+j]L 【a00+i列最大+j】L
4. 按照列存储公式为 LOC(ai,j)=LOC(a00)+[j[行最大下标范围+1]+i]L 【a00+j行最大+i】*L

4.3 特殊矩阵的压缩存储

压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配空同。
特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有对称矩阵、上(下)三角矩阵、对角矩阵等。
特殊矩阵的压缩存储方法：找出特殊矩阵中值相同的矩阵元素的分布规律，把那些呈现规律性分布的、值相同的多个矩阵元素压缩存储到一个存储空间中。