中国剩余定理

中国剩余定理

前言

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

公式

上面一段话可以理解成如下方程组：
整数m1,m2, … ,mn两两互质，则对任意的整数：a1,a2, … ,an，方程组有解

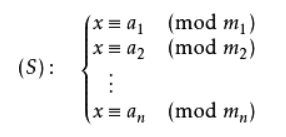
1. 令M=m1 * m2 * m3 * … * mn，M为最小公倍数，并设Mi = M/mi，为除了mi外n-1个数的乘积。(1 <= i <= n)
2. 设 ti=Mi^-1 为Mi的数论倒数,(ti 为 Mi 模 mi 意义下的逆元)，
   即ti * Mi=1(mod mi)，ti 可以由扩展gcd求得,将式子化成如下形式用扩展gcd(扩展gcd传送门)：
   (ti * Mi)%mi=1
   => ti * Mi - mi * (ti * Mi) / mi=1
   令a=ti，b=-(ti * Mi) / mi，x=Mi，y=(ti * Mi) / mi
   则原式为a * x+b * y=1，于是直接上exgcd
3. 则S的通解为：
   x=a1 * t1 * M1+a2 * t2 * Mi+ … +an * tn * Mi+kM =kM+${\sum }_{i=1}^n$ai * ti * Mi(k为整数)
   在模M的情况下
   x=(${\sum }_{i=1}^n$ai * ti * Mi)%M

证明

证明有点烦，于是偷懒百度一张图
由于上图已经很详细了，下面只给出简单证明：
ti * Mi≡1(mod mi)
两边同时乘ai
ai * ti * Mi≡ai * ≡ai (mod mi)
因为$\frac{M}{mi}$为除了mi以外的所有m的倍数
所以$\forall j̸=i$，ai​$\frac{M}{mi}$​ti​ ≡ 0(mod mj​)
所以
x=ai * ti * Mi+${\sum }_{j̸=i}^{}$aj * tj *Mj≡ai + 0≡ai(mod mi)