帮你搞懂Java二叉树，超详细解析，所有基础操作及五种遍历（深度，广度），求大小，求深度。(上)

前言

转载需经作者同意

熬了两天终于把二叉树所有基本操作全看明白了。加了自己想法，送给正在被二叉树折磨的你。。。
我将会从二叉树的定义出发，介绍什么是二叉树，有哪些相关内容，并穿插讲解其代码实现。
鉴于内容较多，将分为两篇文章进行讲解以便读者有时间去消化。（让我自己偷懒歇会儿😑😑😑）

正文

注：
1.以下代码使用了Java泛型，不懂的小伙伴可以评论区问。有必要的话我可以出一期专门讲讲泛型
2.思路讲解时，部分相关函数将不会展示完整代码。整体代码我会放到最后并注以必要的注释供大家参考

二叉树的概念

二叉树是每个结点最多有两个子树的树结构，树中存有数据以及子树。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

二叉树性质

在非空二叉树中，第i层的结点总数不超过, 2^(i-1),i>=1。
深度为h的二叉树最多有个结点(2^k)-1(k>=1)，最少有k个结点。

完全二叉树概念

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

完全二叉树性质

①n= n0+n1+n2 （其中n为完全二叉树的结点总数）；又因为一个度为2的结点会有2个子结点，一个度为1的结点会有1个子结点，除根结点外其他结点都有父结点，
②n= 1+n1+2n2 ；由①、②两式把n2消去得：n= 2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。

满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

二叉树的实现

对于二叉树的创建，我提供给大家两种思路。初学者建议使用第一种，思路简单。第二种创建方式是利用数组递归式创建。

手动创建

手动创建思路很简单：创建节点，赋值，再根据自己的需要传给它左子树和右子树节点。之后重复上述操作直到树创建完成。
例如：

public class BinaryTree<T> 
{
		private T val;
		private BinaryTree<T> leftBTree;
		private BinaryTree<T> rightBTree;

		public BinaryTree(T val)//传值
		{
			this.val = val;
		}

		public void addRightTree (BinaryTree<T> tree)//添加右子树
		{
			rightBTree = tree;
		}
		
		public void addLeftTree (BinaryTree<T> tree)//添加左子树
		{
			leftBTree = tree;
		}
}
		

		BinaryTree<String> bt1 = new BinaryTree<String>("我帅");
		BinaryTree<String> bt2 = new BinaryTree<String>("我很帅");
		BinaryTree<String> bt3 = new BinaryTree<String>("我长得很帅");
		BinaryTree<String> bt4 = new BinaryTree<String>("我的脸长得很帅");
		//下面以bt1作为root，来进行创建
		bt1.addLeftTree(bt2);//为bt1添加左子树bt2
		bt1.addRightTree(bt3);//为bt1添加右子树bt3
		bt2.addRightTree(bt4);//为bt2添加右子树bt4

创建完之后就是这个样子的：

自动创建（懒人福音）

如果采取这种方式，你将只需要创建一个数组，由于我使用了泛型，你可以使用任何类型的数据的数组完成你想要的效果。再将你需要的数组，和数组中的索引传入到createBTree当中，函数就会用递归的方式自动完成创建。
如下我创建了一个Integer类型的数组：

		Integer[] arr = new Integer[] {1,2,3,null,4};
		BinaryTree<Integer> bt = BinaryTree.createBTree(arr,0);

public static<T> BinaryTree<T> createBTree(T [] arr,int index)
		{
		BinaryTree<T> tree = null;
		if(index<arr.length&&arr[index] != null)
		{
			tree = new BinaryTree<T>(arr[index]);//对当前的树传值
			tree.leftBTree = createBTree(arr,index*2+1);//对左子树递归
			tree.rightBTree = createBTree(arr,index*2+2);//对右子树递归
		}
		return tree;
		}

创建后是这个样子：

删除节点

采用递归删除的方法，传入该树后将其本身和子树全部删除。
接下来我演示删除整个数，以先前的bt1为例子：

bt1.deleteTree();

调用下列函数：

public void deleteTree()
		{
			if(leftBTree != null)leftBTree.deleteTree();//左子树递归
			if(rightBTree != null)rightBTree.deleteTree();//右子树递归
			clearTree();
		}
private void clearTree()
		{	//所有元素赋空
			this.val = null;
			this.leftBTree = null;
			this.rightBTree = null;
		}

内存中清除顺序示意图：

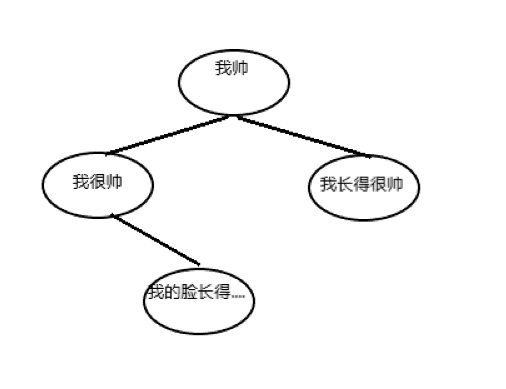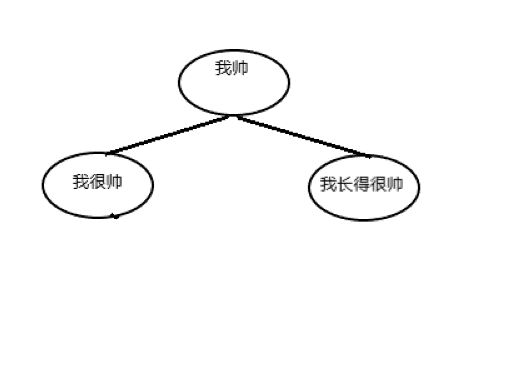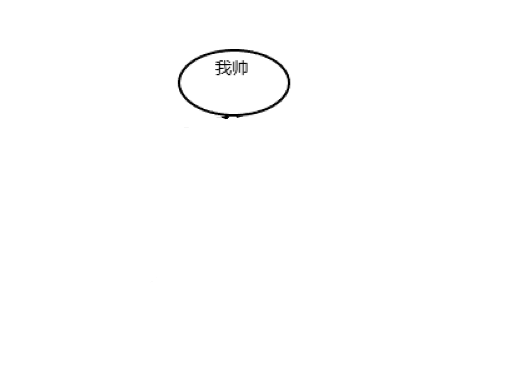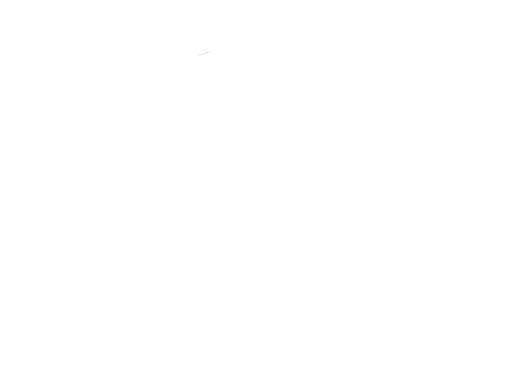
三种基本遍历

依旧是递归思路
注：
T：根
R：右
L：左

前序遍历

顺序：TLR

public void preOrderTraversal()
		{
			System.out.println(val);//根
			if(leftBTree != null)//左
				leftBTree.preOrderTraversal();
			if(rightBTree != null)//右
				rightBTree.preOrderTraversal();
		}

中序遍历

顺序：LTR

public void inOrderTraversal()
		{
			if(leftBTree != null)//左
				leftBTree.inOrderTraversal();
			System.out.println(val);//跟
			if(rightBTree != null)//右
				rightBTree.inOrderTraversal();
		}

后序遍历

顺序：LRT

public void postOrderTraversal()
		{
			if(leftBTree != null)//左
				leftBTree.postOrderTraversal();
			if(rightBTree != null)//右
				rightBTree.postOrderTraversal();
			System.out.println(val);//根
		}

本文完整代码

public class MainFunction {
	public static void main(String[] args)
	{
		Integer[] arr = new Integer[] {1,2,3,4};
		BinaryTree<Integer> bt = BinaryTree.createBTree(arr,0);
		bt.preOrderTraversal();
		bt.inOrderTraversal();
		bt.postOrderTraversal();
		bt.deleteTree();
		BinaryTree<String> bt1 = new BinaryTree<String>("我帅");
		BinaryTree<String> bt2 = new BinaryTree<String>("我很帅");
		BinaryTree<String> bt3 = new BinaryTree<String>("我长得很帅");
		BinaryTree<String> bt4 = new BinaryTree<String>("我的脸长得很帅");
		bt1.addLeftTree(bt2);
		bt1.addRightTree(bt3);
		bt2.addRightTree(bt4);
		bt1.preOrderTraversal();
		bt1.inOrderTraversal();
		bt1.postOrderTraversal();
		bt1.deleteTree();
	}
}

public class BinaryTree<T> 
{
		private T val;
		private BinaryTree<T> leftBTree;
		private BinaryTree<T> rightBTree;
		
		
		public BinaryTree(T val)
		{
			this.val = val;
		}
		
		private void clearTree()
		{
			this.val = null;
			this.leftBTree = null;
			this.rightBTree = null;
		}
		
		public void addRightTree (BinaryTree<T> tree)
		{
			rightBTree = tree;
		}
		
		public void addLeftTree (BinaryTree<T> tree)
		{
			leftBTree = tree;
		}
		
		public void editTree(T val)//编辑函数，可以用于修改数的值
		{
			this.val = val;
		}
		
		public boolean isLeaf()//判断是否为叶节点
		{
			if((val != null)&&(leftBTree == null)&&(rightBTree == null))
				return true;
			return false;
		}
		
		public void deleteTree()
		{
			if(leftBTree != null)leftBTree.deleteTree();
			if(rightBTree != null)rightBTree.deleteTree();
			clearTree();
		}

		public static<T> BinaryTree<T> createBTree(T [] arr,int index)
		{
			BinaryTree<T> tree = null;
			if(index<arr.length&&arr[index] != null)
			{
				tree = new BinaryTree<T>(arr[index]);
				tree.leftBTree = createBTree(arr,index*2+1);
				tree.rightBTree = createBTree(arr,index*2+2);
			}
			return tree;
		}
		
		public void preOrderTraversal()
		{
			System.out.println(val);
			if(leftBTree != null)
				leftBTree.preOrderTraversal();
			if(rightBTree != null)
				rightBTree.preOrderTraversal();
		}
		
		public void inOrderTraversal()
		{
			if(leftBTree != null)
				leftBTree.inOrderTraversal();
			System.out.println(val);
			if(rightBTree != null)
				rightBTree.inOrderTraversal();
		}
		
		public void postOrderTraversal()
		{
			if(leftBTree != null)
				leftBTree.postOrderTraversal();
			if(rightBTree != null)
				rightBTree.postOrderTraversal();
			System.out.println(val);
		}	
		
}

尾言

这就是今天我给大家介绍关于二叉树的全部内容，第二弹我会尽快写完😑😑😑大家稍安勿躁，好好把本文的东西消化好。༼ つ ◕_◕ ༽つ
有什么问题评论区中尽管问我，无特殊情况24小时内回复。大家一起进步嗷