机器学习基础个人笔记（三）

        继续附上前两章的链接

机器学习个人笔记（一）_NanGuai的博客-优快云博客

机器学习个人笔记（二）_NanGuai的博客-优快云博客

目录

逻辑回归

分类问题

假说表示

多类别分类：一对多

---

逻辑回归

分类问题

        在分类问题中，逻辑回归是一种非常流行的学习算法。最简单的是二分类，即预测结果只有两类，例如判断一封电子邮件是否是垃圾邮件；某辆列车是否能准点到达；还有之前讨论过的根据肿瘤大小（虽然现实中不太靠谱）来预测肿瘤是否为良性。

        就以这个为例，我们来看一下下面这幅图。

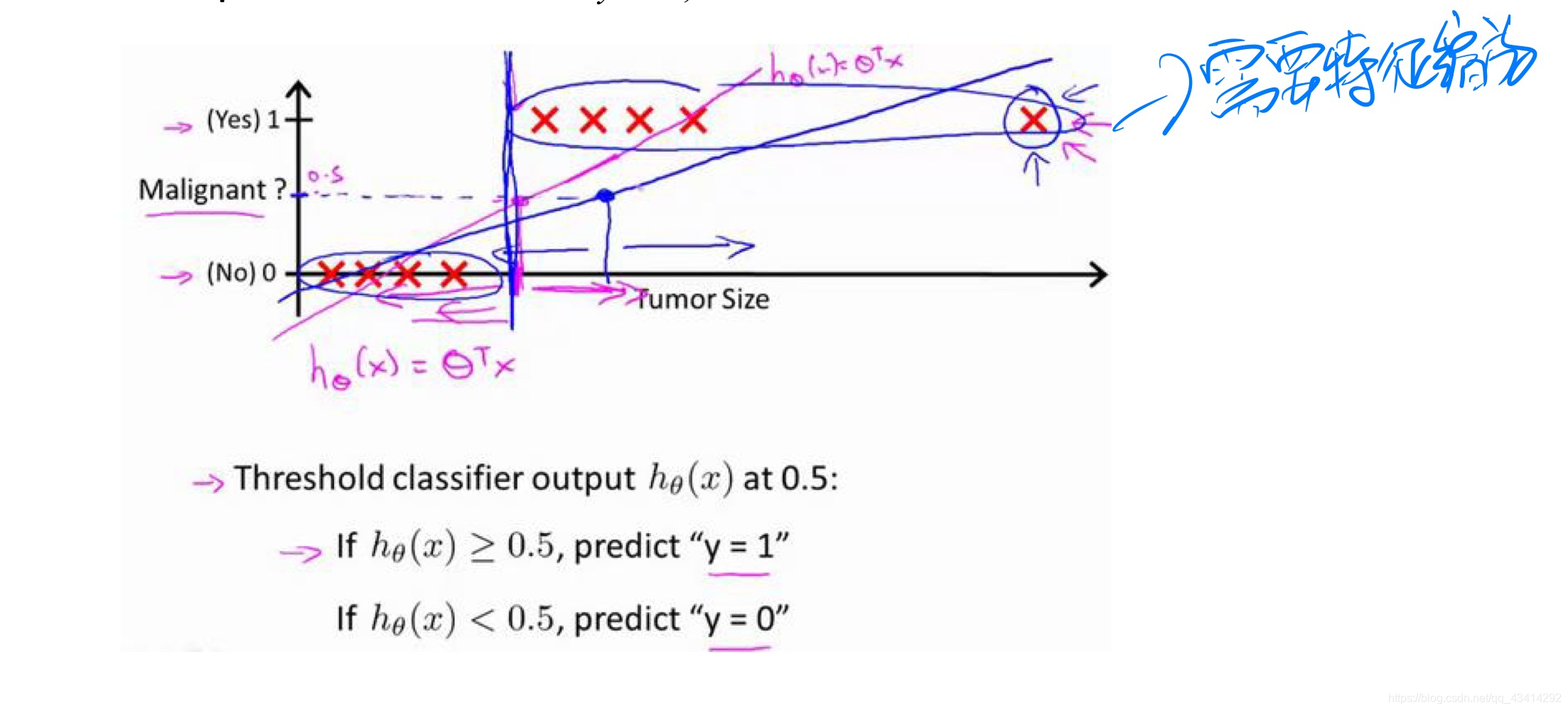
        这是一个二元分类，横轴代表的是肿瘤的大小，竖轴1表示为恶性，0表示为良性。将线性回归应用到这个数据集中，拟合出一条直线（红线），并将分类器输出的阈值设置为0.5，即如果输出的值大于0.5则预测y为1，也就是预测为恶性肿瘤，反之亦然。我们可以看到，所得出来的结果貌似还不错，但是如果我们再加入一个训练样本，也就是那个较大的肿瘤（最右边的那个×），那么最后拟合出来的曲线（蓝线）势必会被影响，现在再看这条曲线，好像已经不太准确了。这里插一句，其实我本人感觉这里非常像特征缩放那里说到的，如果特征的维度相差过大，那么会对最后的结果产生一定的影响。

        在分类问题中，y的取值为1或0，但是如果你采用线性回归的学习算法，函数的输出值就可能远大于1或是远小于0。逻辑回归算法就能很好的解决这个问题，它能让输出一直保持在0到1之间。

假说表示

        需要找到一个满足我们假设或者某个性质的函数，要求这个函数的输出值在0到1之间。此时引入一个新的模型——逻辑回归。假设，其中：X表示特征向量，g表示逻辑函数，公式为:,名为sigmoid函数。

        该函数的图像为：

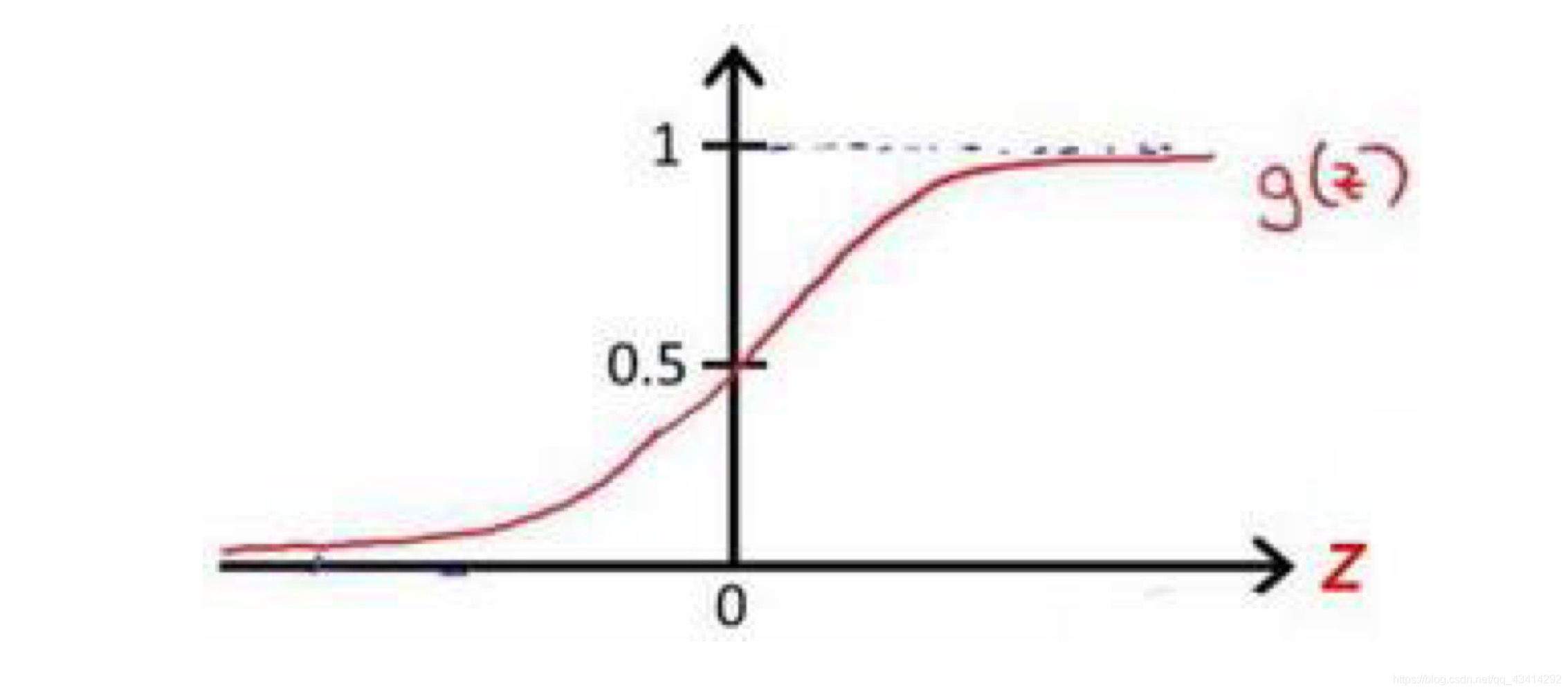
        函数理解：对于给定的z，可以计算出对应的y值，y值表示有多少的概率预测为“1”。

        python代码实现：

import numpy as np
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

多类别分类：一对多

        之前我们所提到的分类问题都是最简单的二分类问题，但生活中不仅仅只存在二分类。比如说人的表情，你可以简单点只分为开心与难过，但是其实人的表情非常复杂，包括生气、开心、难过、害羞等，这便是多分类。

        下面分别是一个二分类和一个多分类（图中为三分类）的数据集。

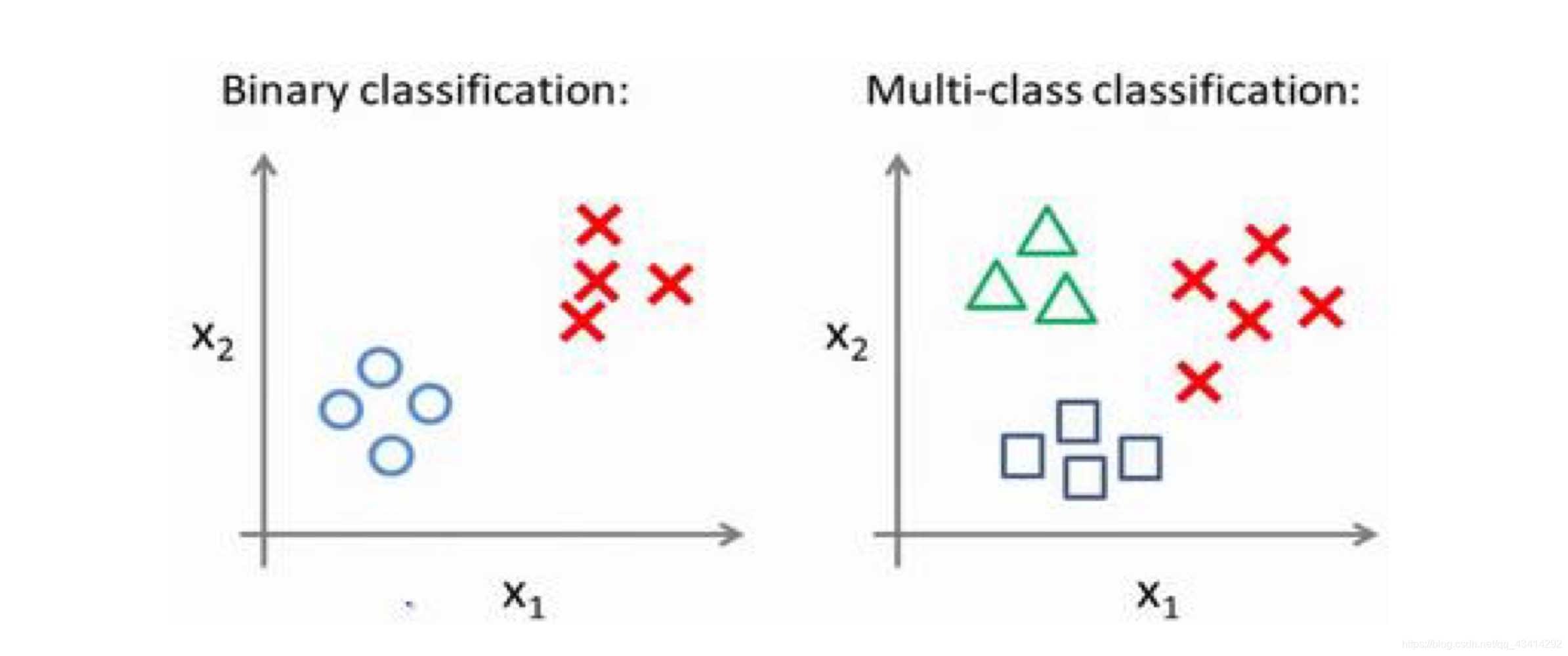
        利用逻辑回归可以进行二元分类，对于第一幅图我们可以将数据集分为两个部分，那在面对多分类的时候该如何将数据集分为多个部分呢？在我的理解当中，多分类其实就是多次二分类求概率最高，接下来看一下具体操作。

        

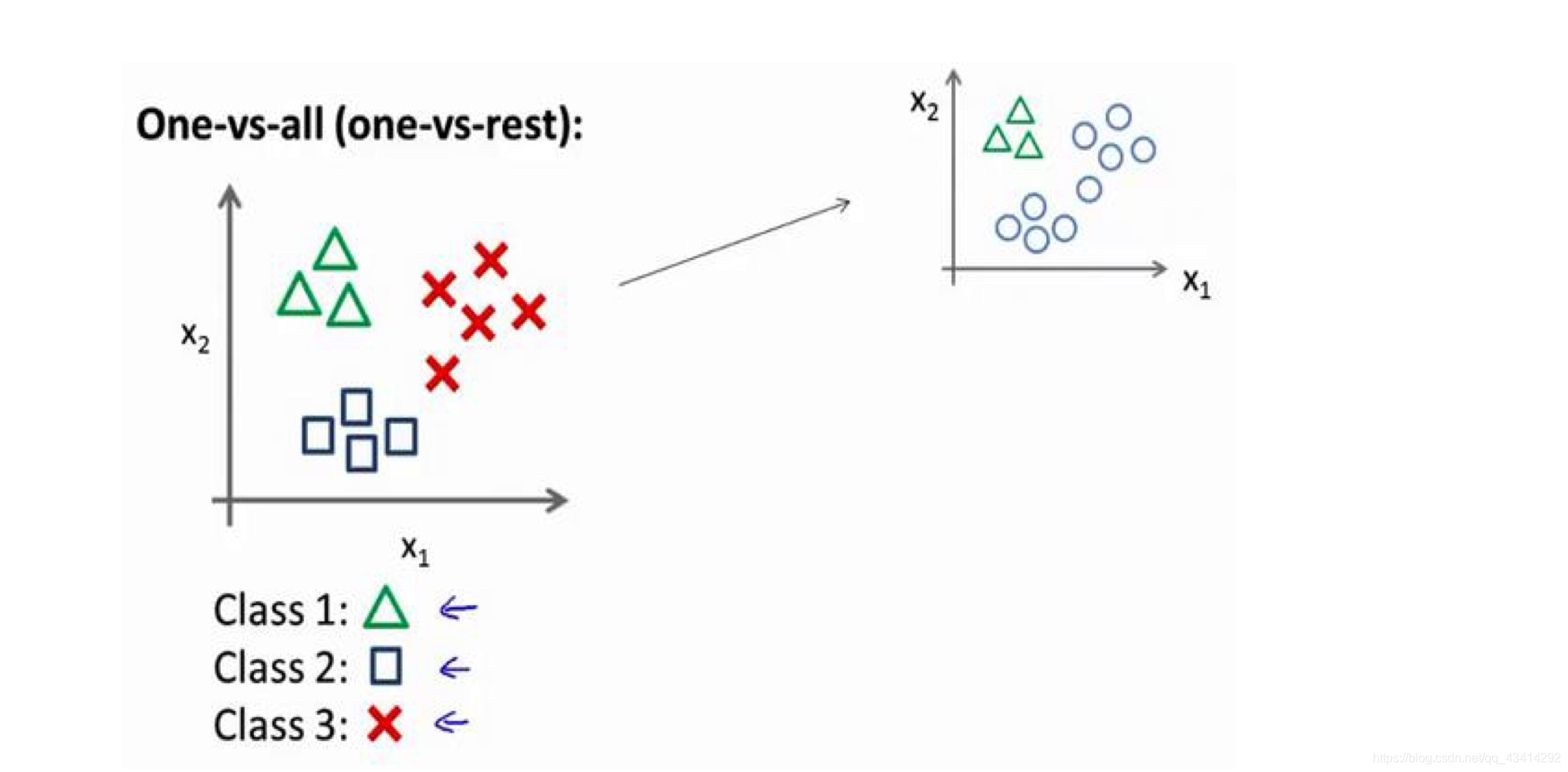
        任选一个类别作为正向类，其余样本作为负向类（本例中将三角形为正向类，正方形和红叉为负向类）构建模型，这个模型记为。类似的操作，将剩下的两个类都各当作一次正向类得到模型和。图示如下：

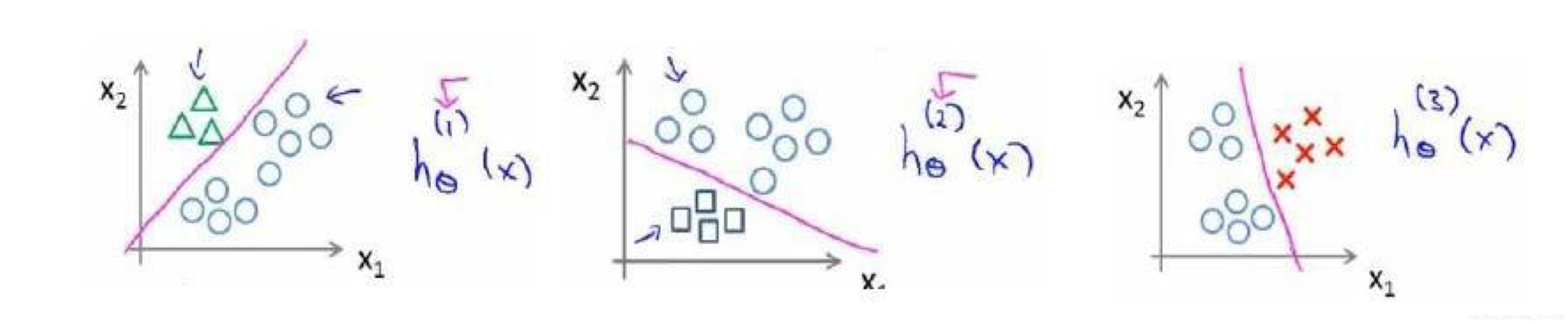
        将三个模型简写为：，当要进行预测时，只需要将预测值输入三个分类器中并取最大i。