字典树

Trie又被称为字典树、前缀树。所谓字典树，顾名思义，就是像字典一样的树，可以通过这棵树快速查找单词。

例如给出一串单词 inn, int, at, age, adv, ant 

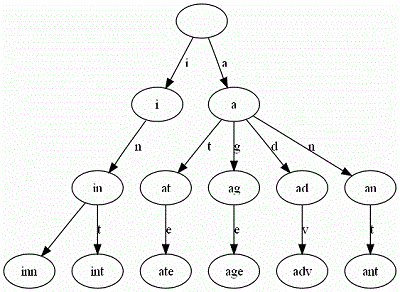
基本性质：

1）根节点不包含字符，除根节点外每一个节点都只包含一个字符。　　

2)   字典树用边表示字母

3）从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。　

4）每个节点的所有子节点包含的字符都不相同，每个节点最多有26个子节点（在单词只包含小写字母的情况下）

5)   有相同前缀的单词公用前缀节点

6)   整棵树的根节点是空的，便于插入和查找

7)   每个单词结束的时候用一个特殊字符表示，那么从根节点到任意一个特殊字符，所经过的边的所有字母表示一个单词

 

1.字典树的插入

对于字典树的插入，我们首先需要维护两个编号。

一种是i,k表示节点对于整棵树的节点编号

一种是j，表示节点i的第j个孩子，这是对于节点i来说

例子：

单词：cat cash app apple aply ok
第一种编号：

首先输入的是cat，所以c,a,t分别是1,2,3,然后输入的是cash，因为c,a是公共前缀，所以c,a跳过，从s开始编，s是4，h是5，然后输入app 此时app的'a'与cash和cat的'a'编号不同

第二种编号：

因为每个节点最多有26个子节点，我们可以按他们的字典序从0-25编号，也就是他们的ASCLL码-a的ASCLL码，此时相同字母的编号相同

因此我们可以构建一个数组trie[i][j]=k,表示编号为i的节点的第j个孩子是编号为k的节点

//对于字符串比较多的要统计个数的，map被卡的情况下，直接用字典树
//很多题都是要用到节点下标来表示某个字符串
const int maxn =2e6+5;//如果是64MB可以开到2e6+5，尽量开大
int tree[maxn][30];//tree[i][j]表示节点i的第j个儿子的节点编号
bool flagg[maxn];//表示以该节点结尾是一个单词
int tot;//总节点数
void insert_(char *str)
{
   int  len=strlen(str);
   int root=0;
   for(int i=0;i<len;i++)
   {
       int id=str[i]-'a';
       if(!tree[root][id]) tree[root][id]=++tot;
       root=tree[root][id];
   }
   flagg[root]=true;
}
bool find_(char *str)//查询操作，按具体要求改动
{
    int len=strlen(str);
    int root=0;
    for(int i=0;i<len;i++)
    {
        int id=str[i]-'a';
        if(!tree[root][id]) return false;
        root=tree[root][id];
    }
    return true;
}
void init()//最后清空，节省时间
{
    for(int i=0;i<=tot;i++)
    {
       flagg[i]=false;
       for(int j=0;j<10;j++)
           tree[i][j]=0;
    }
   tot=0;//RE有可能是这里的问题
}