支持向量机(SVM)
假设函数:
形式

与神经网络的两点区别:
1.代价函数
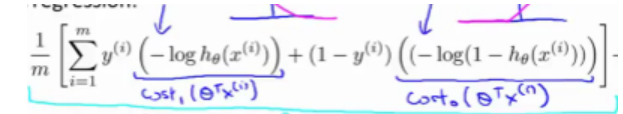
可以从这个对比上看出原来的神经网络是对数形式的sigmoid函数我们将其替换为cost1和cost0,分别意味着预测结果距离1的代价和距离0的代价。
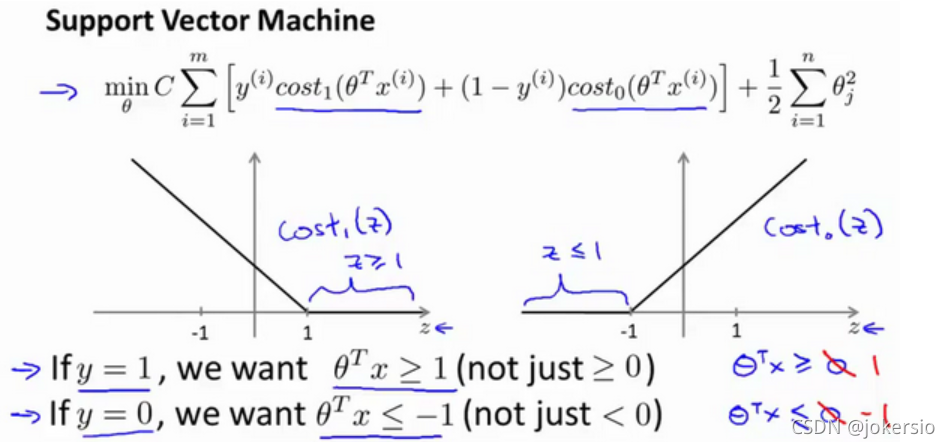
新代价函数图形,当距离足够远时直接令Z=0;
2.C的引入
正则化项前不再拥有参数λλλ,反而是预测项拥有了系数C,我们这里可以把C理解为1/λ1/λ1/λ。
大间距分类器
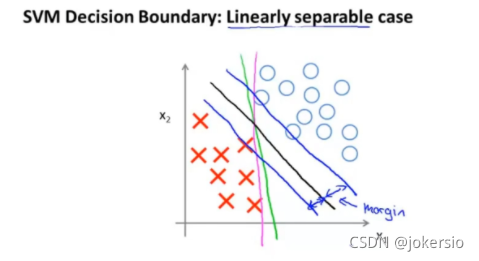
如图的一组正负样本,SVM所做的正式那条黑色的直线,尽力以最大的间距将两组数据分割开来(可以理解为到蓝色的直线的距离)
数学理解

为何能进行大间距分类?
我们将θT∗Xθ^T*XθT∗X看成向量内积的形式,那么其也可以写成P×∣∣θ∣∣P×||θ||P×∣∣θ∣∣的形式,其中P为X在θ方向上的投影,因为我们想要我们的代价函数取最小值,所以我们会令P×∣∣θ∣∣P×||θ||P×∣∣θ∣∣的绝对值尽量大,在θ不变的情况下,即令P的值尽量大
在这个示例里我们会让θ尽量贴近于坐标轴,而分割线则会垂直于坐标轴。
核函数(kernel)
引入
为了解决复杂的非线性分类问题

如图所示,如果想要解决这种问题,用神经网络的方法是将原来的特征进行排列组合,引入大量的多项式比如x12,x2x3x_1^2,x_2x_3x12,x2x3作为新的特征,但是这样会拖慢计算机的运行速度。
在SVM中我们引入了新的构造特征值的方法,即利用核函数。
也可理解为相似函数
给定一个训练样本x,我们利用x的各个特征与我们预先选定的地标(landmarks)l1,l2,l3l_1,l_2,l_3l1,l2,l3的近似程度来选取新的特征。
高斯核函数:
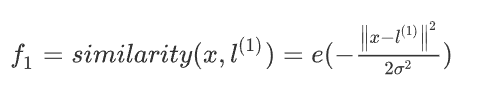
当x与l1l_1l1靠近时,f1f_1f1的值趋近于1
当x与l1l_1l1远离时,f1f_1f1的值趋近于0
实例
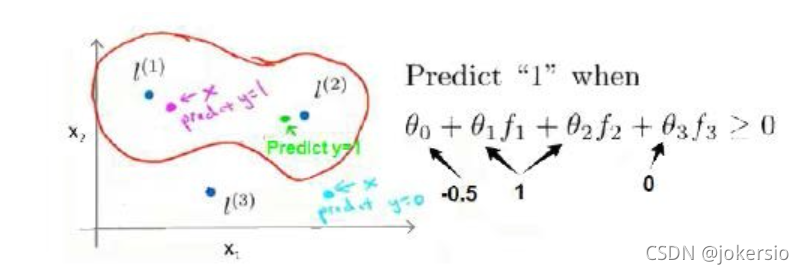
对于如图的模型,假设我们训练出的参数如上,那最终我们会形成这样的分类效果。
特征点的选取
若训练集有m个样本,则选取m个特征点
对每一个样本都对其他所有点取高斯核函数,那么每一个点都可以形成一个这样的m维特征向量
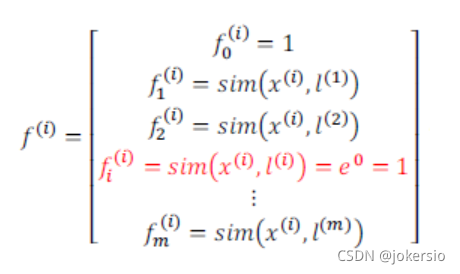
方程进化
我们的代价函数也会相应地变成这样:
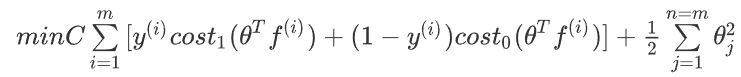
这时我们的判断就是当θTf(i)>0θ^Tf^{(i)}>0θTf(i)>0时,predict y=1
当θTf(i)<0θ^Tf^{(i)}<0θTf(i)<0时,predict y=0
有时我们也会用θT∗M∗θθ^T*M*θθT∗M∗θ来代替θ2θ^2θ2,其中M的值取决于核函数
这样做的目的是简化计算,提高运行时的速度
参数选择
因为C=1/λC=1/λC=1/λ
所以C过大,意味着λ偏小,可能导致高方差,过拟合
所以C过大,意味着λ偏大,可能导致高偏差,欠拟合
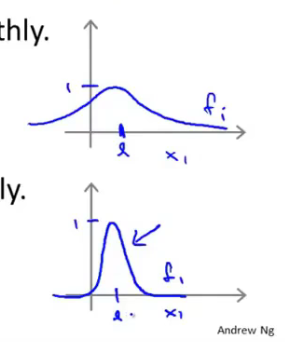
σ的大小和核函数的平滑程度有关
而σ过大,意味着高偏差,欠拟合
而σ过小,意味着高方差,过拟合
参考正态分布图像
线性核函数
即不适用核函数的情况‘
因为它的作用是仅仅提供一个线性分类器,因此得名
适用于有大量特征值和很少数据集的情况
应用
多类分类问题
可以应用one vs all的方法,也可以直接调用SVM软件库里的多分类器(一般会有)
需要做的事
- 确定参数C
- 选择恰当的核函数(一般是高斯或线性)
算法选择
n为特征数,m为训练样本数。
SVM的速度主要取决于m的大小,逻辑回归速度取决于n的大小
-
n>>m,即训练集数据量不够支持我们训练一个复杂的非线性模型
我们选用逻辑回归模型或者不带核函数的支持向量机。
-
如果n较小,而且m大小中等
例如n在 1-1000 之间,而m在10-10000之间
使用高斯核函数的支持向量机。
-
如果n较小,而m较大,例如n在1-1000之间,而m大于50000
则使用支持向量机会非常慢,解决方案是创造、增加更多的特征
然后使用逻辑回归或不带核函数的支持向量机。
另这些情况使用训练得当的神经网络都会得到恰当的结果
但是比如上面第二种种情况SVM的速度会远快于神经网络





 本文深入探讨支持向量机(SVM)的原理,包括其与神经网络的区别,如代价函数的转换和C参数的引入,以及如何实现大间距分类。介绍了核函数的概念,特别是高斯核函数的作用,用于解决非线性分类问题。此外,讨论了参数选择对模型性能的影响,如C和σ的选择,并提供了不同场景下选择SVM或逻辑回归的指导。最后,SVM在多类分类问题中的应用以及如何确定合适的参数也被提及。
本文深入探讨支持向量机(SVM)的原理,包括其与神经网络的区别,如代价函数的转换和C参数的引入,以及如何实现大间距分类。介绍了核函数的概念,特别是高斯核函数的作用,用于解决非线性分类问题。此外,讨论了参数选择对模型性能的影响,如C和σ的选择,并提供了不同场景下选择SVM或逻辑回归的指导。最后,SVM在多类分类问题中的应用以及如何确定合适的参数也被提及。
















 5879
5879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








